Задания для самостоятельной работы
1. Найти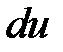 
и 
, если
а) 
; б) 
;
в) 
; г) 
д) 
; е) 
.
ж) 
.; з) 
;
2. Вычислить приближенно
а) 
; б) 
; в) 
.
Производная по направлению. Градиент.
Пусть функция 
дифференцируема в области 
и пусть в этой области задано некоторое направление 
. Производная функции по направлению 
вычисляется по формуле
(1)
Скорость наибольшего роста функции в данной точке (по величине и направлению) определяется вектором, который обозначается символом 
и называется градиентом функции:
(2)
Пример 1. Найти производную функции 
в точке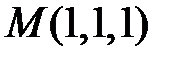 
в направлении 
. Чему равна величина градиента функции в этой точке?
Решение. Чтобы воспользоваться формулой (1), подсчитаем частные производные в точке 
:
Значит, производная функции в заданном направлении равна
.
В соответствии с формулой (2) запишем градиент функции в точке 
– вектор
Величина градиента (модуль вектора) равна 
. ☻
Пример 2. Найти производную функции 
в точке 
в направлении, составляющем угол 
с положительным направлением оси 
.
|
|
|
Решение. Подсчитаем сначала частные производные в точке :
.
Найдем направляющие косинусы:
.
По формуле (1) запишем
. ☻
Пример 3. Для функции 
определить угол между градиентами в точках 
и 
.
Решение. Подсчитаем сначала частные производные:
Теперь можем записать градиент функции в точках 
и 
:
,
.
Очевидно, эти векторы ортогональны – их скалярное произведение равно нулю: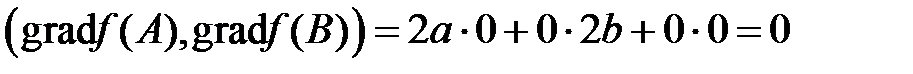 
. Значит, угол между градиентами равен 
. ☻
Задания для самостоятельной работы.
1. Найти производную функции 
в точке 
в направлении, идущем от этой точки к точке 
.
2. Найти производную функции 
в точке 
в направлении биссектрисы первого координатного угла.
3. Найти производную функции 
в точке 
в направлении, идущем от этой точки к началу координат.
4. 
. Найти 
в точке 
.
5. 
. Найти в точке 
.
6. 
. Найти в точке 
.
7. 
. Найти угол между градиентами этой функции в точках 
и 
.
8. Даны функции 
и 
. Найти угол между градиентами этих функций в точке .
9. Найти точку, в которой градиент функции 
равен 
.
10. Найти точки, в которых модуль градиента функции 
равен 2.
11. Найти наибольшую крутизну подъема поверхности 
в точке 
.
|
|
|
12. Найти наибольшую крутизну подъема поверхности 
в точке 
.
Экстремумы функций многих переменных
Для функций многих переменных термины «максимум функции» и «минимум функции» имеют тот же смысл, что и для функций одной переменной, а именно: этими терминами обозначаются наибольшее или соответственно наименьшее значение функции в точке 
по сравнению со значениями функции в точках, соседних с . Дадим строгое определение.
Определение. Пусть функция 
определена в области 
. Точка 
называется точкой максимума (соответственно, минимума), если существует такая окрестность 
точки , что для всех 
выполняется неравенство
.
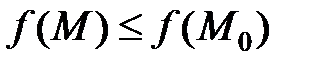
Здесь
, 
,
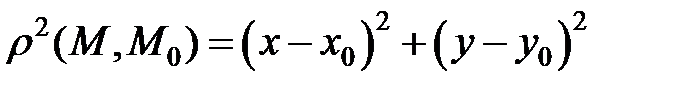
Точки максимума и минимума функции называются точками экстремума.
Теорема 1. (Необходимые условия экстремума). Пусть функция определена в некоторой окрестности точки . Если – точка экстремума функции и функция дифференцируема в этой точке, то
(1)
Точки, в которых имеет место равенство (1), называются стационарными.
Дифференцируемая функция может и не иметь экстремума в стационарной точке. Иначе говоря, необходимые условия экстремума, данные в теореме 1, не являются условиями, достаточными для наличия экстремума у функции в точке . Это подтверждает следующий пример.
|
|
|
Пример 1. Убедиться, что функция 
не имеет экстремума в стационарной точке.
Решение. Найдем стационарные точки функции. Для этого сначала подсчитаем частные производные:
и приравняем их к нулю
при 
.
Итак, найдена стационарная точка 
. Значение функции в точке 
равно 0. но в сколь угодно малой окрестности точки 
функция принимает как положительные, так и отрицательные значения. Действительно, если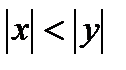 
, то 
, если же 
, то 
. Следовательно, в стационарной точке функция экстремума не имеет. Поверхность, определяемая уравнением – гиперболический параболоид – имеет в окрестности начала координат седлообразную форму.☻
Чтобы установить, действительно ли рассматриваемая функция имеет в стационарной точке экстремум, естественно обратиться к рассмотрению разности 
. Если для всех точек 
из некоторой окрестности точки справедливо неравенство 
, то в точке функция 
имеет минимум (максимум).
Разложим разность 
по формуле Тейлора с остаточным членом в форме Пеано, ограничиваясь двумя членами. Естественно при этом предположить, что функция дважды дифференцируема в окрестности точки . Так как точка предполагается стационарной, то 
, тогда интересующая нас разность запишется в виде
|
|
|
, 
Таким образом, знак приращения 
совпадает со знаком второго дифференциала функции в точке .
Второй дифференциал функции в точке – это квадратичная форма от переменных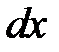 
, 
. От свойств квадратичной формы зависит, сохраняет ли разность определенный знак в некоторой окрестности точки , т.е. имеет ли функция экстремум в точке .
Напомним соответствующие определения.
Определение. Квадратичная форма
, 
(2)
называется положительно (отрицательно) определенной, если 
( 
) для любой точки 
, 
.
Теорема 2. (Достаточные условия экстремума). Пусть функция определена и имеет непрерывные производные 2-го порядка в некоторой окрестности точки , а является стационарной точкой функции. И пусть квадратичная форма от переменных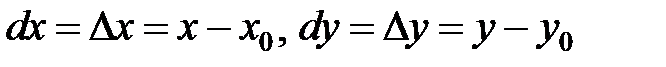 
(3)
является положительно определенной (отрицательно определенной). Тогда
и является точкой минимума (соответственно максимума). Если же квадратичная форма (2) является знакопеременной, то разность не сохраняет знак в окрестности точки – экстремума нет.
Квадратичная форма, являющаяся положительно или отрицательно определенной, называется знакоопределенной.
Квадратичная форма 
называется знаконеопределенной (знакопеременной), есл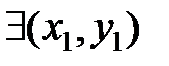и 
и 
такие, что 
, а 
.
Как выяснить, будет ли квадратичная форма (3) знакоопределенной? Ответ на этот вопрос дает теорема
Критерий Сильвестра. Для того, чтобы квадратичная форма (2) с матрицей 
(у которой ) была положительно определена, необходимо и достаточно, чтобы угловые миноры матрицы 
были положительными:
, 
.
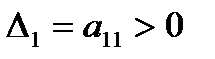Для того, чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы знаки угловых миноров чередовались, начиная с отрицательного, т.е.
, 
. ☻
Для функций двух переменных матрица соответствующей квадратичной формы (2-го дифференциала) имеет вид (производные берутся в точке ):
Сформулируем достаточные условия экстремума для случая функции двух переменных.
Теорема 3. Если в стационарной точке 
выполняется неравенство
, (4)
то функция 
имеет в экстремум, а именно: минимум в случае, когда 
; максимум, когда 
.
Пример 2. Найти экстремумы функции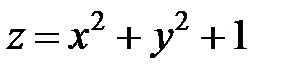 
.
Решение. Найдем стационарные точки, приравнивая нулю частные производные:
при 
;
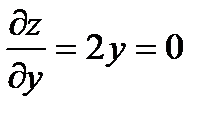при 
.
Итак, есть одна стационарная точка .
Вычислим 
, 
, 
и составим матрицу
.
Неравенство (4) выполняется: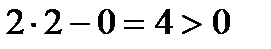 
, т.е. данная функция имеет в начале координат экстремум, а именно, минимум так как 
; 
. Поверхность, определяемая уравнением 
– это параболоид вращения с вершиной в точке (0,0,1). ☻
Пример 3. Исследовать на экстремум функцию 
Решение. Подсчитаем частные производные
, 
Приравниваем производные нулю (необходимое условие экстремума):
Получили единственную стационарную точку 
– точку возможного экстремума. Чтобы выяснить, действительно ли имеется экстремум в точке 
, обратимся к достаточным условиям. Для этого подсчитаем
, 
, 
и составим матрицу
Находим угловые миноры этой матрицы:
, 
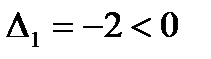В силу достаточного условия в точке имеется максимум. Находим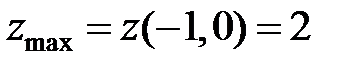 
.☻
Пример 3. Исследовать на экстремум функцию 
Решение. Найдем частные производные и приравняем их к нулю (необходимое условие экстремума)
.
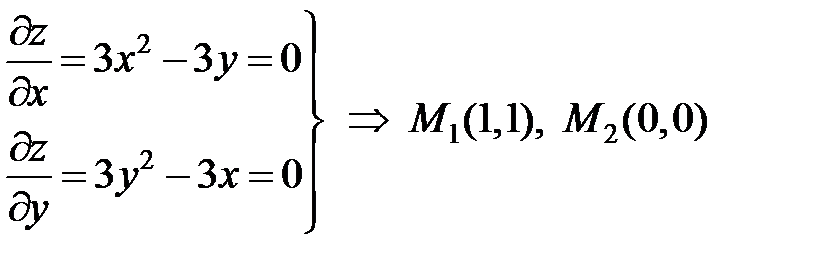Получили две стационарные точки.
Проверим достаточные условия для точки 
. Для этого подсчитаем
, 
, 
Составляем для точки матрицу 
и находим угловые миноры: 
, 
. В силу достаточного условия в точке 
имеется минимум. Находим 
.
Посмотрим, есть ли экстремум в точке 
. Подсчитаем
, 
, 
.
Составляем для точки матрицу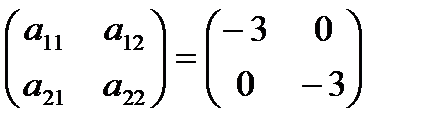 
, для нее 
, 
. Достаточное условие экстремума не выполнено – в точке заданная функция экстремума не имеет.☻
Пример 4. Убедиться, что функция 
в точке 
имеет максимум.
Решение. Проверим сначала, является ли точка стационарной для заданной функции. Для этого подсчитаем
Равенство нулю производных в точке убеждает нас, что это действительно стационарная точка. Является ли стационарная точка точкой экстремума? Чтобы воспользоваться достаточными условиями экстремума, подсчитаем
, 
, 
Составим матрицу 
. Ее угловые миноры 
, 
, поэтому в точке имеется экстремум, а именно, максимум. Найдем 
.
Дата добавления: 2020-04-25; просмотров: 84; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!