Задания для самостоятельной работы.
Частные производные
Пусть в области 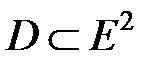 задана функция
задана функция  ;
;  . Придадим независимым переменным
. Придадим независимым переменным  приращения
приращения  соответственно так чтобы точка
соответственно так чтобы точка  .
.
Назовём полным приращением функции  в точке
в точке  разность
разность 
 ,
,  .
.
Наряду с полным приращением функции рассматривают частные приращения. Зафиксируем аргумент  и придадим приращение
и придадим приращение 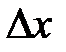 аргументу
аргументу  . Частное приращение функции
. Частное приращение функции  по переменной
по переменной  – это разность
– это разность
 .
.
Если существует  , то он называется частной производной функции
, то он называется частной производной функции  по переменной
по переменной  в точке
в точке  и обозначается одним из символов
и обозначается одним из символов  :
:
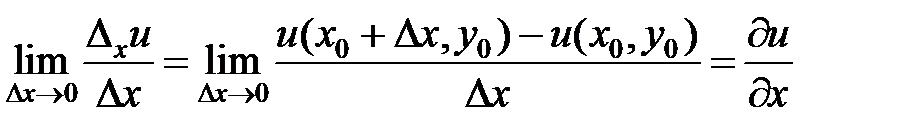
Таким образом, при вычислении частной производной функции  по переменной
по переменной  у этой функции фиксируют переменную
у этой функции фиксируют переменную 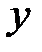 , при этом получают функцию только одной переменной
, при этом получают функцию только одной переменной  , для которой и определяют первую производную.
, для которой и определяют первую производную.
Аналогично определяется частное приращение функции  по переменной
по переменной 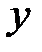 – это разность
– это разность
 .
.
Если существует  , то он называется частной производной функции
, то он называется частной производной функции  по переменной
по переменной 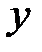 в точке
в точке  и обозначается одним из символов
и обозначается одним из символов  :
:

При вычислении частных производных функции трёх и более переменных  фиксируют все переменные, кроме одной, и дифференцируют полученную функцию одной переменной.
фиксируют все переменные, кроме одной, и дифференцируют полученную функцию одной переменной.
Частные производные вычисляются по тем же правилам, что и обыкновенные.
Пример 1. Найти частные производные по всем переменным следующих функций:
а)  , б)
, б)  , в)
, в) 
Решение . а) фиксируем 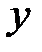 и дифференцируем функцию
и дифференцируем функцию  по переменной
по переменной  :
:
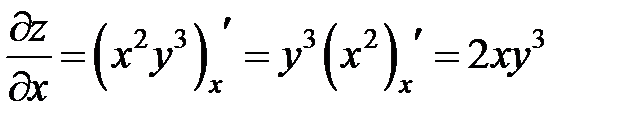 ;
;
фиксируем  и дифференцируем функцию
и дифференцируем функцию  по переменной
по переменной  :
:
|
|
|
 .
.
б) Дифференцируем функцию  по переменной
по переменной  при фиксированных
при фиксированных  и
и  :
:
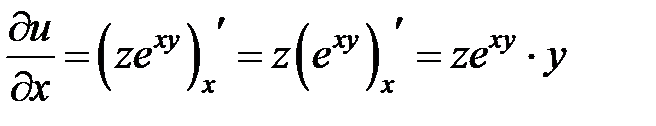 .
.
Дифференцируем функцию  по переменной
по переменной  при фиксированных
при фиксированных  и
и  :
:
 .
.
Наконец, фиксируем  и
и  и дифференцируем функцию
и дифференцируем функцию  по переменной
по переменной  :
:
 .
.
в)  ,
, 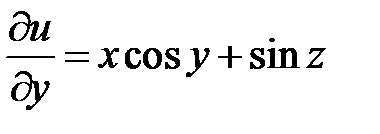 ,
,  . ☻
. ☻
Задания для самостоятельной работы.
Найти частные производные данных функций по каждой из независимых переменных (  - переменные):
- переменные):
1)  2)
2) 
3)  (
(  - постоянные) 4)
- постоянные) 4) 
5)  6)
6) 
7)  8)
8) 
9)  10)
10) 
11)  12)
12) 
13)  14)
14) 
15)  16)
16) 
17)  18)
18) 
19)  20)
20) 
21)  22)
22) 
23)  24)
24) 
25)  26)
26) 
27)  28)
28) 
29)  30)
30) 
|
|
|
31)  32)
32) 
33) 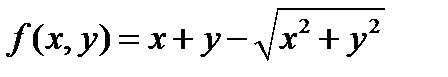 в точке (3,4) 34)
в точке (3,4) 34) 
35)  в точке (1,2) 35)
в точке (1,2) 35) 
37)  37)
37) 
Старшие производные
Так же, как и для одной переменной, определяем старшие производные функции многих переменных:
 ;
;  и т.д.
и т.д.
Такие производные для функций многих переменных называются «чистыми». Если же после взятия первой производной по  мы хотим результат
мы хотим результат 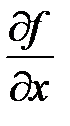 продифференцировать по другой переменной, например, по
продифференцировать по другой переменной, например, по  , то получим «смешанную» производную
, то получим «смешанную» производную

Ясно, что так можно построить старшие производные любого порядка по всем переменным.
Пример 1. Найти частные производные 1-го и 2-го порядка от функции
 .
.
Решение. Фиксируем  и дифференцируем функцию по
и дифференцируем функцию по  :
:
 .
.
Фиксируем  и дифференцируем по
и дифференцируем по  :
:
 .
.
Далее находим последовательно




Обращаем внимание на полученный результат:
 . ☻
. ☻
Смешанные производные  и
и  , вообще говоря, не равны. Однако справедливо утверждение, которым обычно пользуются:
, вообще говоря, не равны. Однако справедливо утверждение, которым обычно пользуются:
Теорема. Если частные производные функции  существуют в окрестности точки
существуют в окрестности точки 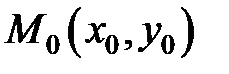 и непрерывны в точке
и непрерывны в точке  , то вторые смешанные производные не зависят от порядка вычисления.
, то вторые смешанные производные не зависят от порядка вычисления.
Аналогичное утверждение справедливо и для смешанных производных  -го порядка.
-го порядка.
|
|
|
Задания для самостоятельной работы.
1. Убедиться, что  , если а)
, если а)  ;
;
б)  ; в)
; в) 
2.  ;
; 
5. 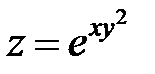 ;
;  6.
6.  ;
; 
7.  ;
;  8.
8.  ;
; 
9.  ; убедиться, что
; убедиться, что  и что
и что  .
.
10.. Показать, что 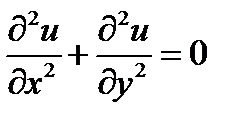 , если
, если
а)  ; б)
; б) 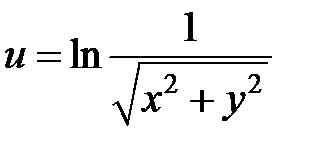
11.  . Показать, что
. Показать, что  .
.
12.  . Показать, что
. Показать, что  , каковы бы ни были дважды дифференцируемые функции
, каковы бы ни были дважды дифференцируемые функции  .
.
13.  . Проверить, что
. Проверить, что  (
( 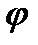 и
и  – дважды дифференцируемые функции).
– дважды дифференцируемые функции).
14.  . Показать, что
. Показать, что  (
( 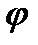 – дифференцируемая функция).
– дифференцируемая функция).
15.  . Показать, что
. Показать, что  (
( 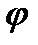 и
и  – дважды дифференцируемые функции).
– дважды дифференцируемые функции).
16.  . Показать, что
. Показать, что  .
.
17.  . Показать, что
. Показать, что  .
.
Дифференциал функции
Определение. Функция  дифференцируема в точке
дифференцируема в точке 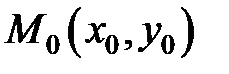 , если её полное приращение в окрестности этой точки представимо в виде
, если её полное приращение в окрестности этой точки представимо в виде
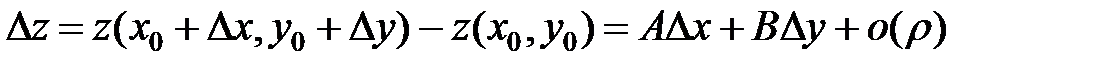 ,
,
где  и
и  - константы, не зависящие от
- константы, не зависящие от  .
.
Если функция  дифференцируема в точке
дифференцируема в точке 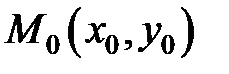 , то
, то  . Обратное, вообще говоря, неверно. В отличие от функций одной переменной, для функций многих переменных из существования в заданной точке первых частных производных не следует дифференцируемость функции по совокупности переменных.
. Обратное, вообще говоря, неверно. В отличие от функций одной переменной, для функций многих переменных из существования в заданной точке первых частных производных не следует дифференцируемость функции по совокупности переменных.
|
|
|
Теорема (достаточное условие дифференцируемости функции двух переменных). Если у функции  частные производные
частные производные  ,
,  существуют в окрестности точки
существуют в окрестности точки 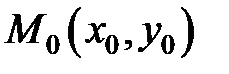 и непрерывны в самой точке
и непрерывны в самой точке  , то функция
, то функция  дифференцируема в этой точке.
дифференцируема в этой точке.
В случае дифференцируемости функции главная линейная часть её приращения  называется первым дифференциалом:
называется первым дифференциалом:
 ,
,  .
.
Пример 1. Найти  для функции
для функции  .
.
Решение. Находим частные производные
 ,
,
 .
.
Первый дифференциал примет вид
 .☻
.☻
Аналогично определяется первый дифференциал функции трех переменных:
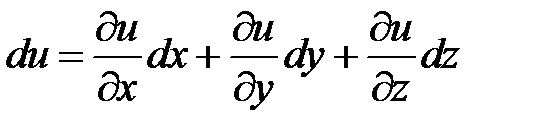 .
.
Пример 2. Найти  для функции
для функции  .
.
Решение . Вычислим
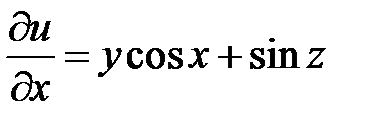 ,
,  ,
,  .
.
Первый дифференциал примет вид:
 . ☻
. ☻
Заменяя полное приращение функции  ее дифференциалом
ее дифференциалом  , получим приближенную формулу (с точностью до
, получим приближенную формулу (с точностью до  :
:
 .
.
Пример 3. Вычислить приближенно 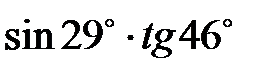 .
.
Решение. Рассмотрим функцию  . В качестве начальной точки возьмём
. В качестве начальной точки возьмём  , тогда у нас
, тогда у нас  .
.
Подсчитаем  . Запишем первый дифференциал в точке
. Запишем первый дифференциал в точке  :
:  .
.
Теперь  . ☻
. ☻
Дифференциалы более высокого порядка от функции  определяются по индукции
определяются по индукции

Для вычисления старших дифференциалов удобно пользоваться символической формулой

С учетом равенства непрерывных смешанных производных при использовании символической формулы для дифференциала  -порядка применяют формулу бинома Ньютона.
-порядка применяют формулу бинома Ньютона.
Например, при  получаем:
получаем:

Аналогично определяются формулы для дифференциалов более высокого порядка от функции 3-х переменных

Пример 4. Найти второй дифференциал для функции  .
.
Решение. Записываем формулу для второго дифференциала
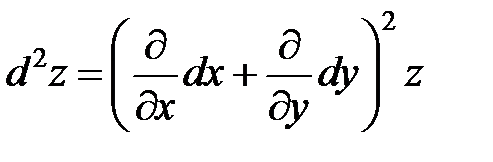
 .
.
Остается подсчитать все производные второго порядка.
Сначала находим первые производные: 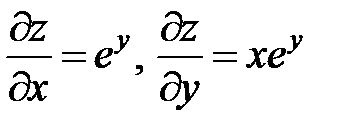 .
.
Подсчитаем вторые производные:  .
.
Следовательно,  . ☻
. ☻
Дата добавления: 2020-04-25; просмотров: 87; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
