Без подписи документ действителен 8 часов после распечатки. Дата и время распечатки: 01.09.2016, 17:07
Стр. 12 из 67


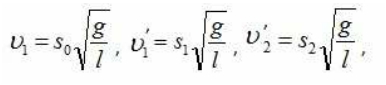



подвеса. Отведя один из шаров (например, большей массы) в сторону и отпустив его, можно
произвести прямой (центральный) удар шаров.
Если до столкновения один из шаров покоился υ 2 =0, то выражение закона сохранения импульса упростится. При прямом ударе оба шара после столкновения движутся по одной прямой, поэтому от векторной формы записи закона
сохранения импульса можно перейти к алгебраической и учитывая, что после столкновения оба шара движутся в одном направлении, получим:
m1∙υ 1= m1∙υ ′ 1 + m2∙υ ′ 2
Для определения скорости первого шара υ 1 до удара и
скоростей шаров υ ′ 1 и υ ′ 2 после удара воспользуемся законом сохранения механической энергии. Потенциальная энергия шара в положении максимального отклонения равняется его
кинетической энергии при ударе , отсюда .
Высоту подъёма шара можно определить по его максимальному отклонению s от положения равновесия (рис. а).
Треугольник АВС прямоугольный (опирается на диаметр). Катет АВ является средней пропорциональной величиной между гипотенузой АС=2 l и своей проекцией на гипотенузу АD (рис.б):
АВ2=АС·AD то есть , откуда . Следовательно,
величины скоростей можно выразить так: где S0,
|
|
|
S1 - максимальные отклонения первого шара до и после удара; S2 - максимальное отклонение второго шара после удара. Запишем уравнение закона сохранения через выражения
скоростей: или m1∙S0= m1∙S1 + m2∙S2. Таким образом,
проверка закона сохранения импульса в данной работе сводится к проверке справедливости
последнего уравнения.
При малых углах отклонения шара от положения равновесия S0, S1 и S2 можно заменить соответствующими величинами, отсчитанными по горизонтальной шкале.
Инструкция по выполнению лабораторной работы
1. Соберите установку по рисунку.
2. Подготовьте в тетради таблицу для записи результатов измерений и вычислений:
| № | m 1, г | m 2, г | S 0, мм | S 1, мм | S 2, мм | m 1 ∙S 0 , г∙мм/с | m 1 ∙S 1 , г∙мм/с | m 2 ∙S 2 , г∙мм/с | m 1 ∙S 1 + m 2 ∙S 2 , г ∙мм/с |
| 1. | |||||||||
| 2. |
3. Определите массы шаров m1 и m2. Запишите их результат в таблицу.
|
|
|
4. Отрегулируйте подвеску шаров так, чтобы их центры и точка касания находились на
одной горизонтальной линии.
5. Отклоните шар большей массы на 5 см от положения равновесия (S0) и затем отпустите его. Заметьте максимальное отклонение этого шара после удара (S1). Повторите опыт 5 раз и найдите среднее значение отклонения S1ср. Запишите его в таблицу (S1).
Версия: 1.0
Без подписи документ действителен 8 часов после распечатки. Дата и время распечатки: 01.09.2016, 17:07
Стр. 13 из 67
6. Повторите опыт 5, но теперь заметьте после удара максимальное отклонение шара с меньшей массой (S2). Повторите опыт 5 раз, и найдите среднее значение отклонения S2ср. Запишите его в таблицу (S2).
7. Отклоните шар большей массы на 8 см от положения равновесия (S0) и затем отпустите его. Заметьте максимальное отклонение этого шара после удара (S1). Повторите опыт 5 раз и найдите среднее значение отклонения S1ср. Запишите его в таблицу (S1).
8. Повторите опыт 7, но теперь заметьте после удара максимальное отклонение шара с меньшей массой (S2). Повторите опыт 5 раз, и найдите среднее значение отклонения S2ср. Запишите его в таблицу (S2).
9. Используя значения S0, S1 и S2, вычислите импульс шара до удара m1∙S0 и сумму импульсов шаров после удара m1∙S1 + m2∙S2 и внесите в таблицу их результаты.
|
|
|
10. Сравните импульс шара до удара с суммой импульсов шаров после удара.
11. Исходя из цели работы, запишите вывод и ответьте на контрольные вопросы.
Контрольные вопросы
1. Что такое импульс материальной точки? По какой формуле он находится?
2. Импульс – величина векторная или скалярная?
3. Запишите формулу и формулировку закона сохранения импульса?
4. Выполняется ли закон сохранения импульса при распаде тела?
5. Какое движение называется реактивным?
6. Выполняется ли закон сохранения импульса при реактивном движении?
Дата добавления: 2020-04-25; просмотров: 267; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
