Проверка генераторов равномерно распределенных псевдослучайных чисел

Лабораторная работа № 1

Анализ и генерация случайных чисел. Основы имитационного моделирования

 

Цель работы: Изучение основных характеристик случайных величин на базе теории вероятностей и математической статистики; изучение и программирование способов получения псевдослучайных чисел.

 

Теоретическая часть

 

Основные понятия и характеристики стохастического процесса

1. Вероятность - мера возможности осуществления результата. Формально это функция Р(х), которая ставит в соответствие результатам некоторые вещественные числа и удовлетворяет аксиомам:

1. 0£Р(х)£1, для любого результата х,

2. Р(s) = 1, где s – пространство выборки,

3. если х₁ , х₂ , х₃ – взаимоисключающие результаты, то вероятность их появления равна сумме вероятностей появления каждого из х_i, то есть P(х₁ È х₂ È х₃ ...) = Р(х₁)+Р(х₂)+P(x₃)+...

2. Случайной величиной называется функция, которая ставит в соответствие каждому результату из пространства выборки некоторое вещественное число.

Случайные величины, имеющие конечное или счетное множество значений, называются дискретными: а если они имеют континуум значений, то являются непрерывными случайными величинами.

3. Вероятностное распределение представляет собой некоторое правило задания вероятности для каждого из всех возможных значений случайной переменной.

Вероятностное распределение характеризуется функциейвероятности р(х) и функцией распределения F(x), Функция вероятности устанавливает конкретную вероятность того, что случайная переменная Х принимает значение х_i; функция, распределения определяет вероятность того, что случайная величина X примет значение меньше заданного х.

Для дискретной случайной величины эти характеристики определяются следующим образом:

· р(х_i) = Р( Х = х_i) со следующими ограничениями: 

o

o

 

· F(x) = P( X < x ) со следующими свойствами:

o

o

 

Функция распределения и функция вероятностей связаны следующим образом:

Для непрерывных случайных величин функция вероятности заменяется на непрерывную функций плотности вероятности f(x), определяемую как:

Функция распределения:

4. Математическоеожидание - взвешенная по вероятности средняя величина всех возможных значений X, определяющая меру центральности распределения.

·  для дискретнойX

·  если Х непрерывна.

5. Математическое ожидание Хⁿ называется n -м моментом случайной переменной и определяется следующим образом:

·  для дискретнойX

·  если Х непрерывна.

Вариациейn -го момента называется n-й момент среднего: .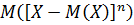

6. Дисперсией случайной переменной называется второй момент среднего, являющийся мерой разброса вероятностного распределения:

для дискретной Х

для непрерывной Х

  для любой.

7. Среднеквадратичным отклонением случайной величины называется квадратный корень из дисперсии этой величины : .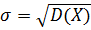

 

Функционирование элементов системы, подверженных случайным воздействиям, задается генераторами слу­чайных чисел, реализуемых программными методами, вырабатывающими псевдослучайные последовательности. Псевдослучайными последовательностями называют впол­не детерминированные числа, обладающие статистиче­скими свойствами случайных чисел, определяемых путем их проверки специальными тестами, а также периодич­ностью, т. е. повторяемостью через определенные проме­жутки времени. При моделировании используются интер­валы последовательностей псевдослучайных чисел, в ко­торых нет одного числа, встречающегося более одного раза.

Равномерно распределенные случайные числа в процессе генерации случайных величин с другими вероятностными распределениями, в том числе нормальным, пуассоновским и биномиальным. В настоящее время известно множество методов машинной имитации равномерно рас­пределенной случайной величины r(где 0£r£1). Соответствующие программы-генераторы вычисляют так называемые псевдослучай­ные числа, которые, хотя и определяются вполне детерминиро­ванными отношениями, обладают статистическими свойствами слу­чайных чисел, равномерно распределенных на интервале (0,1). Псевдослучайную последовательность, выдержавшую ряд специ­альных статистических тестов (частотных, автокорреляционных и т. д.), можно использовать как «истинно» случайную, хотя в дей­ствительности она таковой не является.

Прежде чем перейти к описанию конкретных генераторов псев­дослучайных чисел, сформулируем набор требований, которым обязан удовлетворять идеальный генератор. Полученные с его по­мощью последовательности должны состоять из:

(1) равномерно распределенных,

(2) статистически независимых,

(3) воспроизво­димых и

(4) неповторяющихся чисел.

Кроме того, генератор дол­жен (5) работать быстро и (6) занимать минимальный объем машин­ной памяти. Конгруэнтные процедуры, описанные здесь, удовлет­воряют всей совокупности перечисленных требований лучше, чем любые другие методы генерирования случайных чисел.

Мы рассмотрим 3 метода построения псевдослучайных последо­вательностей на ЭВМ — (1) мультипликативный, (2) смешанный и (3) комбинационный методы. После описания механизмов и некото­рых свойств этих процедур мы кратко остановимся на проблеме автокорреляции псевдослучайных чисел и различных тестах, с помощью которых оценивается их «случайность».

Методы генерирования псевдослучайных чисел. Конгруэнтные методы

 

Для любой конгруэнтной процедуры можно получить формулу, позволяющую найти i-й член определяемой ею последо­вательности псевдослучайных чисел {п₀, п₁, п₂,..., п _i , … }, не зная никаких членов, кроме нулевого. Тем не менее, в практических приложениях эту последовательность можно рассматривать как реализацию случайного процесса, если только она выдержит ряд специальных статистических тестов, состав которых определяется способом ее применения. Иногда, например, достаточно, чтобы псев­дослучайные числа были равномерно распределены и статистически независимы. (Можно показать, что конгруэнтные методы достаточ­но хорошо удовлетворяют этим условиям.) Все конгруэнтные гене­раторы автоматически удовлетворяют также требованиям (3) и (6), перечисленным выше, поскольку генерируемые с их помощью по­следовательности полностью воспроизводимы и занимают мини­мальный объем машинной памяти. Только степень выполнения (4) и (5) целиком определяется свойствами конкретной схемы. Поэтому рассматриваемые в дальнейшем процедуры анализируются именно с этих позиций.

В основе конгруэнтных процедур генерирования псевдослучай­ных чисел лежит математическое понятие сравнения.

Говорят, что два целых числа а и b сравнимы по модулю т, если их разность кратна числу т. Отношение сравнения записывают aºb(mod т) и читают: «а сравнимо с bпо модулю m». Это значит, что разность а — b делится на т без остатка, т. е. числа а и bдают одинаковые, остатки при делении на т. Например, 1897º7 (mod 5) и 4339º39 (mod 10²).

Все конгруэнтные методы опираются на рекуррентную формулу:

                               (1)

где п _i , т, l и m — неотрицательные целые числа. Запишем (1) при i=0, 1, 2...:

 

 

(2)

…

 

.

Если дано начальное значение n₀, множитель l  и аддитивная константа m, то (2) определяет последовательность целых чисел {n₁, n₂,…, n_i,…}, составленную из остатков от деления на m членов последовательности  Таким образом, для любого i≥1 справедливо неравенство . По целым числам после­довательности {n_i} можно построить последовательность {r_i}= = {n_i/m}рациональных чисел из единичного интервала.

Естественно возникает вопрос о существовании наименьшего положительного числа h, при котором n_h º n₀(mod m)(число hназывают периодом последовательности {n_i}). Если такое число b, существует, то как надо выбрать параметры n₀ , т, l и m  , чтобы сделать период максимальным? Величина hсущественна, поскольку n_h º n₀(mod m)влечет за собой n_h+1=n₁, n_h+2=n₂,.... Таким обра­зом, последовательность {n_i}будет периодической, т. е. значения ее членов будут повторяться через hномеров.

Можно показать, что период h всегда существует, причем его максимальное значение является монотонно возрастающей функцией модуля m. Это значит, что конгруэнтные методы не позволяют строить последовательности неповторяющихся псевдослучайных чисел. Тем не менее, в практических ситуациях можно обеспечить удовлетворительную величину периода h, выбирая достаточно боль­шой модуль или применяя другие способы.

 

Мультипликативный конгруэнтный алгоритмзадает последо­вательность неотрицательных целых чисел {n_i}, не превосходящих т, по формуле:

                    (3)

 

представляющей собой частный случай формулы (1) при m=0. Оказалось, что этот метод обладает достаточно хорошими статисти­ческими характеристиками. Выбирая соответствующим образом параметры l и п₀, с его помощью можно получить последователь­ности равномерно распределенных некоррелированных псевдослу­чайных чисел.

Более того, при выполнении определен­ных условий на эти параметры генерируемая мультипликативным алгоритмом последовательность обладает максимальным при дан­ном модуле периодом. Поскольку метод полностью детерминиро­ван, последовательности полностью воспроизводимы. Мультипли­кативный алгоритм требует минимального объема машинной памяти. С вычислительной точки зрения он сводится к последовательному подсчету произведения двух целых чисел — операции, которая очень быстро выполняется современными ЭВМ.

Для численной реализации наиболее удобна версия алгоритма, в которой модуль т равен p^e, где p — число цифр в системе счис­ления, используемой в машине, а е — длина машинного слова, отводимого под запись числа. Для двоичной машины p=2, для десятичной р=10. Величина е для ЭВМ с фиксированной длиной слова задана, а для ЭВМ с переменной длиной слова ее выбор оста­ется на усмотрение программиста. В дальнейшем вместо е мы будем употреблять символы bи d, относящиеся соответственно к двоич­ной и десятичной ЭВМ.

Выбор т= p ^е удобен по двум причинам.

1. Во-первых, вычисление остатка от деления на т сводится к выделению е младших разрядов делимого;

2. во-вторых, преобразование целого числа в рациональную дробь из интервала (0,1) осуществляется подстановкой слева от него двоичной или десятичной запятой.

Таким образом, специаль­ный выбор числа т позволяет исключить из процесса счета две опе­рации деления.

Так как в большинстве ЭВМ используются двоичная и десятич­ная системы счисления, мы рассмотрим мультипликативный метод именно в этих двух случаях. При этом нас будут интересовать только последовательности, порождаемые отношением сравнения вида

 

Двоичные машины

 

В этом случае m==2^b, где b — число двоичных цифр (битов) в машинном слове. Максимальный период последовательности, гене­рируемой мультипликативной процедурой, равен 2^b-2. Алгоритм построения последовательности с максимальным периодом таков:

1. Выбрать в качестве параметра n₀ произвольное нечетное чис­ло.

2. Вычислить коэффициент lпо формуле l=8t±3, где t — любое целое положительное число.

3. Вычислить произведение ln₀. Полученное число содержит не более 2 b значащих разрядов. Взять bмладших в качестве пер­вого члена последовательности, n₁остальные отбросить.

4. Вычислить дробь из интервала (0,1) по формуле r₁=n₁/2^b.

5. Вычислить очередное псевдослучайное число n₁ +1 как bправых разрядов произведения ln₁и вернуться к п. 4.

 

В качестве иллюстрации описанной схемы рассмотрим пример, в котором b=4. Мультипликативная процедура должна опреде­лить 4 разных числа (h=2^4-2=4).

1. Положим n₀=7. В двоичной форме записи n₀=0111.

2. При t=1 коэффициент l можно взять равным 11 или 5. Мы выберем l =5, или в двоичной форме, l = 0101.

3. ln₀= (0101)(0111) = 00100011. Отсюда n₁ = 0011  и r₁ = 3/16 = 0,1875.

4. ln₁= (0101)(0011) = 00001111. Отсюда n₂ = 1111  и r₂ = 15/16 = 0,9375.

5. ln₂= (0101)(1111) = 01001011. Отсюда n₃ = 1011  и r₃ = 11/16 = 0,6875.

6. ln₃= (0101)(1011) = 00110111. Отсюда n₄ = 0111 =n₀ и r₄ = 7/16 = 0,4375.

 

Для 32х разрядного машинного слова m=2³¹ = 2147483648. При этом в 32хразрядном машинном слове, максимальное целое число, размещающееся в машинном слове, равно 2³¹ -1, cледовательно m = 2147483647, b - простое число относительно m: b=2531011, l=8t±3, где t целое число, l = 214013.

Метод Неймана (метод квадратов)

В квадрат возводится, текущее случайное число и из результатов средних разрядов выделяется следующее случайное число, т.е. используется итерация:

· z₀ равно некоторому n- разрядному целому числу (например, 9876)

· z₁ определяется следующим образом : z₀*z₀ = 97535376 , z₁ =5353 z₂ =6546 и т.д.

r _i+1 = z _i+1 /10ⁿ

3. Метод произведений

Два следующих друг за другом случайных числа умножают и из произведения средних разрядов выделяют следующее случайное число.

 

Проверка генераторов равномерно распределенных псевдослучайных чисел

Выделяют три вида проверки: на периодичность, на случайность, на равномерность. При проверке на случайность используется совокупность тестов проверки: 1) частот, 2) пар, 3)комбинаций, 4) серий, 5) корреляции.

 

Тест проверки частот предполагает разбиение диапазо­на распределения на q интервалов и подсчет количества попаданий случайных чисел в выделенные интервалы. Возможно использование критериев согласия. Вероят­ность попаданий в заданный интервал теоретического распределения определяется по формуле

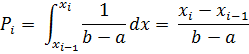
где x_i - верхний предел i-го интервала.

 

Тест проверки пар заключается в подсчете количества «1» для каждого разряда случайного числа. В этом слу­чае используется критерий согласия c² с одной степенью свободы. Теоретическая вероятность появления «1» для равномерно распределенных случайных чисел p_i =1/2. Поразрядный анализ позволяет отбросить неслучайные разряды, в качестве которых часто оказываются млад­шие разряды с преобладанием в них «1».

Тест проверки комбинаций сводится к подсчету коли­чества «1» в случайных числах. Можно использовать также критерии согласия. Теоретическая вероятность появления комбинации с i-м количеством «1» будет:  где k — количество разрядов случайного числа.

 

Тест проверки серий заключается в подсчете коли­чества различных длин последовательностей одинаковых значений случайных чисел. Возможно использование критериев согласия. Теоретическая вероятность , где 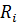 — количество серий i-и длины в N случайных числах; — общее количество серий в N случайных чис­лах при гипотетическом распределении.

Характерная особенность приведенных формул теста серий — независимый учет серий различной длины. На­пример, одна и та же серия, состоящая из четырех еди­ниц, учитывается как одна серия из четырех, две — из трех и три — из двух единиц.

Тест проверки корреляции заключается в определении коэффициента корреляции. При этом выполняют следующие действия:

· запускают два генератора случайных чисел на отрезке апериодичности с некоторой разницей между собой;

· подсчитывают коэффициент корреляции между этими последовательностями.

Проверка на равномерность. При про­верке на равномерность можно использовать тест про­верки частот, так как гистограмма частот хорошо отра­жает равномерность распределения случайных чисел по всему диапазону изменения. Для равномерного распре­деления случайных чисел  и .

Задаемся доверительной вероятностью w того, что оценка математического ожидания M^* не выйдет за пределы доверительного интервала:

Р{|М - M^*| < e} = w или Р{М - e < М^* < M + e}= w,

где M=(a+b)/2, - теоретические величины математического ожидания и среднеквадратичного отклонения, e - бесконечно малая величина. Величина w должна быть достаточно большой и составлять 0.9, 0.95, 0.99.

ЗАДАНИЕ 1

Для стандартного генератора случайных чисел выбранного Вами языка программирования получить три последовательности N случайных чисел (N={100, 1000, 10000}), для которых определить следующие характеристики: математическое ожидание М, дисперсию D и среднеквадратичное отклонение .

Выполнить проверку частотности и равномерности генератора.

Построить графики Функций Р(X) для оценки частотности генератора. Для получаемой выборки N чисел Р(X) – вероятность попадания генерируемой случайной величины в соответствующий интервал ее области определения.

Сравнить результаты с теоретическими.

Для оценки равномерности генератора случайных чисел выполнить расчет математического ожидания M_i для i последовательностей из 1000 случайных чисел (i=1,2,..., 10) и для i последовательностей случайных чисел переменной длины (длина i-ой последовательности задается как i*1000; i = 1, 2, ..., 10). Построить графики зависимости разности (М-М_i) от номера последовательности i, где М - теоретическое математическое ожидание равномерного распределения случайных чисел, М_i - расчетное математическое ожидание для i-й последовательности случайных чисел, полученных от генератора. По данным результатам определить Р{|М-М_i|<s} - вероятность того, что отклонения расчетного математического ожидания от теоретического не превышают величину теоретического среднеквадратичного отклонения.

ЗАДАНИЕ 2

Запрограммировать заданный вариант генератора случайных чисел и выполнить для него задание 1.

Порядок выполнения работы:

1. Изучить теоретическую часть, ответить на контрольные вопросы.

2. Получить у преподавателя свой вариант задания

3. Выполнить задания 1 и 2.

4. Оформить отчет.

Содержание отчета:

1. Описание и текст процедур заданий 1 и 2. Полученные результаты и графики.

2. Сравнение характеристик стандартного и запрограммированного генераторов случайных чисел.

3. Выводы.

Контрольные вопросы

1. Пусть стохастический процесс заключается в 3-х бросаниях монеты. Случайная величина X, характеризующая его, пусть обозначает число орлов, выпавших в результате 3-х бросаний. Построить для Х функции Р(х) и F(x).

2. Построить F(x) по заданной f(x).

3. Может ли быть случайная величина одновременно и дискретной и непрерывной?

4. Каков "физический" смысл понятий математическое ожидание и дисперсия?

5. Какие способы генерации случайных чисел Вы знаете?

6. Каким требованиям должны удовлетворять генераторы псевдослучайных чисел?

 

Варианты заданий

1. Метод серединных квадратов

2. Метод серединных произведений

3. Метод перемешивания

4. Линейный конгруэнтный метод

5. Инверсный конгруэнтный метод

Лабораторная работа № 2

---

Дата добавления: 2020-04-25; просмотров: 681; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!