Энтропия и энтальпия несжимаемой среды
В качестве независимых переменных будем считать давление и температуру Т, р.
Среда несжимаемая, следовательно,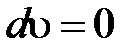 
, 
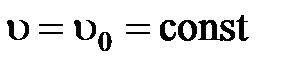
Воспользуемся объединенной математической записью первого и второго начал термодинамики
.
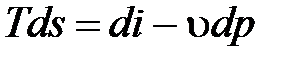Решим его относительно дифференциала энтропии:
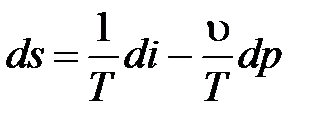(4.11)
Составим выражение для полного дифференциала энтальпии в системе с р, Т независимыми переменными
.
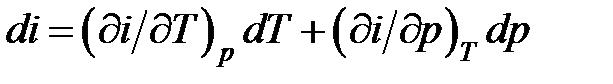После подстановки в выражение для дифференциала энтропии получим
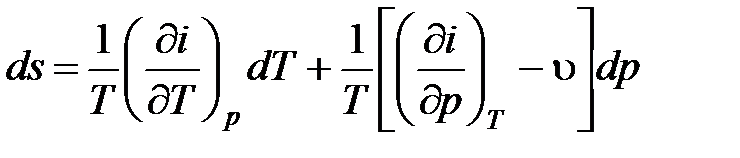. (4.12)
Откуда следует,
; 
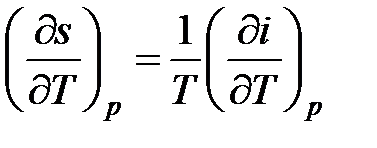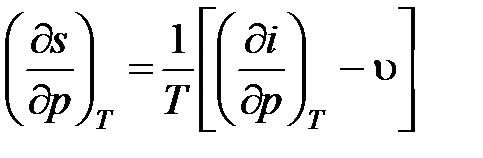. (4.13)
Из условия тождества вторых “смешанных” производных
.
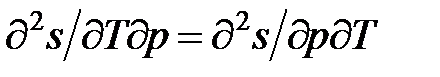Продифференцируем (4.13) первое выражение по давлению р, а второе по температуре Т и приравняем полученные результаты
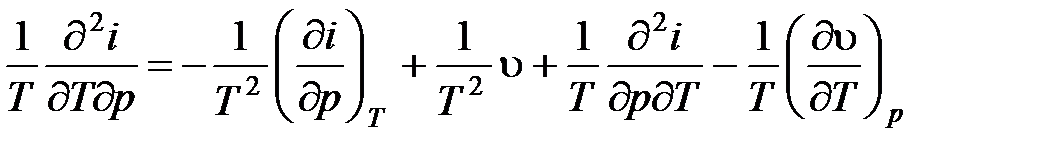. (4.14)
Приведем подобные члены, переписав и умножив на Т
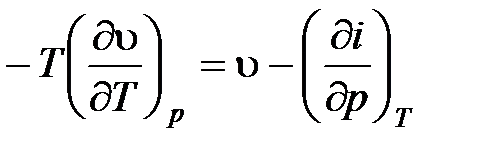. (4.15)
После очевидных алгебраических преобразований получим
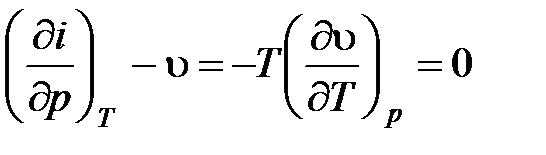. (4.16)
Для несжимаемой жидкости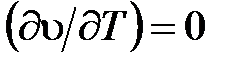 
,
тогда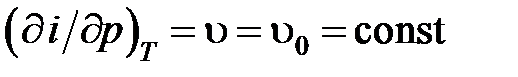 
.
Энтальпия несжимаемой среды линейно зависит от давления.
Т. к.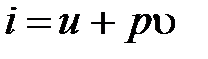 
, то
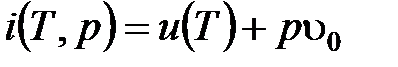. (4.17)
Внутренняя энергия несжимаемой среды зависит лишь от температуры. В результате получим
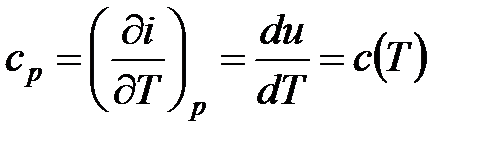. (4.18)
Для несжимаемой жидкости нет различий между изобарной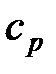 
и изохорной 
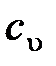теплоемкостями. Запишем выражения для внутренней энергии
|
|
|
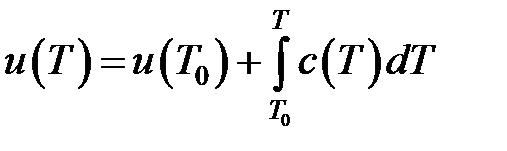. (4.19)
Энтальпия рассчитывается по известной внутренней энергии
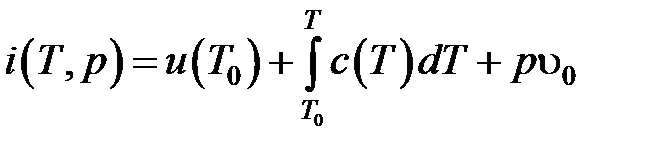. (4.20)
Энтропия несжимаемой среды зависит только от температуры. Покажем это
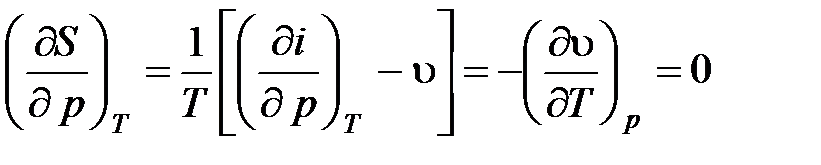. (4.21)
Интегрирование выражения (4.12)
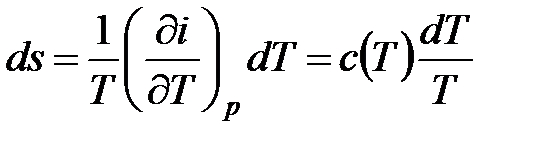
дает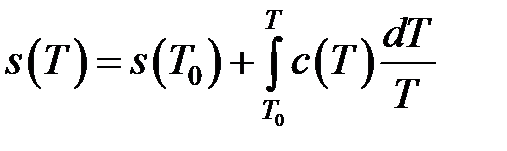 
. (4.22)
Если считать 
, то (4.22) можно переписать в виде
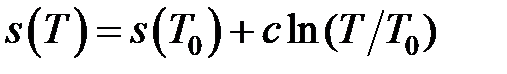. (4.23)
4.4 T, S – диаграмма
В соответствии со Вторым законом термодинамики изменение энтропии закрытой системы связано с теплом соотношением
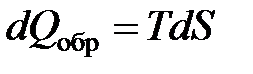
или для удельной энтропии
; 
.
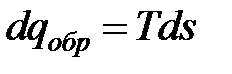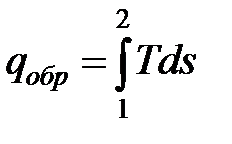Широкое распространение при анализе термодинамических циклов получила тепловая T, S – диаграмма.
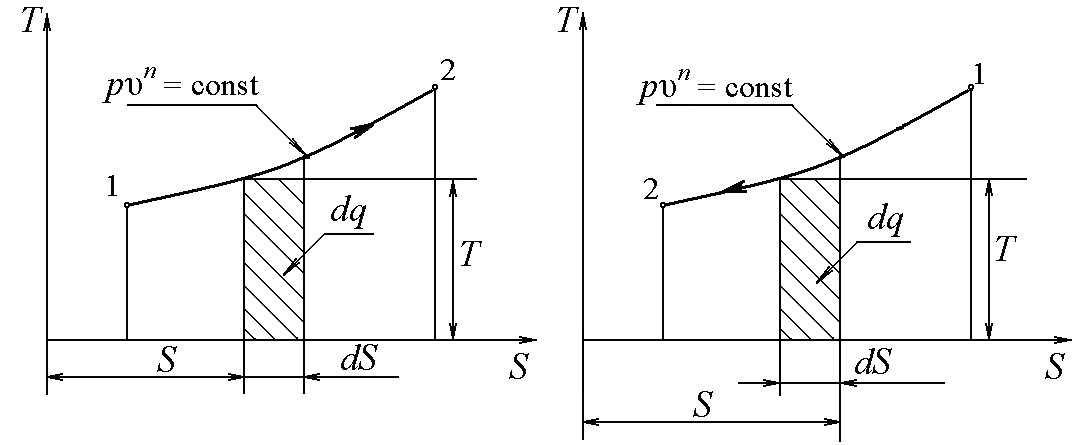
Тогда в T, S – диаграмме площадь под кривой процесса, спроектированная на ось энтропий, численно равна подведённой в нём теплоте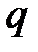 
(рисунок 4.2)
| а) dq > 0 б) dq < 0 Рисунок 4.2 Изображение процессов в T, S – диаграмме |
Действительно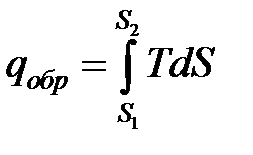 
.
В частности для изотермического процесса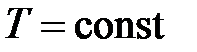 
получим
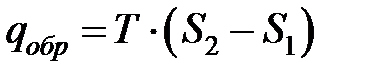
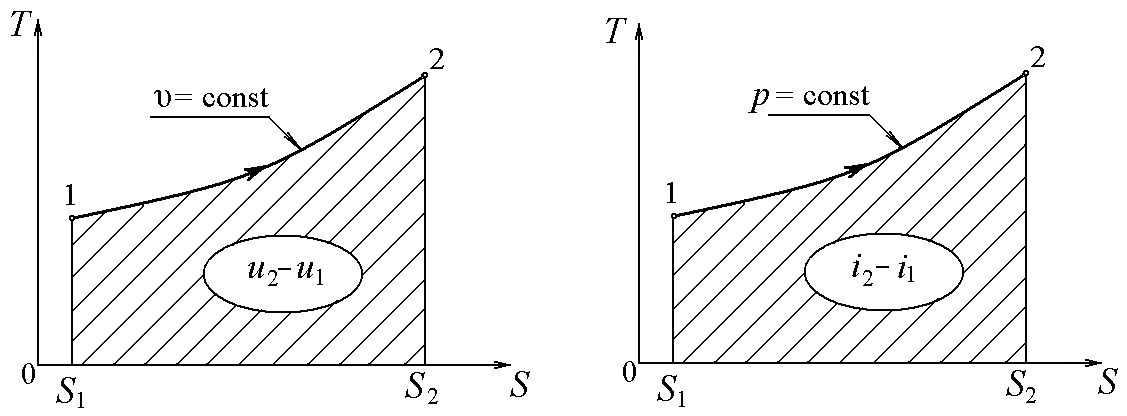
| а) б) Рисунок 4.3 Изохорный (а) и изобарный (б) процессы в T, S – диаграмме
|
Для изохорного
; 
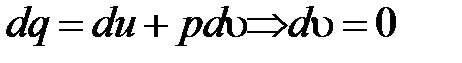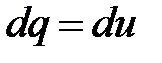
и изобарного процессов
; 
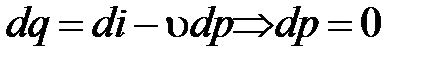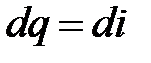
площади под кривой процесса представляют собой внутреннюю энергию и энтальпию.
Дата добавления: 2020-04-25; просмотров: 156; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!