Лекция 2 ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
Задания и методические указания для самостоятельной работы студентов
Для успешного усвоения учебного курса и выполнения домашнего задания студенту необходимо самостоятельно выполнить следующие этапы:
1. Проработка лекций, самостоятельная работа с учебной литературой по теме лекции, используя онлайн-ресурсы Образовательный портал НИЯУ МИФИ online.mephi.ru и НПОО https://openedu.ru
2. Подготовить конспект лекций
3. Решить следующие задачи:
Задание №1: Иродов И.Е. Задачи по общей физике , 2004 г.
Номера задач: 2.32, 2.33, 2.47, 2.55
Задание №2: Иродов И.Е. Задачи по общей физике , 2004 г.
Номера задач: 2.141, 2.140, 2.146, 2.144 Базаров И.П. Термодинамика, Номера задач:3.26,3.27,3.30
4. Прислать скан или фото решенных задач и конспектов (в разборчивом виде) Катаевой Галине Валентиновне на электронную почту: galvk@mail.ru с пометкой «МФ-21»
Срок выполнения домашнего задания №1: 06.04.2020 г.
Срок выполнения домашнего задания №2: 13.04.2020 г.
ЛЕКЦИИ ПО ТЕРМОДИНАМИКЕ
Лекция 1 Термическое уравнение состояния газовой смеси
Запишем уравнение состояния для i-го компонента газовой смеси, если он занимает весь ее объем и находится там при температуре смеси. Тогда его давление равно парциальному:
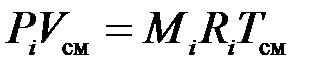. (3.14)
Просуммируем полученные зависимости для всех компонентов, входящих в смесь
.
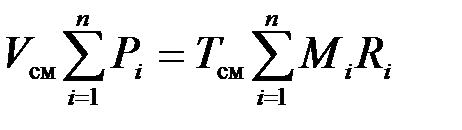Вспоминая, что 
и, вводя обозначение 
,
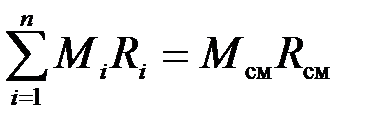получим уравнение состояния газовой смеси:
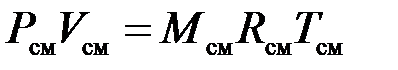, (3.15)
где Rсм – газовая постоянная смеси. Ее величина может быть рассчитана из соотношения
.
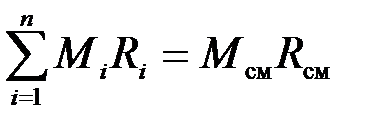Поделив его на массу смеси М, получим соотношение:
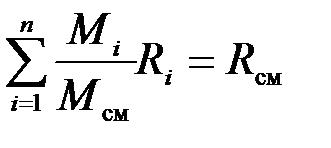, но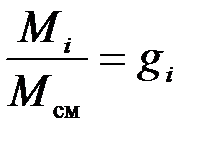 
,
тогда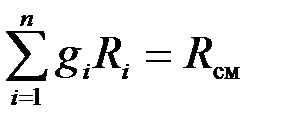 
. (3.16)
Введение понятия о кажущейся молекулярной массе смеси упрощает расчеты газовых смесей:
. (3.17)
Или после подстановки выражения (3.17) для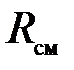 
получим с учетом равенства 
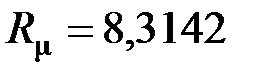Дж/(моль∙К)
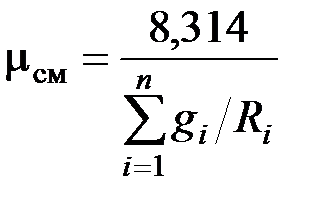. (3.18)
Запишем уравнение состояния для массы газа mi:
или, с учетом 
;
.
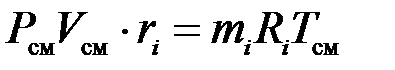Последнее выражение преобразуем к виду
.
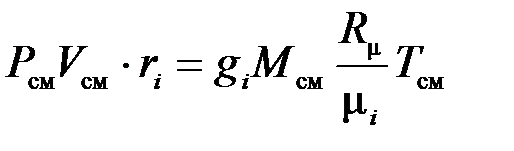Если записать выражения для каждого компонента смеси, а затем просуммировать, получим
; 
,
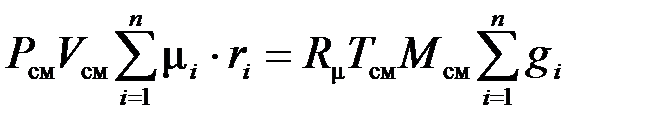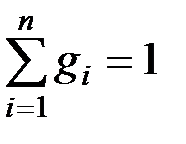тогда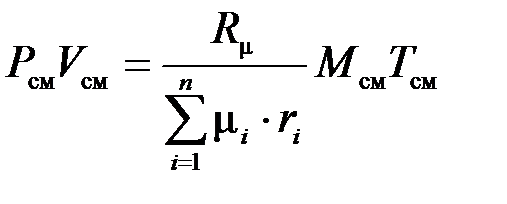 
.
Таким образом 
, а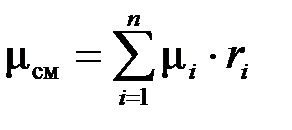 
. (3.19)
Получим расчетные зависимости для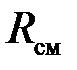 
и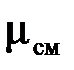 
, если смесь задана массовыми долями 
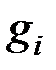. Запишем уравнение состояния для М кг газовой смеси и для 
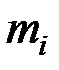кг компонентов газов, входящих в смесь, через их парциальные объемы:
; 
.
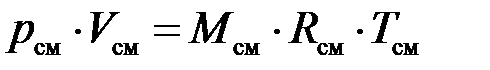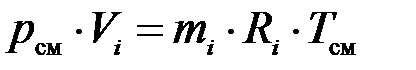Если записать второе выражение для каждого компонента, а затем их просуммировать, то получим
.
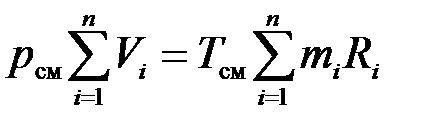Перепишем его в виде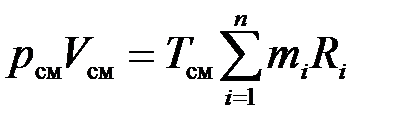 
.
Поделив последнюю зависимость на уравнение состояния смеси для М кг, получим зависимость для расчета Rсм и mсм через массовый состав:
; 
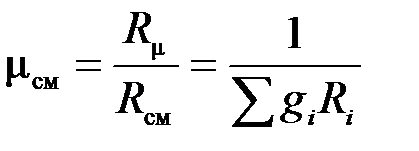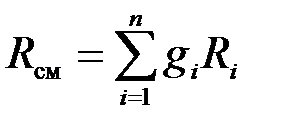. (3.20)
Последние выражения позволяют по объемным долям и молекулярным массам компонентов рассчитать газовую постоянную смеси и среднюю молекулярную массу.
Зная соотношения между массовыми и объемными долями газов, можно рассчитать парциальные давления
; 
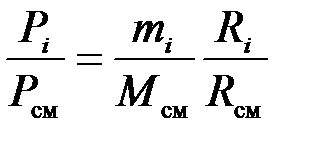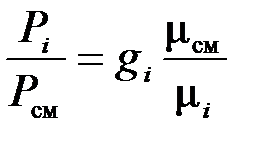или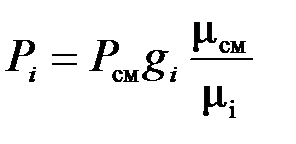 
. (3.21)
Запишем закон Бойля-Мариотта для i-го компонента и всей смеси
,
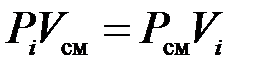откуда 
,
тогда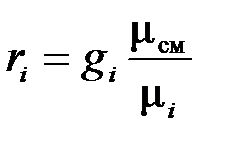 
или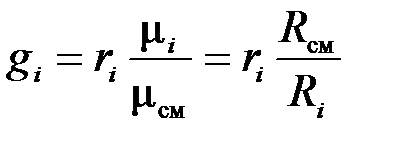 
. (3.22)
Приравнивая зависимости (3.21) и (3.22), получим формулы перевода массовых долей в объемные и наоборот:
; 
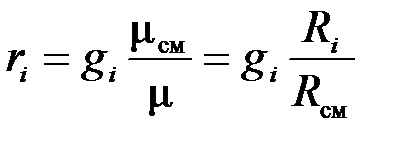. (3.23)
Плотность газовой смеси:
,
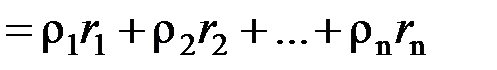таким образом, 
. (3.24)
Выразим 
через массовый состав смеси:
,
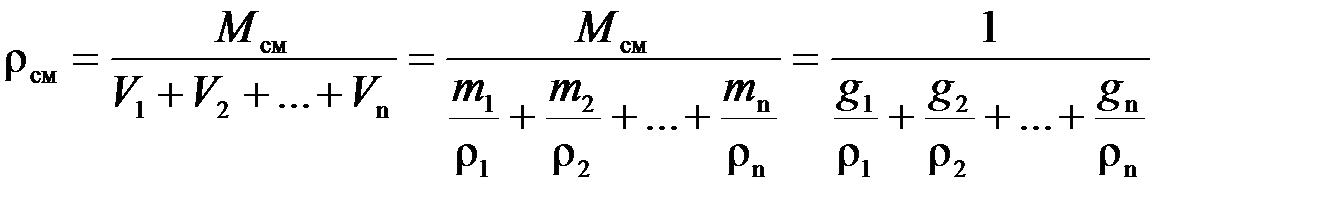следовательно, 
.
Теплоемкость смеси газов
Пусть известны ci – зависимость массовых теплоемкостей компонентов от температуры
.
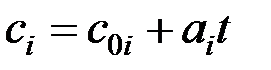Для одного килограмма газовой смеси массовая теплоемкость может быть рассчитана по формуле
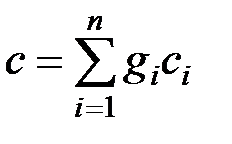. (3.25)
Или с учетом зависимости теплоемкостей от температуры
.
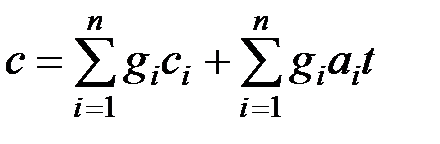Если задан объемный состав, то удобней пользоваться объемными теплоемкостями:
для 1 м3 компоненты: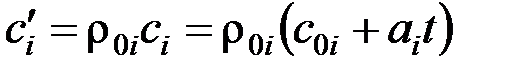 
,
для 1 м3 смеси: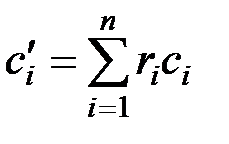 
. (1.26)
Или с учетом зависимости от температуры:
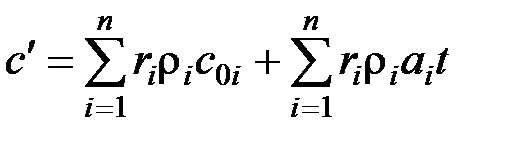. (1.27)
Энтропия газовой смеси
Воспользовавшись объединенным выражением первого и второго начал термодинамики, запишем
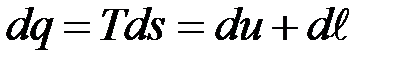
или
.
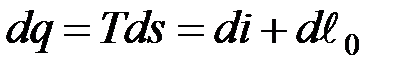Распишем выражения, входящие в правые части
; 
; 
; 
.
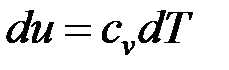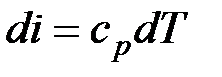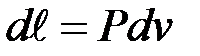Тогда после подстановки получим
; 
.
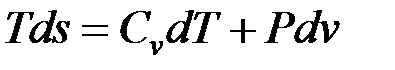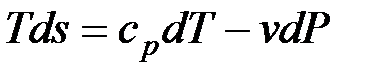Предполагая газ совершенным, а, следовательно, подчиняющимся уравнению состояния в форме Клапейрона-Менделеева, преобразуем, правые части к виду удобному для интегрирования (исключим лишнюю переменную)
; 
.
Запишем уравнение состояния и выразим из него давление и удельный объем
; 
; 
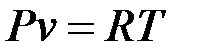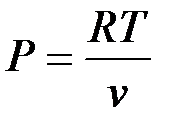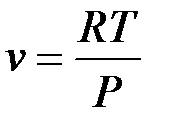или 
; 
.
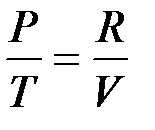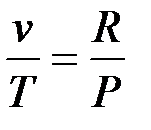После подстановки в (3.26) и (3.27)
; 
.
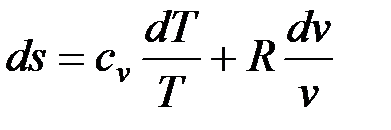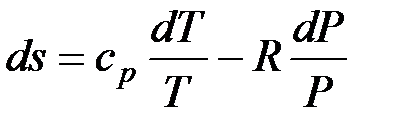Проинтегрируем (3.26) и (3.27) от состояния 1 до состояния 2:
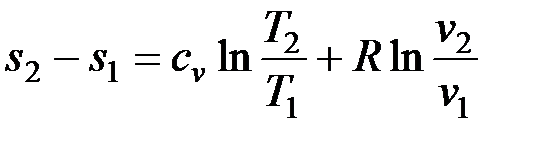; (3.28)
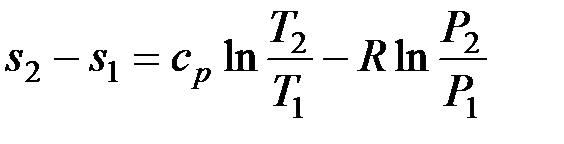. (3.29)
Если в качестве независимых переменных будут выбраны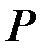 
и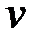 
, то выражение для расчета изменения энтропии в политропных процессах может быть преобразовано к виду
. (3.30)
Известно, что энтропия является аддитивной функцией состояния, а, следовательно, для системы, состоящей из «n» частей, должны вычисляться соотношения
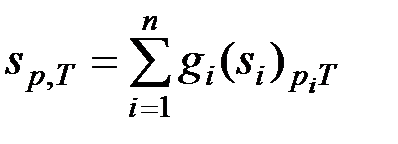. (3.31)
С другой стороны энтропия может быть рассчитана по зависимости, в которой в явной форме аддитивность не отражена
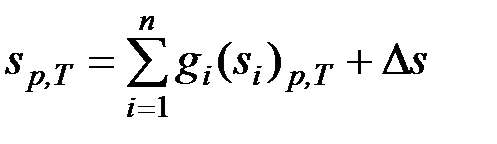. (3.32)
По своей сути выражения (3.32) и (3.31) эквивалентны.
Энтропия смеси идеальных газов представляет собой сумму энтропий газов, входящих в смесь
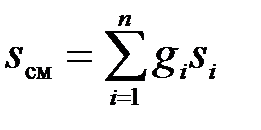. (3.33)
Для газа с параметрам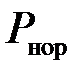и 
и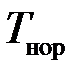 
следует, что его энтропия в соответствии с (1.29) равна
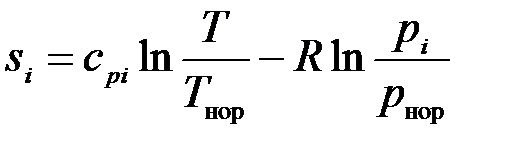, (3.34)
где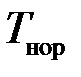 
– температура нормировки; 
– парциальное давление;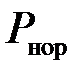 
– давление нормировки.
Парциальное давление компонента в смеси можно определить по ранее приведенной зависимости
.
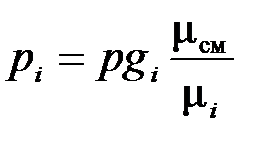Тогда второе слагаемое правой части выражения (3.34) может быть сведено к виду
.
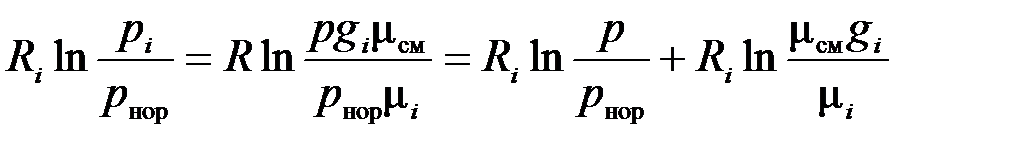Следовательно, выражение для энтропии газовой смеси (3.33), представленное в виде аналогичном (1.31), можно переписать
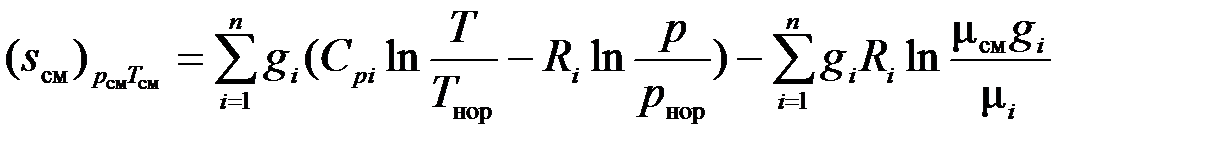. (3.35)
Выражение, стоящее в скобках в правой части (3.35), представляет собой энтропию 1 кг компонента при параметрах смеси, которую можно обозначить, как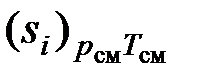 
, а последнюю сумму можно определить как приращение энтропии в процессе необратимого смешения идеальных газов, входящих в смесь. Так как по смыслу величина 
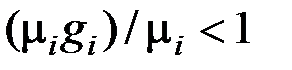, то выражение (1.35) может быть переписано в виде
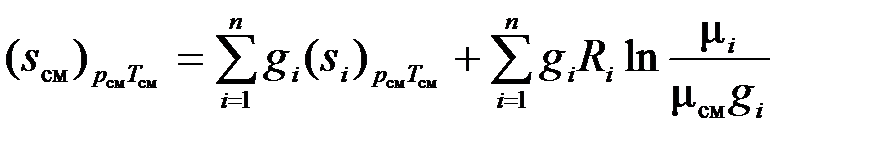. (3.36)
Учитывая формулу соотношения массовых и объемных долей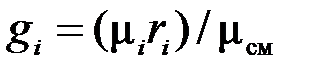 
, перепишем (3.36)
. (3.37)
Из (3.37) следует, что смешение различных газов при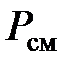 
, 
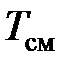приводит к возрастанию энтропии на величину энтропии смешения
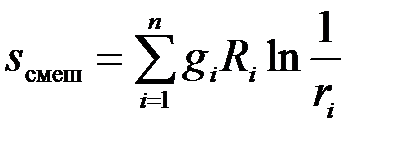(3.38)
или для отдельно взятого i-го компонента
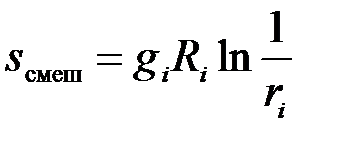. (3.39)
Выражение (3.32) учитывает возрастание энтропии i-го компонента за счет необратимости процесса смешения.
Лекция 2 ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
Основные принципы Второго закона термодинамики, сформулированные в курсе общей физики, отражают связь энтропии со статистическим весом и вероятностью состояния. Показано, что отношение бесконечно малого количества теплоты к абсолютной температуре приводит к появлению нового параметра состояния 
– энтропии, дифференциал которой для термодинамических процессов подчиняется неравенству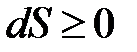 
, где 
лишь для обратимых процессов (циклов), а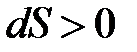 
для необратимых. Очевидно, что если энтропия S является параметром состояния, то для обратимых процессов должно выполнятся условие 
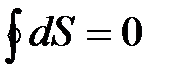. Для произвольных циклов как обратимых, так и необратимых
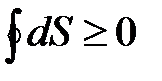. (4.1)
Дата добавления: 2020-04-25; просмотров: 95; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!