Траектория снаряда без учета сопротивления воздуха.
Министерство образования и науки российской федерации
Чайковский филиал
федерального государственного бюджетного
образовательного учреждения высшего профессионального образования
«Пермский национальный исследовательский политехнический университет» (ЧФ ПНИПУ)
Кафедра автоматизации, информационных и инженерных технологий
Механика
Лабораторная работа №2
““Задача внешней баллистики”
Выполнил: студент АТПП-19-бозЧФ
Очно-заочного отделения
Деревнин А.Ю.
Проверил: профессор доктор технических наук
Морозов Е.А.
2019
Содержание
Введение…………………………………………………………………………………...3
Траектория снаряда без учета сопротивления………….…………………………. 5
Траектория снаряда с учетом сопротивления воздуха ……………...…………...11
Траектория снаряда в изотермической атмосфере…….…………………..….….13
Введение.
Баллистика - военно-техническая наука, основывающаяся на комплексе физико-математических дисциплин, рассматривающая движение артиллерийских снарядов, пуль, мин и т. п. Процессы, протекающие внутри канала ствола при выстреле, изучает внутренняя баллистика. Внешняя баллистика занимается процессами, которые протекают от момента вылета снаряда из канала ствола до момента ее встречи с целью. Внешняя баллистика основывается на законах механики, тесно связана с аэродинамикой, гравиметрией и теорией фигуры Земли. Баллистический расчет дает все основные данные о траектории и характеристиках движения снаряда, исходя из которых можно судить о необходимых для оружия параметрах.
|
|
|
Настоящая дидактическая разработка посвящена баллистике - науке о движении тяжѐлых тел, брошенных в пространстве, основанная на математике и физике, а также вычислительной технике.
Цель построить достаточно полную теорию баллистики - движения снарядов в реальной среде с учетом сопротивления и размеров (геометрии) тела.
Актуальность выполняемой работы обусловлена решением обратной задачи баллистики – результатами экспериментальных данных траекторий полетов и фактических данных о размерах снарядов оценка характеристик и параметров сопротивления.
Задачи:
· Создать компьютерную модель траектории снаряда без учета сопротивления воздуха.
· Создать компьютерную модель движения снаряда в атмосфере с постоянной плотностью
· Создать компьютерную модель движения снаряда в атмосфере, плотность которой убывает по закону экспоненты.
|
|
|
Постановка классической задачи.
Рассмотрим кинематику движения тела (материальной точки) в однородном гравитационном поле Земли на примере рис. 1.
Тело бросается начальной скоростью v 0 под углом α к горизонту. Так как на тело действует только одна сила тяжести mg, то будет иметь место плоское движение. Через векторы g и v0 построим плоскость, в которую установим декартовую прямоугольную систему координат x0y, точку, из которой производится выстрел. Кинематика движения тела, брошенного под углом к горизонту.началом координат. Ось 0x направим по горизонту в сторону выстрела, а ось 0y - вертикально верх. - 5 - Очевидно, что движение в горизонтальном направлении равномерное с постоянной скоростью v 0cosα, тогда как движение в вертикальном направлении – равноускоренное с начальной скоростью v 0sinα и постоянным ускорением –g. Вводя переменную времени t, напишем соответствующие уравнения движения: x = v0tcosα(1.1а) и y = v0tsinα –gt2 /2(1.1б), а также соотношения для скоростей: vx = v0cosα = const и vy = v0sinα –gt.
Движение вверх продолжается до тех пор, пока вертикальное составляющее vy не приравняется нулю. Обозначив время подъема буквой τ вычислим его из уравнения:vy = 0:
|
|
|
Заметим, что это время из-за симметрии движения равняется времени спуска. Для получения уравнения траектории y = y(x), из уравнения (1.1а) вычислим время 
и поставим в уравнение (1.1б): 
, так что траектория представляет собой параболу. Вычислим высоту полета h 
, а также дальность полета: 
. Изложение параграфа завершим традиционным вычислением максимальной дальности, если стрельба производится постоянной скоростью v0 под всевозможными углами. Имея в виду, что тригонометрическая функция синус в выражении (1.6) принимает свое максимальное значение 1 при аргументе 2α = 900 , получим:
при 
=450.
Теоретическая часть.
Траектория снаряда без учета сопротивления воздуха.
Рассмотрим задачу о полете снаряда, вылетающего из орудия с начальной
скоростью 
под углом 
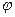к горизонту, который называется углом бросания. В первом приближение силу сопротивления воздуха не будем принимать во внимания.
Примем точку вылета снаряда из ствола за начало координат, ось 
направим горизонтально, ось 
– вертикально вверх. Тогда начальную скорость снаряда можно записать в её проекциях на оси
. (1)
|
|
|
По второму закону Ньютона ускорение снаряда
, (2)
где 
– равнодействующая сил действующих на снаряд,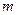 
– масса снаряда. В проекциях на оси координат закон (1) запишется в форме системы уравнений
. (3)
Так как мы рассматриваем простейший случай, при котором в процессе полета на снаряд действует только сила тяжести, направленная к земле, то 
, 
, и система уравнений (2) примет вид
. (4)
Из первого уравнения следует, что вдоль оси 
снаряд движется с постоянной скоростью, определяемой начальным условием (1), поэтому
. (5)
Второе уравнение (4) даёт
, (6)
откуда, интегрируя от 
до 
, находим 
или
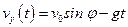. (7)
Для определения перемещений вдоль координатных осей запишем составляющие скорости в виде дифференциальных уравнений
. (8)
Пользуясь формулами (5) и (7) получаем из (8)
. (9)
В начальный момент времени снаряд был в начале координат, поэтому
. (10)
Интегрируя уравнения (9) от до 
и пользуясь начальными условиями(10), находим
. (11)
Формулы (11) определяют закон движения снаряда и дают возможность определить его положение в любой момент времени.
Беря различные значения , мы можем найти по формулам (11) положение снаряда в различные моменты времени и построить траекторию полета снаряда. Для этого можно воспользоваться программой построения графика параметрической функции.
Рис.2. Траектория движения снаряда.
На рисунке представлена траектория движения снаряда для случая 
, 
.
Из уравнений (11) нетрудно исключить и получить уравнение траектории в виде зависимости 
. Действительно, первое уравнение (11) даёт 
, после этого из второго уравнения (11) находим
, (12)
видим, что 
есть многочлен второй степени от 
, график такого многочлена – парабола.
Из (12) видно, что при одном и том же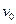 
форма траектории зависит от угла бросания 
. Найдём наибольшую высоту подъёма снаряда и дальность стрельбы при данных и 
. Для определения наибольшей высоты подъёма составим уравнение 
,
откуда
. (13)
При этом значении высота имеет максимум (физически ясно, что это максимум; впрочем, этот факт легко проверить по второй производной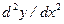 
). Подставляя найденное значение 
в (12), получим
. (14)
для определения дальности полёта достаточно определить то значение , при котором 
. (15) что отбрасывая не интересующее нас решение 
, находим
. (16)
Таким образом, дальность стрельбы зависит от начальной скорости и от угла бросания.
При каком же угле бросания при фиксированной начальной скорости, дальность стрельбы наибольшая. Ясно, что это будет, тогда, когда 
, т.е. при значении угла бросания .
Определим время, в течение которого снаряд поднимается вверх. Для этого достаточно решить уравнение 
, потому что в тот момент , когда достигает своего наибольшего значения, снаряд перестаёт подниматься и начинает падать. Условие даёт 
, откуда
. (17)
Полное время полета снаряда 
определим, исходя из того, что полет прекращается в тот момент, когда 
. Пользуясь первым уравнением (11) и (16), находим:
,
откуда
. (18)
Сравнивая (17) и (18), видим, что полное полетное время 
в 2 раза больше времени подъёма. Время подъёма снаряда равно времени его падения.
Отметим в заключении, что реальные траектории снарядов не являются в точности параболами, они несколько искажены, так как снаряд испытывает сопротивление воздуха. При этом дальность стрельбы, высота подъёма, полное время и т.п. зависят от массы снаряда, его формы и плотности воздуха. Это побуждает нас перейти к численному решению задачи внешней баллистики.
Для построения компьютерной модели движения снаряда, прежде всего, перепишем дифференциальные уравнения движения снаряда (5), (6), (8) вместе с начальными условиями
. (19)
Система (19), при заданных значениях 
, является динамической моделью движения снаряда при отсутствии силы сопротивления воздуха.
Для построения численного алгоритма интегрирования уравнений необходимо перейти от дифференциальных уравнений к разностным уравнениям. В качестве примера такого построения рассмотрим уравнение
. (20)
По определению производной
. (21)
Если 
считать малой, но не бесконечно малой величиной, то можно записать приближенное отношение
. (22)
Отношение (22) будет тем точнее, чем меньше мы берём интервал времени . Если выбрать интервал настолько малым, что погрешностью отношения можно пренебречь, то уравнение (20) можно заменить уравнением
. (23)
Запишем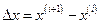 
, т.е. следующее значение 
минус предыдущее значение 
. Обозначим 
, и назовем его шагом численного интегрирования. Значение скорости 
будем брать при значении координаты , и в знак того будем писать 
. После этого уравнение (23) примет вид
. (24)
Выразим из (24) значение новой координаты 
. (25)
Поступая подобным образом, преобразуем систему дифференциальных уравнений (19) в систему разностных уравнений
. (26)
Подчеркнем, что при вычислении новых координат , 
используются значения скорости 
, 
вычисленные в первых двух уравнениях. Эта особенность делает процесс вычисления устойчивым к накоплению погрешности счета. Начальные условия, теперь можно записать в виде
. (27)
Система (26), вместе с начальными условиями (26) представляет собой алгоритм численного интегрирования динамической системы (19).
Для реализации компьютерной модели, возьмем за основу программу построения графика параметрической функции.
Введём обозначения для переменных:
– время и шаг интегрирования;
– координаты снаряда;
– проекции скорости снаряда;
– начальная скорость снаряда;
– угол бросания;
– ускорение свободного падения;
и объявим их действительный тип в начале программы.
Используя (26), (27) и введенные обозначения вместо блока построения графика параметрической функции, теперь запишем блок численного интегрирования:
// движение тела брошенного под углом к горизонту, численное решение
t:=0 {c} {время};
tt:=0.001 {c} {шаг интегрирования};
V0:=662{м/c} {начальная скорость снаряда};
f:=55 {градусы};
f:=f*Pi/180 {перевод градусов в радианы};
VX:=V0*cos(f); VY:=V0*sin(f) {составляющие начальной скорости};
X:=0 {м}; Y:=0 {м} {начальные координаты снаряда};
g:=9.8 {м/с c} {ускорение свободного падения};
For i:=1 to 100000 do
Begin
if Y<0 then Goto 5;
VX:=VX;
VY:=VY-g*tt;
X:=X+VX*tt;
Y:=Y+VY*tt;
SetPixel(X0+round(X*40*MasX),Y0-round(Y*40*MasY), clPurple);
5:t:=t+tt;
end;
На рис.3 приведен пример компьютерного расчета траекторий снаряда при различных углах бросания.
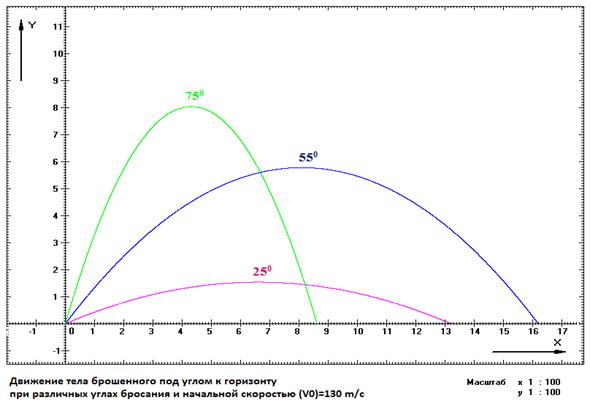
Рис. 3. Траектории тела брошенного под углом к горизонту
Сравнивая рисунки 2 и 3, мы видим совпадение аналитического и численного решения для угла бросания 
, что доказывает правильность работы программы.
Дата добавления: 2020-01-07; просмотров: 1782; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!