Зниження порядку диференціальних другого порядку
Основним методом інтегрування (знаходження загального розвязку або загального інтеграла) диференціальних рівнянь вищого порядку є зниження їх порядку і зведення до інтегрування диференціальних рівнянь першого порятку. Розглянемо деякі можливі видатки зниження порядку диференціальних рівнянь другого порядку.
1. Диференціальне рівняння не містить невідомої функції у, тобто має вигляд:
 (7).
(7).
У цьому випадку робимо заміну 
 і отримуємо диференціальне рівняння першого порядку стосовно невідомої функції Z:
і отримуємо диференціальне рівняння першого порядку стосовно невідомої функції Z:

Якщо знайдемо загальний розв’язок  , рівнянь (8) то далі інтегруємо рівняння
, рівнянь (8) то далі інтегруємо рівняння 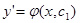 ; якщо ж знайдемо загальний інтеграл
; якщо ж знайдемо загальний інтеграл  то для знаходження розв’язків диференціального рівняння (7) отримуємо наявне диференціальних рівнянь першого порятку
то для знаходження розв’язків диференціального рівняння (7) отримуємо наявне диференціальних рівнянь першого порятку 
2. Диференціальне рівняння не містить явно аргументах х, тобто має вигляд
 (9)
(9)
У розв’язаному випадку приймаємо за невідому функцію  а й аргументи вважаємо у. Тоді маємо:
а й аргументи вважаємо у. Тоді маємо:

Підставимо вирази для у’,y” у рівняння (9), отримаємо відносно функцію  диференціальних рівнянь першого порядку:
диференціальних рівнянь першого порядку:
 (10)
(10)
Якщо знайдемо загальний розв’язок  рівняння (10), то дані інтнгруєм явне диференціальне рівняння першого порядку
рівняння (10), то дані інтнгруєм явне диференціальне рівняння першого порядку  яке є з розв’язком функції змінними; якщо ж знайдено загальний інтеграл
яке є з розв’язком функції змінними; якщо ж знайдено загальний інтеграл  рівняння (17.10), то дані інтегруємо наявне диференційне рівняння
рівняння (17.10), то дані інтегруємо наявне диференційне рівняння  першого порядку.
першого порядку.
|
|
|
Диференціальне рівняння (3) є однорідним відносно функції у та її похідних  і
і 
тобто

У цьому випадку виконуємо заміну  де z = z (x). Знаходимо
де z = z (x). Знаходимо  Підготовимо вирази для
Підготовимо вирази для  та
та  у рівняння (3) і використовуємо його однорідність:
у рівняння (3) і використовуємо його однорідність:

У результаті приходимо до диференціальних рівнянь першого порятку стосовно функції
 (11)
(11)
яке з точністюдо розвязку  рівносильне рівняню (3)
рівносильне рівняню (3)
Якщо знайдемо загальний розвязок  рівняння (11), то речі інтегруємо розв’язане дифененційне рівняння першого порядку
рівняння (11), то речі інтегруємо розв’язане дифененційне рівняння першого порядку  , яке є з відокремлюваними змінними; якщо ж знайдемо загальний інтеграл
, яке є з відокремлюваними змінними; якщо ж знайдемо загальний інтеграл  то приходимо до інтегрування наявного диференціального рівняння першого порядку:
то приходимо до інтегрування наявного диференціального рівняння першого порядку:

При зниженні порядку вихідного рівняння міг бути втрачений його розв’язок у=0. Але він не втрачений, отримуємо із загального розв’язку при 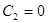
Лінійні диференціальні рівняння другого порядку
Диференціальні рівняння розв’язку порядку (3) називається лінійним, якщо функція,  є лінійно відносно
є лінійно відносно  тобто якщо воно має вигляд
тобто якщо воно має вигляд
 (12)
(12)
Будемо вважати, що розв’язком 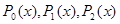 і вільний член q(x) x є(a,b) i
і вільний член q(x) x є(a,b) i  .
.
Якщо  то маємо відповідне лінійне однорідне рівняння
то маємо відповідне лінійне однорідне рівняння
|
|
|
 (13)
(13)
Якщо  ,то рівняння (12) називають лінійним не однорідним диференціальним рівняння другого порядку.
,то рівняння (12) називають лінійним не однорідним диференціальним рівняння другого порядку.
Питання для перевірки
1. Що називається диференціальним рівнянням вищого порядку ?
2. Задача Коші.
3. Основні методи інтегрування.
4. Лінійні диференціальні рівняння другого порядку.
Тестові завдання
1. Диференційні рівняння вищого порядку стосовно функції у(х) має вигляд:
1. 
2. 
3. 
2.Функція (вписати відповідь) де  і
і  довільні сталі називається загальним розв’язком диференційованого рівняння другого порядку, якщо вона є розв’язком цього рівняння для розв’язком функції
довільні сталі називається загальним розв’язком диференційованого рівняння другого порядку, якщо вона є розв’язком цього рівняння для розв’язком функції  і
і  і з якої за рахунок вибору значень цих сталих можна отримати будь-який розв’язок цього рівняння (за винятком може окремих).
і з якої за рахунок вибору значень цих сталих можна отримати будь-який розв’язок цього рівняння (за винятком може окремих).
3. Співвідношення  яким певно додається загальний розв’язок диференціального рівняння 2-го порядку, називається (вписати відповідь) цього рівняння.
яким певно додається загальний розв’язок диференціального рівняння 2-го порядку, називається (вписати відповідь) цього рівняння.
4. Диференціальне рівняння не містить невідомої функції у, тобто має вигляд:
1. 
2. 
3. 
5.Розв’язок який отримуємо із загального диференціального рівняння 2-го порядку, падаючи  і
і 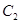 певних числових значень, називається числовим (вписати відповідь) цього рівняння.
певних числових значень, називається числовим (вписати відповідь) цього рівняння.
|
|
|
6. Графік функції  називається при цьому(вписати відповідь)диференціального рівняння (3) чи (4).
називається при цьому(вписати відповідь)диференціального рівняння (3) чи (4).
7. Диференціальні рівняння розв’язку порядку (3) називається лінійним, якщо функція,  є лінійно відносно
є лінійно відносно  тобто якщо воно має вигляд
тобто якщо воно має вигляд
1. 
2. 
3. 
8. Співвідношення … яким певно додається загальний розв’язок диференціального рівняння 2-го порядку, називається загальним інтегралом цього рівняння:
1. 
2. 
3. 
9. З теореми існування та розв’язку задачі Коші для рівняння (4) випливає, що при виконанні умов теореми в деякому околі точки 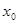 існує загальний розв’язок
існує загальний розв’язок  цього рівняння, з розв’язком якого отримати розв’язок задачі Коші, визначивши значення сталих
цього рівняння, з розв’язком якого отримати розв’язок задачі Коші, визначивши значення сталих  і
і 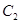 із системи рівнянь:
із системи рівнянь:
1. 
2. 
3. 
Задачі
Задача 1. Знайти розв’язок диференційoваного рівняння  що задовольняє умови
що задовольняє умови 

Розв’язання. Загальний розв’язок цього рівняння легко знайти шляхом інтегрування заданої рівності, бо тоді розв’язком функції  , друга похідна яких дорівнює 6х:
, друга похідна яких дорівнює 6х:

загальний розв’язок рівняння.
Задача 2. Знайти розв’язок рівняння  , який звдовольняє умови:
, який звдовольняє умови: 
 .
.
Розв’язання. Оскільки у рівнянні явно не входить аргумент х, то знижуємо його порядок підстановкою  з якої випливає, що
з якої випливає, що
|
|
|
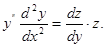
Підставити вирази для  і
і  , у дане рівняння, отримаємо диференціальне рівняння першого порядку
, у дане рівняння, отримаємо диференціальне рівняння першого порядку

яке рівносильне сукупності рівнянь:
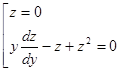
Інтегруємо друге рівняння, яке є з відокремлюваними змінними:


 .
.
При відокремлені зміних втраченими могли бути розвязки  і
і  . Ці розв’язки не є втраченими, бо перший з них співпадає з першим рівнянням сукупності, а другий отримуємо з сімї
. Ці розв’язки не є втраченими, бо перший з них співпадає з першим рівнянням сукупності, а другий отримуємо з сімї
 при
при 
Отже, множина всіх розв’язкв дискретного рівняння у змінних y i z записується сукупністю розв’язком:

Враховуючи, що  з одержаних розв’язків з яких отримуємо дві сукупності диференційних рівнянь:
з одержаних розв’язків з яких отримуємо дві сукупності диференційних рівнянь:

Одже множина розв’язків вихідного диференціального рівняння складається з двох цілей інтегральних кривих  і
і  .
.
Розв’язок, який задовольняє початкові умови у(1)=1, у’(1)= -1 входить у другу сімю, яка виражається загальним інтегралом  . З цього загального інтеграла вилучаємо розвязок, що задовольняє задані початкові умови. Для цього маємо систему рівнянь для визначення
. З цього загального інтеграла вилучаємо розвязок, що задовольняє задані початкові умови. Для цього маємо систему рівнянь для визначення  і
і 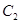 :
:

Таким чином, шуканий розв’язок задачі Коші має вигляд:

Задача 3. Проінтегрувати рівняння  знаючи, що
знаючи, що  є розв’язком відповідного однорідного рівняння.
є розв’язком відповідного однорідного рівняння.
Розв’язання.Приймемо  і обчислемо похожі
і обчислемо похожі 
 Підставимо вирази для
Підставимо вирази для 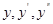 у рівняння:
у рівняння:

Після елементарних перетворень отримуємо рівняння:

або

Виконуємо заміну z’=u і маємо лінійне диференціальне рівняння першого порядку

Інтегруємо відповідне однорідне рівняння:

Загальний розв’язок лінійного неоднорідного рівняння стосовно функції u шукаємо у вигляді

Підготовимо цю функцію в неоднорідне рівняння і знайдемоС(х):

Отже, загальний розв’язок лінійного неоднорідного рівняння стосовно функції u записується у вигляді

Врахувавши, що  , одержуємо загальний розв’язок
, одержуємо загальний розв’язок

вихідного рівняння.
Задача 4. Розв’яжіть рівняння 

Задача 5. Розв’язати рівняння 
Дата добавления: 2020-01-07; просмотров: 76; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
