Геометричне тлумачення задачі Коші

Стр 1 из 3Следующая ⇒

Зміст

Вступ

Диференціальне рівняння вищого порядку

Зниження порядку диференціальних рівнянь другого порядку

Диференціальні рівняння є однорідними відносно функції у та її похідних і

Лінійні диференціальні рівняння другого порядку

Питання для перевірки

Тестові завдання

Задачі

Відповіді на тестові завдання

Розв’язок до задач

Охорона праці

Висновки

Література

Вступ

Для успішної участі у сучасному суспільному житті особистість повинна володіти певними прийомами математичної діяльності та навичками їх застосувань до розв’язання практичних задач. Певної математичної підготовки і готовності її застосовувати вимагає і вивчення багатьох навчальних предметів. Значні вимоги до володіння математикою у розв’язанні практичних задач ставлять сучасний ринок праці, отримання якісної професійної освіти, продовження освіти на наступних етапах. Тому одним з головних завдань цього тренінгу є забезпечення умов для досягнення кожним студентом практичної компетентності.

Прикладна спрямованість математичної освіти суттєво підвищується завдяки впровадженню комп’ютерів у навчання математики, повноцінному введенню ймовірносно-статистичної змістової лінії.

Мета: придбання знань, вмiнь та навичок, необхiдних для розв’язання та обчислення диференціальних рівнянь вищих порядків.

Завдання:

§ вивчення класичних і сучасних наближених методів розв’язання диференціальних рівнянь та їх систем;

§ придбання умінь використання методів розв’язання задач з початковими умовами та крайових задач для звичайних диференціальних рівнянь та диференціальних рівнянь з частинними похідними при моделюванні систем.

Студент повинен знати:

§ класифікацію наближених методів розв’язування диференціальних рівнянь та їх систем;

§ методи розв’язування трансцендентних, алгебраїчних і диференціальних рівнянь та їх систем;

§ методи чисельного інтегрування і диференціювання.

Студент повинен вміти: самостійно вибирати і обґрунтовувати раціональний метод розв’язування поставленої задачі.

Диференціальне рівняння вищого порядку

Диференційні рівняння вищого порядку стосовно функції у(х) має вигляд:

(1)

яке називають диференційованим рівнянням першого порядку, якщо рівняння (1) подано у вигляді:

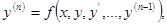(2)

та його називають диференційованим рівнянням першого порядку, яке є розв’язком відносно найстаршої похідної, або явним диференціальним рівнянням, або нормальним диференційованим рівнянням першого порядку.

Оскільки теоретичні поняття і методи інтегрування диференціальних рівнянь вищого порядку є споріднені для рівнянь різних порядків, то надалі ми обмежемось розглядом диференціальних рівнянь другого порядку:

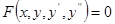(3)

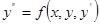(4).

Функція 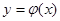називається розв’язком диференціального рівняння (3)чи (4) проміжну (a,b), якщо вона двічі не перервно диференційованa на цьому проміжку і будучи підставлена у рівняння, перетворює його у тотожність, тобто

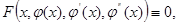x є (a,b)

або

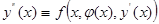
Графік функції 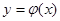називається при цьому інтегральною кривою диференціального рівняння (3) чи (4).

Зрозуміло, що інтегральна крива повинна міститися в області визначення функції F.

Наприклад, розв’язком диференційованого рівняння 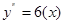є функція 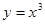на проміжку 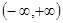, бо ця функція є двічі диференційована на цьому проміжутку і 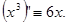Крім того, функція 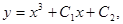де C_1,C₂- довільні сталі, є також розв’язком цього рівняння.

Аналогічно переконаємось, що функція 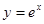і 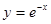є розвязками диференціального рівняння 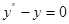на проміжку 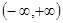, бо вони двічі диференційовані на цьому проміжку

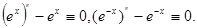
Розвязком цього рівняння є також функції де 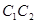- довільні сталі.

Далі будемо розглядпти основні поняття та означення для диференціального рівняння (4).

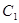Функція де і 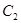довільні сталі називається загальним розв’язком диференційованого рівняння другого порядку, якщо вона є розв’язком цього рівняння для розв’язком функці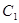ї і 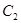і з якої за рахунок вибору значень цих сталих можна отримати будь-який розв’язок цього рівняння (за винятком може окремих).

Розвязок який отримуємо із загального диференціального рівняння 2-го порядку, мадаючи 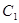і 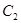певних числових значень, називається числовим розвязком цього рівняння.

Задача Коші. Практичних задач, які зводяться до диференціального рівняння другого порядку, потрібно відшукати розвязок цього рівняння, що задовольняє певні додаткові умови.

Найчастіше ними є умови Коші:

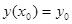
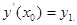(5)

Задача знаходження розвязку диференціального рівняння (4), який задовольняє умови (5), називається задачею Коші для цього рівняння. Цю задачу Коші записуватимемо коротко:

Геометрично, задача Коші для диференціального рівняння (4) полягає у знаходженні інтегральної кривої 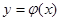цього рівняння. Яке проходить через точку 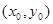і яка дотикається у цій точці до вектора, що утворює кут y, з додатним напрямком осі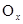

Геометричне тлумачення задачі Коші

Зрозуміло, що точки повинні лежати області визначення функції 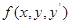, тобто області визначення диференціального рівняння (4).

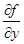Можна показати, що правильне таке твердження: якщо функція та її частинні похідні і є неперервні в деякому околі точки , то існує єдиний розв’язок 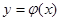задачі Коші (4) – (5), який визначений у певному околі точки .

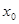Геометрично це означає, що при виконанні умов сформульованої теореми, через точну 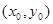проходить єдина інтегральна крива диференціального рівняння (4), яка замикається у цій точці до вектора, який утворює з додатним напрямом осі 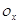кут .

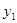З теореми існування та розв’язку задачі Коші для рівняння (4) випливає, що при виконанні умов теореми в деякому околі точки 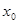існує загальний розв’язок 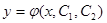цього рівняння, з розв’язком якого отримати розв’язок задачі Коші, визначивши значення сталих і 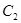із системи рівнянь:

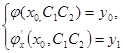(6)

Відзначемо, що система рівняння (6) завжди є розв’язком, бо існує розв’язок задачі Коші (4) – (5)

На практиці для диференціального рівняння другого порятку можуть бути задані інші умови замість умов Коші. Ними можуть бути крайові умови: 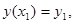і геометрична задача полягає у знаходженні інтигральної кривої диференціального рівняння (4), яка проходить через дві точки , .

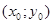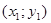Примітка. Якщодиференціального рівняння (3) має один розвязок відносно 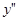, то воно рівносильне диференційномурівняню 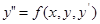, де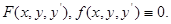

Якщо ж диференціальне рівняння (3) має декілька розв’язком відносно 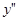, то воно рівносильне сукупності диференціальних рівнянь.

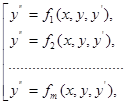де

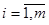
Дата добавления: 2020-01-07; просмотров: 59; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!