ТЕМА 2. ЛИНЕЙНАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
В статистическом анализе различают два типа регрессионных моделей: простую и множественную.
I . Парная (простая) регрессия
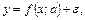 (2.1)
(2.1)
где y – эндогенная, x – экзогенная и 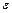 – случайная «шоковая» переменная, a – неизвестный вектор параметров модели.
– случайная «шоковая» переменная, a – неизвестный вектор параметров модели.
Под термином «шоковая» переменная в регрессии понимают не только случайные (переменные погрешности) модели, но и экзогенные (факторные) переменные, которые считаются несущественными (незначимыми) по степени влияния на эндогенную переменную. В инженерной литературе эта переменная называется шумом, чтобы отличить ее от понятия полезного сигнала модели, который формируют существенные экзогенные переменные.
По степени владения априорной информацией возникают различные задачи эконометрического анализа:
при неизвестной функции взаимосвязи 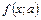 возникает задача подбора структуры (формы) модели, частными случаями которой являются модели с заданной функцией ( с точностью до неизвестных параметров a);
возникает задача подбора структуры (формы) модели, частными случаями которой являются модели с заданной функцией ( с точностью до неизвестных параметров a);
при заданной форме (функции 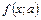 ) возникают задачи оценивания неизвестных параметров a, которые существенно облегчаются, если функция
) возникают задачи оценивания неизвестных параметров a, которые существенно облегчаются, если функция 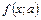 – линейная по параметрам a. Следует заметить, что нелинейность функции по экзогенным переменным не осложняет процесс (выбор методов) оценивания параметров. Например, модель:
– линейная по параметрам a. Следует заметить, что нелинейность функции по экзогенным переменным не осложняет процесс (выбор методов) оценивания параметров. Например, модель:

относится к классу линейных моделей по параметрам  и нелинейных относительно экзогенной переменной х;
и нелинейных относительно экзогенной переменной х;
|
|
|
при недоступности точного измерения экзогенной переменной возникает задача оценивания условной регрессии, для решения которой применяются методы и свойства условного математического ожидания из теории вероятностей. Если же исследователю точно известны измерения переменной х, то используется аппарат «классической» регрессии для решения задачи определения формы и параметров модели.
В эконометрике наиболее подробно изучен частный случай простой линейной регрессии, в которой линейность означает пропорциональную зависимость y от x посредством неизвестных параметров:
 (2.2)
(2.2)
где a 0 и a 1 – неизвестные параметры модели.
Примером модели (2.2) является модель макроэкономики, отражающая закон А. Оукена об обратной зависимости темпа роста ВНП от темпа роста уровня безработицы [3]:
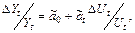
где 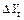 и
и 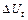 – абсолютные приросты объема ВНП
– абсолютные приросты объема ВНП 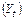 и уровня безработицы
и уровня безработицы 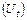 за определенный период времени t. Оценки параметров по данным американской статистики составили:
за определенный период времени t. Оценки параметров по данным американской статистики составили: 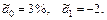
2. Модель множественной регрессии
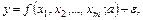 (2.3)
(2.3)
|
|
|
где описывается зависимость одной эндогенной переменной от m ( m >1) экзогенных переменных. Например, производственная функция Кобба-Дугласа в логарифмической форме принадлежит классу моделей типа (2.3):
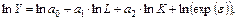
где Y, L, K – переменные, которые обозначают объем выпуска продукции, затрачиваемого труда и основных фондов соответственно; 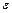 – шоковая (возмущающая) переменная, отражающая влияние других факторов на выпуск Y.
– шоковая (возмущающая) переменная, отражающая влияние других факторов на выпуск Y.
Благодаря случайной переменной 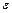 , математически описываемой случайной величиной, эндогенная переменная тоже является случайной величиной, поэтому задача восстановления зависимости y от
, математически описываемой случайной величиной, эндогенная переменная тоже является случайной величиной, поэтому задача восстановления зависимости y от 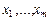 может быть решена лишь при многократных наблюдениях этих переменных, полученных в различные моменты времени
может быть решена лишь при многократных наблюдениях этих переменных, полученных в различные моменты времени  . Результаты статистических наблюдений помещают в специальную таблицу исходных данных:
. Результаты статистических наблюдений помещают в специальную таблицу исходных данных:
Номера наблюдений (t) | Наблюдаемые переменные | |||
| Эндогенная yt | Экзогенные | |||
| х1t | … | х mt | ||
| 1 | y1 | х11 | … | х m1 |
| 2 | y2 | х12 | … | х m2 |
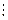
| 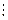
| 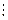
| 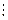
| |
| Т | yT | х1T | … | х mT |
Выделяются две основные задачи регрессионного анализа:
1) Установление формы взаимосвязи между переменными y и 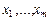 , т.е. подбор такой функции f, которая в определенном смысле оптимально характеризовала бы эту взаимосвязь.
, т.е. подбор такой функции f, которая в определенном смысле оптимально характеризовала бы эту взаимосвязь.
|
|
|
2) Оценивание неизвестных параметров регрессионной модели, проверка гипотез об их значимости и адекватности модели анализируемому экономическому объекту.
I. Решение этих задач начнем с более простой задачи оценивания параметров простой линейной регрессии, которое без потери общности можно применить и к оценке параметров множественной линейной регрессии вида:
 (
( 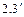 )
)
В статистической науке накоплен достаточно большой арсенал методов оценивания параметров регрессии, выбор которых зависит как от степени априорной информации, доступной исследователю, так и от критерия качества, согласно которому осуществляется оптимальный выбор оценок параметров. Наиболее часто используемыми методами оценивания являются:
¨ метод максимального правдоподобия (ММП), который строит оценки, доставляющие максимум функции правдоподобия, представляющий собой функцию распределения выборочных данных, которая предусматривает знание вида закона распределения переменных модели;
¨ байесовский метод оценивания, который максимизирует апостериорную плотность распределения вероятностей переменных модели и требует еще большей информации, чем предыдущий (ММП), состоящий в знании априорного распределения вероятностей неизвестных параметров;
|
|
|
¨ метод моментов, который находит оценки из решения системы уравнений, составленных приравниванием выборочных и теоретических начальных моментов;
¨ метод наименьших квадратов, который минимизирует сумму квадратов отклонений реальных наблюдений за эндогенной переменной от ее значения, рассчитанных по модели.
В последнее время интенсивно развиваются робастные и непараметрические методы оценивания параметров, которые существенно уменьшают требования к наличию априорной информации о виде распределения выборочных данных и к отсутствию выбросов (аномальных наблюдений).
Основным методом решения второй задачи в эконометрике является метод наименьших квадратов (МНК), который позволяет находить оценки, обеспечивающие максимальную точность (минимальную дисперсию) в классе несмещенных и линейно связанных с наблюдениями y оценками:
 (2.4)
(2.4)
где  – подстановочное значение эндогенной переменной от включения оценок неизвестных параметров
– подстановочное значение эндогенной переменной от включения оценок неизвестных параметров 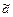 :
:
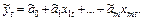
Тогда критерием качества оценивания по МНК будет сумма квадратов наблюдаемых отклонений реально зарегистрированных  и подстановочных значений
и подстановочных значений 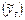 , обозначаемых символом
, обозначаемых символом 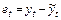 . Этот переход делает задачу оценивания реализуемой, т.к. значения случайной переменной
. Этот переход делает задачу оценивания реализуемой, т.к. значения случайной переменной 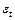 – не наблюдаемые в процессе регистрации статистических данных регрессионной модели – не могут участвовать в формировании критерия качества оценивания.
– не наблюдаемые в процессе регистрации статистических данных регрессионной модели – не могут участвовать в формировании критерия качества оценивания.
Однако метод наименьших квадратов обеспечивает оптимальные свойства МНК-оценкам лишь при выполнении следующих классических модельных предположений.
П.1. Отсутствие систематических ошибок наблюдений уравнения регрессии:

Другими словами, при операции усреднения переменных моделей, влияние случайной переменной исчезает.
П.2. Наблюдения организованы так, что случайные ошибки не коррелированны между собой:


П.3. Наблюдения производятся с одинаковой точностью, т.е. дисперсии случайных переменных одинаковы во все моменты измерения:

Предположение П.3 носит название гомоскедастичности.
П.4. Экзогенные переменные измеряются без ошибок, и в случае модели множественной регрессии их значения, полученные на протяжении всех моментов наблюдения, образуют линейно-независимые векторы.
П.5. Закон распределения вероятностей случайной переменной принадлежит к классу нормальных распределений с нулевым математическим ожиданием и дисперсией 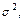 которая чаще всего неизвестна.
которая чаще всего неизвестна.
В рамках перечисленных модельных предположений решение задачи (2.4) может быть найдено как решение системы нормальных уравнений, которая для модели простой линейной регрессии имеет вид:
 (2.5)
(2.5)
Нетрудно получить решение системы (2.5) в явном виде:
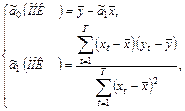 (2.6)
(2.6)
где 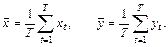
Дадим геометрическую иллюстрацию оценки параметров, приводящей к восстановлению взаимосвязи между  и
и 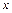 по МНК:
по МНК:
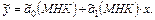
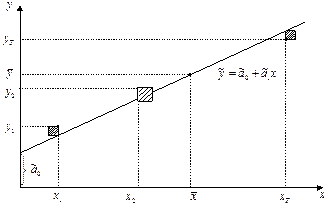
Рис. 3
На рис.3 показано, что прямая восстановленной по МНК зависимости y от x проходит через «центр тяжести» 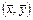 множества обрабатываемых пар данных
множества обрабатываемых пар данных 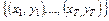 . Причем, оценка
. Причем, оценка  определяет отрезок, отсекаемый прямой
определяет отрезок, отсекаемый прямой  от оси ординат, а оценка
от оси ординат, а оценка 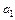 представляет собой тангенс угла наклона прямой
представляет собой тангенс угла наклона прямой  с осью абсцисс.
с осью абсцисс.
Перечислим важные свойства параметров простой линейной регрессии (ПЛР), полученных по МНК.
Свойство 1. Оценки параметров  и
и 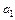 имеют нормальные вероятностные законы распределения и обладают свойством несмещенности.
имеют нормальные вероятностные законы распределения и обладают свойством несмещенности.
Для доказательства свойства 1 представим (без потери общности) модель ПЛР в центрированном относительно переменной x виде, с этой целью введем преобразование  , тогда
, тогда
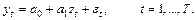
Тогда оценки (2.6) примут вид:
 (2.7)
(2.7)
Заметим, что
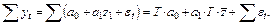
Вследствие того, что 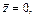 получим:
получим:
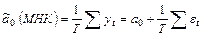 (2.8)
(2.8)
и (после усреднения оператором математического ожидания) окончательно будем иметь:
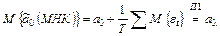 (2.9)
(2.9)
Соотношение (2.9) указывает на несмещенность 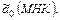
Вычислим дисперсию этой оценки:
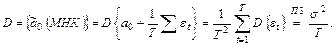
Окончательно учитывая аддитивность нормального распределения и связь (2.8) между случайными величинами 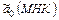 и
и 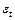 , замечаем, что оценки
, замечаем, что оценки 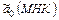 имеют нормальный закон распределения вероятностей со средним
имеют нормальный закон распределения вероятностей со средним  , дисперсией
, дисперсией  . Однако на практике дисперсия случайной переменной
. Однако на практике дисперсия случайной переменной 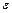 –
– 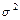 обычно неизвестна и ее заменяют несмещенной оценкой вида (величину s именуют SEE):
обычно неизвестна и ее заменяют несмещенной оценкой вида (величину s именуют SEE):
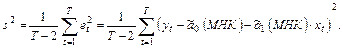 (2.10)
(2.10)
С учетом формулы (2.10) нетрудно определить доверительный интервал параметра  на основании известного из теории вероятностей факта, что величина
на основании известного из теории вероятностей факта, что величина  следует закону распределения Стьюдента с параметром Т–2, который соответствует числу степеней свободы, содержащемуся в исходных данных. В нашем случае (ПЛР) исходные данные связаны двумя параметрическими зависимостями, поэтому независимых данных насчитывается Т–2. Тогда, задавая доверительную вероятность
следует закону распределения Стьюдента с параметром Т–2, который соответствует числу степеней свободы, содержащемуся в исходных данных. В нашем случае (ПЛР) исходные данные связаны двумя параметрическими зависимостями, поэтому независимых данных насчитывается Т–2. Тогда, задавая доверительную вероятность 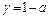 и определяя по таблицам закона Стьюдента квантиль
и определяя по таблицам закона Стьюдента квантиль 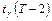 из условия
из условия 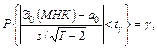 получим доверительный интервал для параметра
получим доверительный интервал для параметра 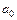 :
:
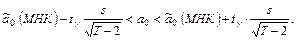 (2.11)
(2.11)
Проведем анализ вероятностных свойств оценки параметра 
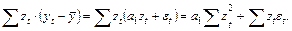
Отсюда
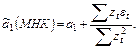 (2.12)
(2.12)
Подвергая равенство (2.12) оператору усреднения, получим:
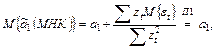
что подтверждает несмещенность оценки 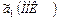 .
.
Вычисляя дисперсию оценки 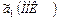 , будем иметь:
, будем иметь:

 .
.
Тогда можно сделать вывод о нормальности вероятностного распределения оценки 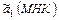 со средним
со средним  и дисперсией
и дисперсией 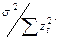
Доверительный интервал для параметра 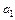 с надежностью
с надежностью  при неизвестной дисперсии
при неизвестной дисперсии 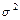 имеет вид:
имеет вид:
 .
.
Свойство 2. Фундаментальное свойство МНК формулируется в виде теоремы Гаусса-Маркова, отмечающей высокую степень близости МНК-оценок к искомым параметрам.
Теорема Гаусса-Маркова
МНК-оценки параметров линейной регрессии обладают наименьшими дисперсиями среди множества всех несмещенных и линейно-зависимых от эндогенных переменных оценок в рамках модельных предположений П1-П4.
Кроме задачи оценивания параметров в эконометрике часто представляет интерес задача о значимости параметров, т.е. задача проверки отделимости параметров регрессии от нуля, которая решается проверкой статистических гипотез при выполнении всех предположений модели П1-П5 [5; 11]:
 (2.13)
(2.13)
Решающее правило проверки гипотез (2.13) имеет вид следующего алгоритма:
если  где
где  – квантиль распределения Стьюдента с надежностью
– квантиль распределения Стьюдента с надежностью  , то отклоняют гипотезу
, то отклоняют гипотезу 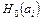 и делают вывод о существенности (значимости) параметра
и делают вывод о существенности (значимости) параметра 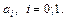
Наряду с проверкой гипотезы о значимости параметров регрессии важной задачей является проверка адекватности регрессионной модели, т.е. обоснованности выбора принятой в соответствии с моделью регрессии взаимосвязи  и
и 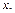
Мерой адекватности регрессии служит коэффициент детерминации, который вычисляется по формуле:
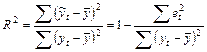 . (2.14)
. (2.14)
Справедливость правой части формулы (2.14) основана на тождестве:

в котором первое слагаемое описывает вклад в левую часть (TSS) регрессионного фактора (х) в зависимости от эндогенной переменной (ESS), а второе слагаемое – вклад остальных случайных факторов (RSS).
Заметим, что в эконометрических выводах часто применяется скорректированный (с учетом степеней свободы) коэффициент детерминации вида:
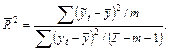 (2.15)
(2.15)
где  – число экзогенных переменных,
– число экзогенных переменных, 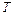 – число наблюдений.
– число наблюдений.
Решающее правило об адекватности моделей соответствует критерию проверки статистической гипотезы:
если 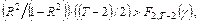 то отвергается гипотеза о неадекватности ПЛР.
то отвергается гипотеза о неадекватности ПЛР.
Здесь 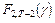 – квантиль порядка
– квантиль порядка  закона распределения Фишера.
закона распределения Фишера.
С помощью коэффициента детерминации можно сделать вывод о степени адекватности модели ПЛР:
а) если 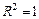 , то говорят, что ПЛР полностью отражает зависимость
, то говорят, что ПЛР полностью отражает зависимость 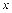 от
от  Геометрически это означает, что все наблюдаемые точки
Геометрически это означает, что все наблюдаемые точки 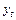 лежат на графике
лежат на графике  т.е.
т.е. 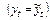 ,
, 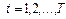
(рис. 4).

Рис. 4
б) если 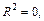 то делают вывод о том, что информация о значениях переменной
то делают вывод о том, что информация о значениях переменной 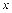 не влияет на изменение результирующего показателя
не влияет на изменение результирующего показателя  (рис.5):
(рис.5):

Рис. 5
Следовательно, в случае а) модель абсолютно адекватна, тогда как в условиях б) следует вывод о непригодности ПЛР.
По модели регрессии можно осуществить прогноз зависимой переменной вида:
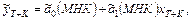
где 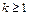 – параметр, указывающий на глубину прогноза,
– параметр, указывающий на глубину прогноза,  – планируемое в будущем моменте времени
– планируемое в будущем моменте времени 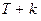 значение факторной переменной.
значение факторной переменной.
Доверительный интервал прогноза переменной  может быть представлен в виде [1]:
может быть представлен в виде [1]:
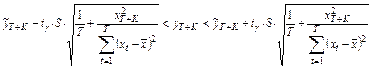 (2.16)
(2.16)
Изобразим графически доверительные границы:
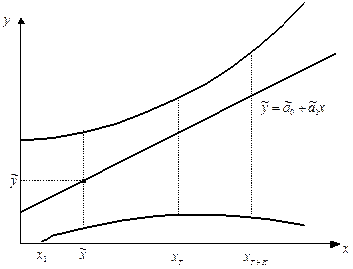
Рис. 6
Из рис.6 нетрудно видеть, что по мере увеличения горизонта прогнозирования (к >>1) увеличивается ширина доверительного интервала, что соответствует уменьшению точности прогнозируемого
значения 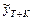 .
.
II . Модель множественной линейной регрессии вида (  ) удобно представить в векторно-матричной форме:
) удобно представить в векторно-матричной форме:
 (2.17)
(2.17)
где 
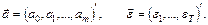
Здесь символ «'» обозначает оператор транспортирования.МНК-оценка вектора неизвестных параметров находится как решение задачи:
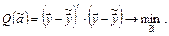 (2.18)
(2.18)
где 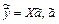 – вектор оценок множества неизвестных параметров
– вектор оценок множества неизвестных параметров 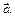
Решение задачи (2.18) сводится к нахождению решения системы «нормальных» уравнений:
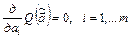
и имеет вид:
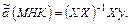 (2.19)
(2.19)
Все статические выводы, которые имели место для модели ПЛР, сохраняются в рамках модельных предположений П1 – П5 для модели множественной линейной регрессии.
Перечислим их в матричной форме:
1) МНК-оценки вектора параметров МЛР обладают свойством несмещенности, т.е.:
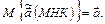
2) Несмещенная оценка дисперсии для случайной переменной 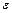 имеет вид:
имеет вид:

3) Дисперсия МНК-оценок параметров 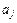 имеет вид:
имеет вид:
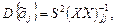
где символ 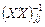 обозначает диагональный элемент, стоящий на пересечении j-й строки и j-го столбца матрицы
обозначает диагональный элемент, стоящий на пересечении j-й строки и j-го столбца матрицы  .
.
4) t-статистики для определения значимости параметров  имеют вид:
имеют вид:
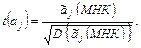
5) Доверительные интервалы параметров  имеют вид:
имеют вид:
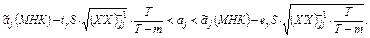
6) Доверительный интервал для прогноза  :
:
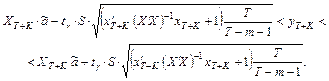
7) Адекватность МЛР проверяется с помощью F-критерия.
Если 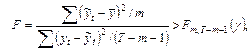
то гипотеза 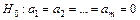 – неверна.
– неверна.
В противном случае – нет основания на данном уровне надежности  отвергать гипотезу
отвергать гипотезу 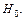
8) МЛР с линейными ограничениями на параметры:
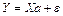 ,
,
где  (ЛОГ), В – заданная матрица полного ранга (
(ЛОГ), В – заданная матрица полного ранга ( 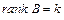 ), bK – заданный вектор размерности k .
), bK – заданный вектор размерности k .
Тождество (ЛОГ) определяет систему линейных ограничений на параметры, основными частными случаями которого являются:
Случай 1. 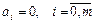 , для которого:
, для которого:
B =(0…010…0), b =0.
Случай 2. Два произвольных параметра совпадают:
ai = aj , 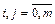 , для которого:
, для которого:
B =(0…010…-10…0), b =0.
Случай 3. Сумма нескольких параметров равна единице:
a 1 +…+ aq =1 ( q >1) , для которого:
B =(01…10…0), b =1.
Случай 4. Подмножество коэффициентов вектора параметров а равно нулю:
a 1 = a 2 =…= al =0, k = l , для которого:
B =( Il | Ol ) l , b = (0 l ) T
Формула оценки МНК-параметров МЛР с учетом линейных ограничений имеет вид:
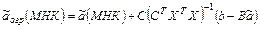 ,
,
где 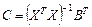 ,
, 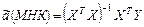 .
.
Пример 2.1. В теории формирования инвестиционного портфеля известна модель оценки капитальных активов (CAPM – Capital Asset Pricing Model), в рамках которой ожидаемая доходность акций некоторой компании определяется по регрессионной модели:
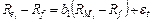 , (CAPM)
, (CAPM)
где 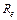 – ожидаемая доходность акций компании;
– ожидаемая доходность акций компании;
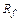 – доходность безрисковых ценных бумаг (государственные облигации);
– доходность безрисковых ценных бумаг (государственные облигации);
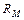 – доходность в среднем на рынке ценных бумаг.
– доходность в среднем на рынке ценных бумаг.
Тогда величина 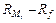 представляет собой рыночную премию за риск при вложении инвестируемого капитала в ценные бумаги;
представляет собой рыночную премию за риск при вложении инвестируемого капитала в ценные бумаги;
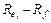 – премия за риск при вложении капитала в ценные бумаги данной компании. Значение параметра (бета-коэффициента)
– премия за риск при вложении капитала в ценные бумаги данной компании. Значение параметра (бета-коэффициента) 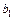 представляет собой индекс доходности данной компании и оценивается по МНК:
представляет собой индекс доходности данной компании и оценивается по МНК:
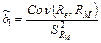 ,
,
где:
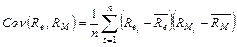 ;
;

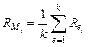 – средняя доходность акций на рынке ЦБ в период t;
– средняя доходность акций на рынке ЦБ в период t;
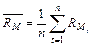 – доходность акций в среднем на рынке ЦБ за все наблюдаемые периоды (n);
– доходность акций в среднем на рынке ЦБ за все наблюдаемые периоды (n);
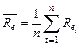 – средняя доходность акций компании e за все наблюдаемые периоды.
– средняя доходность акций компании e за все наблюдаемые периоды.
Тогда, если  , делают вывод о равенстве средней степени риска акций данной компании риску, сложившемуся на рынке в целом; если
, делают вывод о равенстве средней степени риска акций данной компании риску, сложившемуся на рынке в целом; если  , то ЦБ данной компании более рискованны, чем в среднем на рынке ЦБ.
, то ЦБ данной компании более рискованны, чем в среднем на рынке ЦБ.
Задача 2.1. Пусть эконометрическая модель зависимости зарплаты преподавателя от ряда факторов производительности труда имеет вид:
 ,
,
где 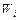 – оклад i-ого преподавателя в текущем учебном году;
– оклад i-ого преподавателя в текущем учебном году;
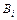 – число его опубликованных книг за весь период работы;
– число его опубликованных книг за весь период работы;
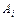 – число его опубликованных статей за весь период работы;
– число его опубликованных статей за весь период работы;
 – число его «выдающихся» статей за весь период работы;
– число его «выдающихся» статей за весь период работы;
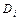 – число диссертаций, по которым им осуществлялось научное руководство за последние 5 лет;
– число диссертаций, по которым им осуществлялось научное руководство за последние 5 лет;
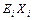 – стаж его педагогической работы.
– стаж его педагогической работы.
1. Проверьте соответствие знаков при коэффициентах модели вашим ожиданиям.
2. Если профессор имеет дополнительное время, чтобы написать книгу или две «солидные» статьи, или руководить тремя диссертациями, то что Вы ему порекомендуете выбрать?
3. Какие факторы кажутся Вам избыточными?
Задача 2.2. Пусть решается задача описания зависимости региональной зарплаты неквалифицированных рабочих от места работы
в определенном регионе с помощью следующей модели:

 ,
, 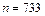 ,
,
где 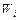 – почасовая зарплата i-ого рабочего;
– почасовая зарплата i-ого рабочего;
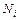 – качественная (дихотомическая) переменная;
– качественная (дихотомическая) переменная;

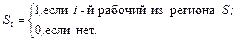
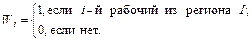
1.Какое условие модели, на Ваш взгляд, пропущено?
2.Какое из следующих утверждений наиболее корректно?
a) модель объясняет лишь 49 % вариаций относительно средней зарплаты рабочих по стране так, что эта модель неадекватна;
б) коэффициенты региональных переменных кажутся одинаковыми, так что эта модель неадекватна.
Задача 2.3. Рассмотрим модель удельного потребления мяса в США:
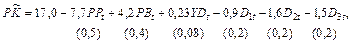
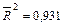 ,
, 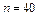 ,
,
где 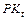 – удельное потребление мяса в t-м квартале;
– удельное потребление мяса в t-м квартале;
 – цена мяса в квартале t;
– цена мяса в квартале t;
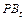 – цена заменителя мяса (соя) в квартале t;
– цена заменителя мяса (соя) в квартале t;
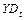 – располагаемый доход на душу населения в t-м квартале;
– располагаемый доход на душу населения в t-м квартале;
 – качественная переменная
– качественная переменная

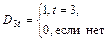
1. Оцените соответствие знаков первых 3 коэффициентов при экзогенных переменных Вашим ожиданиям.
2. Объясните смысл оценок сезонных факторов 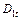 ,
, 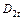 и
и 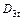 .
.
3. Если цены и доход в этой модели преобразовать из номинального масштаба в реальный, то как изменится данная модель (что следует добавить в перечень переменных)?
Задача 2.4. Эконометрическая модель зависимости Y от трех экзогенных переменных 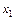 ,
, 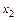 и
и 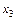 на основе 30 наблюдений имеет вид:
на основе 30 наблюдений имеет вид:

95 % – дов. границы 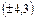
1. Заполните пропуски.
2. Что можно сказать о значимости коэффициентов регрессии на уровне значимости 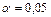 ?
?
Задача 2.5. Рассмотрим следующие данные, описывающие зависимость общего потребления 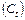 и дохода
и дохода 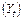 на конец периода
на конец периода  (в млрд руб.):
(в млрд руб.):

| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
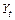
| 1831 | 1881 | 1883 | 1968 | 1909 | 2013 | 2123 | 2235 | 2332 | 2401 |
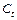
| 1666 | 1735 | 1749 | 1813 | 1755 | 1865 | 1945 | 2044 | 2122 | 2162 |
Предполагая линейную зависимость между C и Y
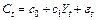 :
:
1. Оцените по табличным данным неизвестные параметры автономного потребления (  ) и предельной склонности к потреблению (
) и предельной склонности к потреблению (  ).
).
2. Если доход в следующем периоде ожидается на уровне  , найдите ожидаемое общее потребление
, найдите ожидаемое общее потребление 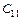 и доверительные границы, в которых будет содержаться этот прогноз с надежностью
и доверительные границы, в которых будет содержаться этот прогноз с надежностью 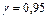 .
.
Задача 2.6. Для оценивания размера арендной платы за использование сервера была выбрана степенная модель:
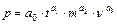 ,
,
где 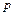 – ежемесячная арендная плата;
– ежемесячная арендная плата;
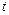 – быстродействие сервера;
– быстродействие сервера;
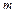 – объем оперативной памяти сервера;
– объем оперативной памяти сервера;
 – скорость обмена информацией.
– скорость обмена информацией.
Собранные данные о значениях переменных модели для 5 серверов представлены в таблице:
| № сервера | 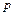
| 
| 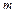
| 
|
| 1 | 6,5 | 690 | 4,8 | 10 |
| 2 | 8,3 | 3,5 | 16 | 1,75 |
| 3 | 0,875 | 675 | 4 | 8 |
| 4 | 22,5 | 12 | 131 | 0,75 |
| 5 | 47,0 | 0,8 | 262 | 0,75 |
1) Укажите ожидаемые знаки параметров  ,
, 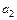 и
и 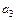 .
.
2) Линеаризуйте модель и оцените неизвестные параметры 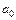 ,
, 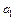 ,
, 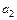 и
и 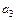 по МНК. Проведите анализ их значимости на уровне 5 %.
по МНК. Проведите анализ их значимости на уровне 5 %.
Задача 2.7. Рассмотрим следующую модель удельного потребления мясопродуктов вида (продолжение задачи 2.3):
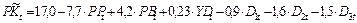 ,
,
(0,5) (0,4) (0,08) (0,2) (0,2) (0,2)
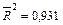 ,
,  ,
,
где 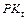 – удельное потребление мясопродуктов в течение периода t;
– удельное потребление мясопродуктов в течение периода t;
 – цена мясопродуктов в период t;
– цена мясопродуктов в период t;
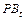 – цена товара – заменителя мясопродуктов в период t;
– цена товара – заменителя мясопродуктов в период t;
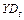 – располагаемый доход в период t;
– располагаемый доход в период t;
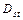 – переменная, выделяющая сезонный фактор в s-м квартале текущего года (s =1, 2, 3).
– переменная, выделяющая сезонный фактор в s-м квартале текущего года (s =1, 2, 3).
1. Проанализируйте адекватность модели.
2. Проведите проверку значимости полученных коэффициентов и модели в целом с надежностью  .
.
Задача 2.8. Теорема Гаусса-Маркова утверждает, что МНК-оценки являются несмещенными и эффективными (в смысле минимизации дисперсии). Что бы Вы предпочли:
оперировать несмещенной, но неэффективной оценкой или эффективной оценкой, но обладающей смещением (обоснуйте ваш выбор).
Задача 2.9. Укажите смысл каждого из следующих терминов:
| а) нулевая гипотеза; | б) альтернативная гипотеза; |
| в) ошибка первого ряда; | г) уровень значимости; |
| д) решающее правило; | е) критическое значение; |
| ж) t-критерий; | з) F-критерий; |
| и) мощность критерия. |
Задача 2.10. Проверьте адекватность модели при следующих полученных значениях решающей функции:
а) 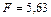 ; ;
| б)  ; ;
| в) 
|
| 4;30 | 3;24 | 5;60 |
на уровне значимости 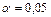 .
.
Задача 2.11. Зная следующие значения выборочных коэффициентов корреляции между двумя экзогенными переменными, примените t-критерий для проверки адекватности в нижеперечисленных обстоятельствах:
а)  ; ;
| 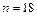 , ,
|  ; ;
| 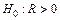 , ,
|
б)  ; ;
| 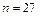 , ,
|  ; ;
| 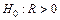 , ,
|
в)  ; ;
|  , ,
| 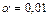 ; ;
| 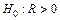 , ,
|
г) 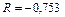 ; ;
| 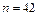 , ,
| 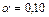 ; ;
| 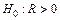 , ,
|
д) 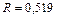 ; ;
| 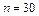 , ,
|  ; ;
| 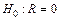 . .
|
Задача 2.12. Произведите анализ следующих эконометрических моделей по следующим характеристикам:
а) линейность по переменным;
б) линейность по параметрам:
1)  ;
;
2) 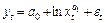 ;
;
3) 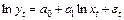 ;
;
4) 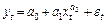 ;
;
5) 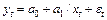 ;
;
6)  ;
;
7) 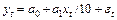 .
.
Укажите те из них, параметры которых могут быть оценены классическим методом наименьших квадратов.
Дата добавления: 2019-11-25; просмотров: 766; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
