Графическое представление рядов распределения.

Способы графического представления:

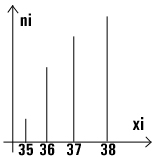
А) диаграмма в отрезках – совокупность вертикальных прямых /отрезков. Способ удобен для представления дискретных признаков при небольшом объеме совокупности.

Б) гистограмма – совокупность прилегающих друг к другу прямоугольников. Способ используется для изображения интервального ряда. На оси Х откладываются интервалы значения варианта. На каждом из них (на основании) строят прямоугольник. Его высота зависит от частоты встречаемости данной величины.

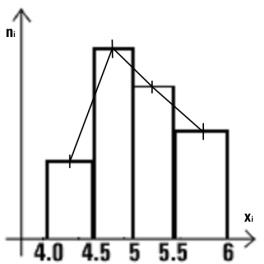
В) Полигон частот – ломаная линия, соединяющая точки, являющиеся серединами интервалов.

Г) Вариационные кривые в зависимости от значения распределения.

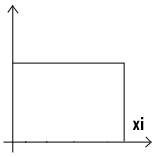Прямоугольное распределение объема совокупности

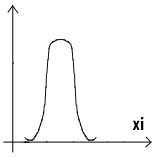Колоколообразное (= унимодальное)

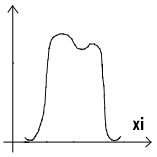Бимодальное

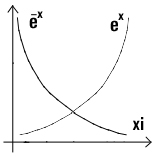Экспоненциальное

Основные меры положения и рассеяния частотного распределения.

Меры положения частотного распределения, их характеристика.

На практике ряды распределения описываются различными числовыми характеристиками (мерами).

1. Мода (Мо) – это варианта, наиболее часто встречающаяся в совокупности (= модальное значение).

2. Медиана (Ме) – это величина, делящая ранжированный ряд на 2 равные части. Так же она делит площадь под кривой распределения. Для того, чтобы определить Ме надо ранжировать ряд (в порядке возрастания), вычислить номер, под которым стоит медиана. N/2 – Для четных, (N+1)/2 – Для нечетного количества объектов

3. Средняя арифметическая простая – это частное деление суммы всех значений признака на их общее число объектов

X=(X1+X2+X3…+Xn)/N

Сумма всех <+> и <–> отклонений от х равно «0».

Среднюю арифметическую простую вычисляют для неупорядоченных рядов в тех случаях, когда каждая варианта встречается 1 раз.

4. Средняя взвешенная. Если в совокупности отдельные варианты встречаются неоднократно, то вычисляется средняя взвешенная – это величина, полученная суммированием произведений числовых значений вариант на их частоты с последующим делением суммы на количество всех вариант.

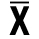= (х1n1+x2n2+x(n)n(n))/N x1n1+y2n2

5. Средняя квадратическая используется, если признаки выражаются мерами площади. Пример: размер колонии микробов, листовых пластинок.

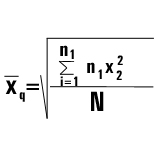
Средняя гармоническая, кубическая, геометрическая

Меры рассеяния частотного распределения. Его характеристика.

Разброс числовых значений вариант (генеральной, выборочной совокупности) относительно средних значений характеризуется мерами рассеяния.

1. Лимит – минимальная и максимальная варианта совокупности. (Xmin, Xmax)

2. Вариационный размах – разность между максимальным и минимальным значением R=Xmax-Xmin

3. Индивидуальное отклонение – разность между числовым значением варианты и средним арифметическим всей совокупности Di=X-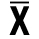

4. Дисперсия – мера рассеяния, полученная суммированием квадратов индивидуальных отклонений и последующим делением суммы на объем совокупности.

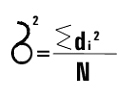
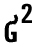- для генеральной

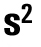- для выборочной совокупности

Если число объектов менее 30, то рассчитывается исправленная дисперсия (Сигма с крышей)

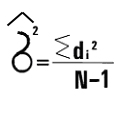
Где N-1 – число степеней свободы. Это число на 1 меньше, чем весь объем свободности

5. Стандартное (среднее квадратичное) отклонение. Эта мера рассеяния, равная корню квадрата дисперсии, S = корень квадратный из 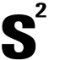. Чем сильнее варьирует признак, тем больше величина среднего квадратного отклонения.

6. Коэффициент вариации - мера рассеяния равна, отношению стандартного отклонения к средней арифметической V=(S/X)100%

При нормальном распределении коэффициент вариации не > 50%, а часто гораздо ниже (приблизительно 20%).

Механические волны, их виды.

Последовательное отклонение колеблющейся точки от положения равновесия то в одну, то в другую сторону называется механическим колебанием. Распространяющееся в упругой среде механические колебания называются механической волной. По направлению колебаний условных частиц среды различают продольные и поперечные волны.

Продольная волна – возникает тогда, когда направление колебания частиц среды совпадает с направлением распространения волны (в твёрдых, жидких и газовых средах).

Поперечная волна – если направление колебания частиц перпендикулярно направлению распространения волны (в твёрдых телах).

Дата добавления: 2019-11-25; просмотров: 484; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!