Основные понятия описательной статистики.

⇐ ПредыдущаяСтр 2 из 19Следующая ⇒

Генеральная совокупность – подлежащая изучению совокупность однородных элементов, которая характеризуется некоторым признаком. Например, нас интересует распространенность данного заболевания в определенном регионе, тогда генеральная совокупность, это все население региона. Если необходимо выразить мужчин и женщин отдельно по этому заболеванию, то получаем 2 генеральные совокупности.

Количество объектов, входящих в генеральную совокупность называется объемом генеральной совокупности (N). Генеральную совокупность можно изучать по некоторой ее части.

Выборочная совокупность - часть генеральной совокупности, выбираемая для статистической обработки (выборка) ( объем выборки -n). Свойства объектов выборки должны соответствовать свойствам генеральной совокупности. Результаты исследования некоторого признака генеральной совокупности, будут более надежны, если выборку образовывать случайным образом. Элементы выборки берутся наугад. Каждый объект может попасть в выборку с одинаковой вероятностью. Главным вопросом является: как определить объем выборки, необходимой для получения необходимого результата.

Варианта – значение признака для каждого элемента выборки (х). Признаки могут быть качественными и количественными. Количественные делятся на непрерывные (масса тела) и дискретные (количество волос). Признак, имеющий значение от одного объекта к другому называется варьирующимся. Если количественный признак лежит в интервале – интервальный.

Частота – количество объектов с конкретным числовым значением признака

xi 35 36 37 38 39 40 41

ni (pi): 2 4 5 6 7 7 2

Частность или относительная частота – доля варианта с данным значением признака (ni/n)

Выборки, их виды и требования к ним.

Для того чтобы получить исчерпывающую информацию о состоянии генеральной совокупности нужно учесть весь ее состав без исключения. Но не всегда есть возможность или необходимость прибегать к сплошному исследованию. В целях экономии времени и средств, анализу подвергается часть совокупности выборки, по ней судят о состоянии всей совокупности в целом.

Если число объектов менее 30, то выборка называется малой. В зависимости от способов формирования, выборки бывают повторные – с возвратом, не повторные – без возврата

Требования к выборкам:

А)Рандомизация - каждая варианта генеральной совокупности имеет одинаковую вероятность для попадания в выборку.

Б) Репрезентативность – состав и структура выборки должны соответствовать составу и структуре генеральной совокупности.

	Генеральная совокупность	Выборочная
Объем	N	n
Среднее значение	M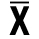
Дисперсия		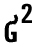S в квадрате
Стандартное отклонение		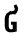S

Дата добавления: 2019-11-25; просмотров: 548; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!