Некоторые практические приложения
Лекция 4
Ранее была получена система уравнений:
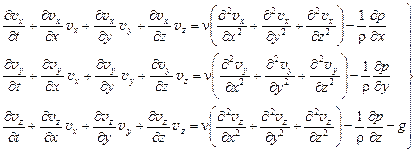(7.1)
Уравнения (7.1) есть дифференциальные уравнения Навье[1] – Стокса[2] движения вязкой жидкости, являющиеся математическим описанием полей скоростей и давлений в подвижной среде.
Конечно же, мы повсеместно имеем дело с реальными жидкостями.
Но многие закономерности поведения жидкостей удобно изучать на идеализированной модели — модели идеальной жидкости.
Дифференциальные уравнения Эйлера
Движения идеальной жидкости
Идеальная жидкость — воображаемая жидкость, обладающая следующими свойствами:
1. Она не оказывает сопротивления движению, то есть она не обладает внутренним трением (m = 0).
2. Она абсолютно несжимаема, то есть её объём, а значит, и плотность не зависят от давления ír ¹ ¦(p)ý.
3. Она не изменяет объём с изменением температуры ír ¹ ¦(Т)ý.
Так как идеальная жидкость не обладает внутренним трением, то в её потоке поля скоростей и давлений будут описываться системой дифференциальных уравнений:
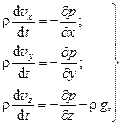(8.1)
где проекции ускорений на соответствующие оси координат записаны в «сжатой» форме.
Эти уравнения впервые были получены в 1755 году Леонардом Эйлером и называются дифференциальными уравнениями Эйлера движения идеальной жидкости.
Если жидкость неподвижна, то уравнения (8.1) упрощаются до вида:
|
|
|
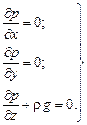(8.2)
Уравнения (8.2) называются дифференциальными уравнениями Эйлера покоя (статики) жидкости.
Леонард Эйлер родился 15 апреля 1707 года в швейцарском городе Бáзель в семье сельского пастора. Получив неплохое домашнее образование, Эйлер поступил в старшие классы гимназии и в то же время начал посещать лекции по математике в университете. Талант юного математика был замечен Иоганом Бернулли, который начал заниматься с ним индивидуально.
В 17 лет Эйлер уже получил степень магистра искусств.
В 1727 году Эйлер прибыл по приглашению в только что учреждённую Петербургскую Академию наук, где сначала стал адъюнктом, а в 1731 году (в возрасте 24 лет!) – профессором по математике. В Петербурге Эйлер жил и работал с 1727 по 1741 г. и с 1766 г. до конца жизни.
Эйлер привнёс бесценный вклад в развитие Российской науки. За годы работы в России он подготовил около 400 научных работ; полное собрание его сочинений составляет 72 тома.
Леонард Эйлер был не только талантливым и плодотворным учёным, но и человеком самоотверженным. Вот только один факт из его биографии.
|
|
|
В 1738 году срочно потребовалось провести трудоёмкие, астрономические расчёты для составления карт Российской Империи. Группа академиков требовала на их выполнение несколько месяцев… Блестящий вычислитель, Леонард Эйлер сделал всю работу за трое суток. Но какой ценой! В результате осложнения после тяжёлого нервного переутомления он потерял зрение правым глазом (когда ему было всего-то 30 лет), а постепенное развитие катаракты на левом глазу привело к тому, что в 59 лет он окончательно ослеп. Но, как в литературе Гомер, так в математике Эйлер был подлинно «слепец всевидящий».
Эйлер скончался в 1783 году и похоронен в Петербургском некрополе.
Для решения тех или иных задач гидравлики дифференциальные уравнения Эйлера следует проинтегрировать.
Интегрирование дифференциальных уравнений Эйлера движения идеальной жидкости приводит к уравнению Бернулли.
Уравнение Бернулли
Будем считать, что имеет место такое движение жидкости, при котором давление в какой-либо точке пространства, занятого идеальной жидкостью, с течением времени не изменяется.
Для выполнения процедуры интегрирования уравнений Эйлера (8.1) предварительно умножим каждое уравнение, соответственно, на v x, v y и v z. Тогда интегрированию подлежат уравнения вида:
|
|
|
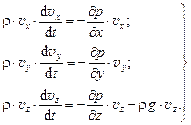(9.1)
Поскольку компоненты скоростей можно представить в виде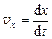 
, 
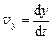и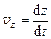 
, то соответствующая замена в правых частях уравнений и умножение всех слагаемых на dt приводит к системе:
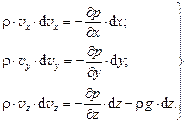(9.2)
Просуммируем правые и левые части всех трёх уравнений:
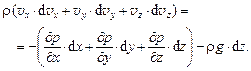(9.3)
Преобразуем это уравнение.
Его левая часть может быть представлена в виде:
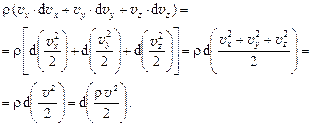(9.4)
В соответствии с допущением о неизменности давления во времени, то есть, считая, что p =¦(x, y, z), имеем выражение для полного дифференциала этой функции:
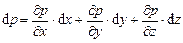. (9.5)
Тогда, с учётом (9.4) и (9.5), уравнение (9.3) может быть записано в виде:
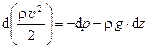, (9.6)
или
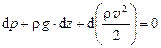, (9.7)
или, заменяя сумму дифференциалов дифференциалом суммы,
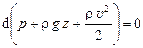. (9.8)
|
|
|
Интегрируя это уравнение, получаем:
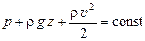. (9.9)
Уравнение (9.9) называется «интеграл Бернулли» или «уравнение Бернулли для элементарной струйки идеальной жидкости».
Даниил Бернулли принадлежал к семье известных швейцарских учёных. Он родился в 1700 году в Гронингене (Нидерланды), а вскоре семья Иоганна Бернулли – отца Даниила (и учителя Леонарда Эйлера(!)) – переехала в Базель, где Даниил сначала окончил гимназию, а затем изучал философию и логику в местном университете. Уже в 16 лет он получил степень магистра философии, в 21 год – степень лиценциата медицины. В это же время он опубликовал свою первую серьёзную научную работу – книгу «Математические упражнения».
В 1725 году Даниил вместе с братом Николаем прибыл по приглашению формировавшейся Академии Наук в Петербург.
8 лет работал Даниил Бернулли в Петербургской Академии, и это были годы наибольшего творческого подъёма. Однако, и покинув Россию, Д. Бернулли не прерывал связи с Петербургской Академией Наук, но уже в качестве её иностранного члена. В целом в изданиях Академии вышло 50 работ Д. Бернулли из 75 его научных трудов.
Именно в Петербурге Бернулли подготовил первый вариант рукописи своего главного труда: «Гидродинамика или записки о силах и движении жидкости». Кстати, этой работой Д. Бернулли ввёл в науку термин "гидродинамика".
Окончательный вариант этой книги был опубликован на латинском языке в 1738 году, в Страсбурге. Однако ещё в 1726 году Даниил Бернулли выступил с докладом на одном из заседаний Петербургской Академии Наук, и в этом докладе, среди прочего, был опубликован ставший теперь классическим принцип гидродинамики, согласно которому:
«в струе воды или воздуха давление велико, если скорость мала, и давление мало, если скорость велика».
Уравнение Бернулли является, по существу, одной из форм закона сохранения энергии.
Энергетический смысл слагаемых уравнения Бернулли становится очевидным из следующих рассуждений, приводимых применительно к элементарной частице жидкости объёмом dV, или массой dm = r×dV, или весом dG = dm×g = r×g ×dV.
Для того чтобы поднять (переместить) на высоту z элементарную частицу жидкости объёмом dV, необходимо произвести работу против силы тяжести, равную
W = -dG×z = -r×g×dV×z. (9.10)
При этом на эквивалентную величину увеличивается потенциальная энергия частицы:
Еп = -W = +r×g×dV×z . (9.11)
Следовательно, удельная (отнесённая к единице объёма) потенциальная энергия положения будет определяться значением:
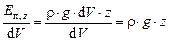, [Дж/м3] = [Па]. (9.12)
За счёт давления р элементарная частица жидкости объёмом dV может быть поднята на высоту h = p/(r×g). При этом производится работа против силы тяжести, равная: -dG×h = -r×g×dV×h , и потенциальная энергия частицы увеличивается на эквивалентную величину:
+r×g×dV×h = r×g ×dV×p/(r×g) = dV×p. (9.13)
Следовательно, удельная (отнесённая к единице объёма) потенциальная энергия давления будет определяться значением:
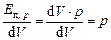, [Дж/м3] = [Па]. (9.14)
Очевидно, первые два слагаемые уравнения Бернулли в сумме определяют удельную потенциальную энергию элементарной частицы жидкости.
Наконец, элементарная частица жидкости массой dm = r×dV, движущаяся со скоростью v, обладает кинетической энергией:
Eк = dm×v2/2 = r×dV×v2/2. (9.15)
Следовательно, удельная (отнесённая к единице объёма) кинетическая энергия элементарной частицы будет определяться значением:
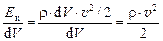, [Дж/м3] = [Па]. (9.16)
Величина rv2/2 именуется также «динамическое давление».
В соответствии с уравнением Бернулли сумма потенциальной и кинетической энергий элементарной струйки остаётся неизменной во всех сечениях.
Если каждое слагаемое уравнения (9.9) разделить на ускорение свободного падения g, то можно получить уравнение Бернулли в форме:
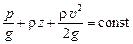, (9.17)
где каждое слагаемое уравнения есть удельная энергия единицы массы жидкости.
Наконец, если каждое слагаемое уравнения (9.9) разделить на постоянное произведение r×g, то получим уравнение Бернулли в форме:
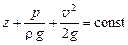, (9.18)
где каждое слагаемое уравнения есть удельная энергия единицы веса жидкости, а именно:
z — нивелирная (геометрическая) высота расположения сечения элементарной струйки жидкости над некоторой плоскостью сравнения, или удельная потенциальная энергия положения, [м] = [Дж/Н];
p/(r×g)— пьезометрическая высота, пропорциональная давлению в рассматриваемом сечении, или удельная потенциальная энергия давления столба жидкости, [м] = [Дж/Н];
v2/2g — высота столба жидкости, эквивалентная высоте, с которой в вакууме должна свободно (без начальной скорости) упасть элементарная частица жидкости, чтобы приобрести скорость v, или удельная кинетическая энергия, [м] = [Дж/Н].
И вновь отмечаем, что для элементарной струйки идеальной жидкости удельная энергия есть величина постоянная, одинаковая во всех сечениях струйки.
В гидравлике удельная энергия единицы веса жидкости называется «гидравлическим напором», или просто – «напором», и обозначается символом Н (от англ. head – напор).
Тогда величины z, p/(r×g) и v2/2g могут рассматриваться как, соответственно, геометрический напор, пьезометрический напор и динамический напор жидкости. И уравнение Бернулли показывает, что при установившемся движении идеальной жидкости сумма геометрического, пьезометрического и динамического напоров в каждом поперечном сечении элементарной струйки есть величина постоянная, то есть Н = const.
В дополнение к сказанному заметим, что при прекращении движения, то есть при v = 0, уравнение Бернулли обращается в основное уравнение гидростатики:
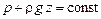. (9.19)
Некоторые практические приложения
Дата добавления: 2019-11-25; просмотров: 113; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!