Расчет математической модели равномерности выхода исследуемого материала из шихтового бункера БЗУ лоткового типа в колошниковое пространство доменной печи
После реализации плана экспериментов необходимо построить математическую модель, выявляющую коэффициент равномерности выхода коксового орешка из шихтового бункера БЗУ от выбранных факторов.
Коэффициенты уравнения 2.2 рассчитываются по упрощенным формулам [2, 3]:
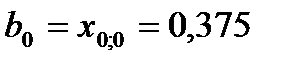 (3.1)
(3.1)
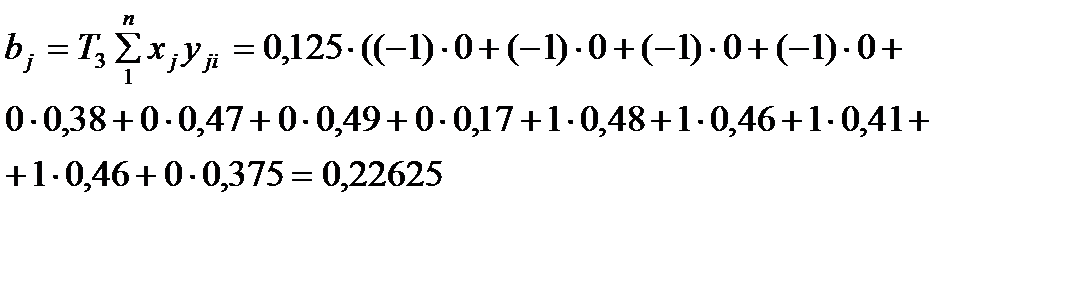 (3.2)
(3.2)
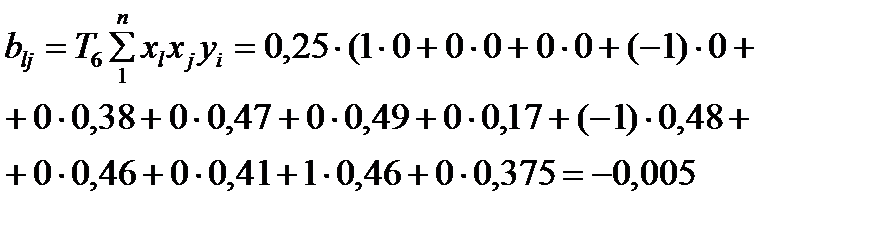 (3.3)
(3.3)
 (3.4)
(3.4)
где:
Ti – расчетный коэффициент (табл. 3.1) [2, 3].
Таблица 3.1
Значения Ti для плана Бокса-Бенкина
| Коэффициент Ti | Значение | Коэффициент Ti | Значение |
| T1 | - | T6 | 0,25 |
| T2 | 0,5 | T7 | 1,0 |
| T3 | 0,125 | T8 | 0,35355 |
| T4 | 0,25 | T9 | 0,6615 |
| T5 | 0,1875 | T10 | 0,5 |
Для проверки полученных коэффициентов уравнения на значимость, определяется критерий Стьюдента (t). Коэффициент значим, если расчетное значение t – критерия больше или равно табличному 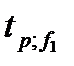 с уровнем значимости p, числе степеней свободы f1, с которым определена дисперсия S2y и следовательно S2b, [5]:
с уровнем значимости p, числе степеней свободы f1, с которым определена дисперсия S2y и следовательно S2b, [5]:
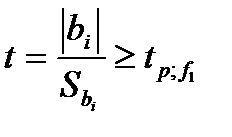 , (3.5)
, (3.5)
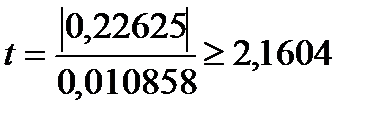
где:
bi – величина коэффициента регрессии;
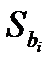 – среднеквадратическое отклонение коэффициента регрессии.
– среднеквадратическое отклонение коэффициента регрессии.
При многофакторных моделях значения дисперсии коэффициентов в уравнении регрессии можно определить по следующей формуле [5]:
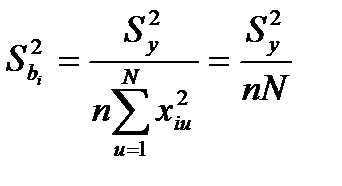 , (3.6)
, (3.6)

Табличное значение критерия Стьюдента приведено в приложении 2.
Проверка адекватности математической модели
Полученные модели, определяющие коэффициент равномерности поступления коксового орешка из бункера БЗУ в колошниковое пространство, описанные уравнениями 2.16 и 2.17 необходимо проверить на адекватность экспериментальным данным. Для этого использовали критерий Фишера – F [6]:
|
|
|
 , (4.1)
, (4.1)
где:
S2y – дисперсия опыта, определенная с числом степеней свободы f1;
S2ад – дисперсия адекватности, определенная с числом степеней свободы f2.
Дисперсия адекватности оценивает разброс опытных значений y относительно значений, предсказываемых уравнением регрессии 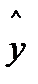 . В общем виде
. В общем виде 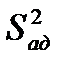 рассчитывается по формуле:
рассчитывается по формуле:
, 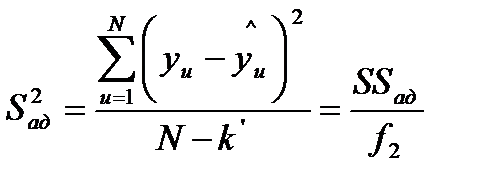 (4.2)
(4.2)
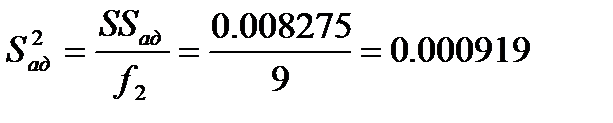
где
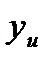 – опытные значения функции цели в u-м опыте;
– опытные значения функции цели в u-м опыте;
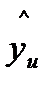 – значения, предсказываемые уравнением регрессии в u-м опыте;
– значения, предсказываемые уравнением регрессии в u-м опыте;
k’ – число незначимых коэффициентов уравнения (включая b0).
Гипотезу об адекватности уравнения принимали в том случае, когда расчетное значение F – критерия не превышает табличного, для выбранного уравнения значимости p:
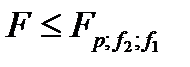 ,
,
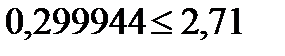
(4.3)
где:
F – расчетное значение критерия Фишера;
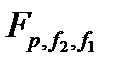 – табличное значение критерия Фишера (Приложение 3);
– табличное значение критерия Фишера (Приложение 3);
p – уровень значимости;
f1 – число степеней свободы, с которым определялась S2y и коэффициент Стьюдента;
Для объяснения разброса значений переменной 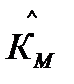 относительно среднего необходимо определить коэффициент детерминации R2 равный 0,99.
относительно среднего необходимо определить коэффициент детерминации R2 равный 0,99.
|
|
|
Анализ результатов
Для анализа полученных данных необходимо графически отобразить степень влияния исследуемых факторов, на коэффициент равномерности поступления исследуемого материала в колошниковое пространство доменной печи. Проанализировав зависимости необходимо выбрать рациональный режим загрузки исследуемого материала.
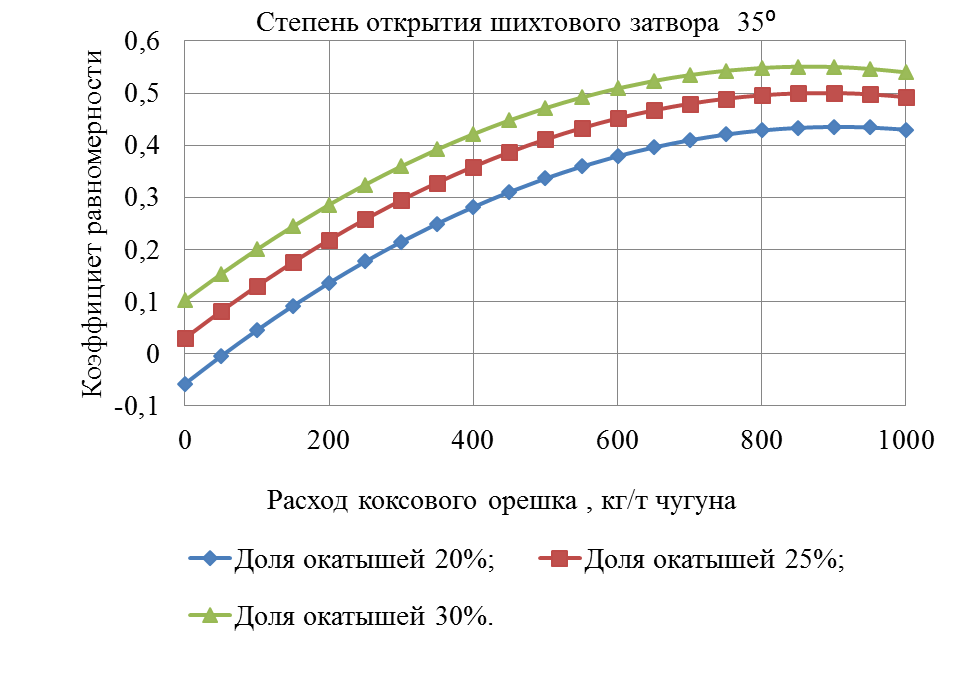
Рисунок 1 – Зависимость коэффициента равномерности от расхода коксового орешка.
На рисунке 1 зависимости коэффициента равномерности от расхода коксового орешка и доли окатышей от железорудной части шихты 20,25, 30% при угле открытия шихтового затвора 35 ̊является криволинейной возрастающей до расхода коксового орешка 850 кг/т чугуна, с 850 до 1000 кг/т чугуна – криволинейной убывающей. При доле окатышей от железорудной части шихты 20,25, 30% расходе коксового орешка 850 кг/т чугуна коэффициент распределения 0,433375; 0,499625; 0,5485 – точки экстремума соответственно.
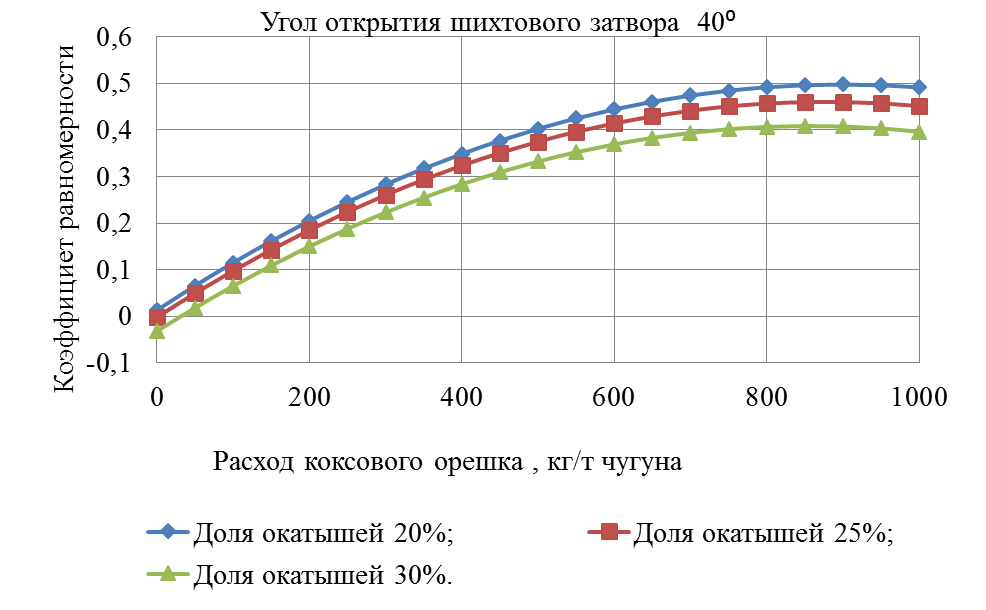
Рисунок 2 – Зависимость коэффициента равномерности от расхода коксового орешка
На рисунке 2 зависимости коэффициента равномерности от расхода коксового орешка и доли окатышей от железорудной части шихты 20,25, 30% при угле открытия шихтового затвора 40 ̊является криволинейной возрастающей до расхода коксового орешка 800 кг/т чугуна, с 800 до 1000 кг/т чугуна – криволинейной убывающей. При доле окатышей от железорудной части шихты 20,25, 30% расходе коксового орешка 800 кг/т чугуна коэффициент распределения 0,496125; 0,459875; 0,40675 – точки экстремума соответственно.
|
|
|
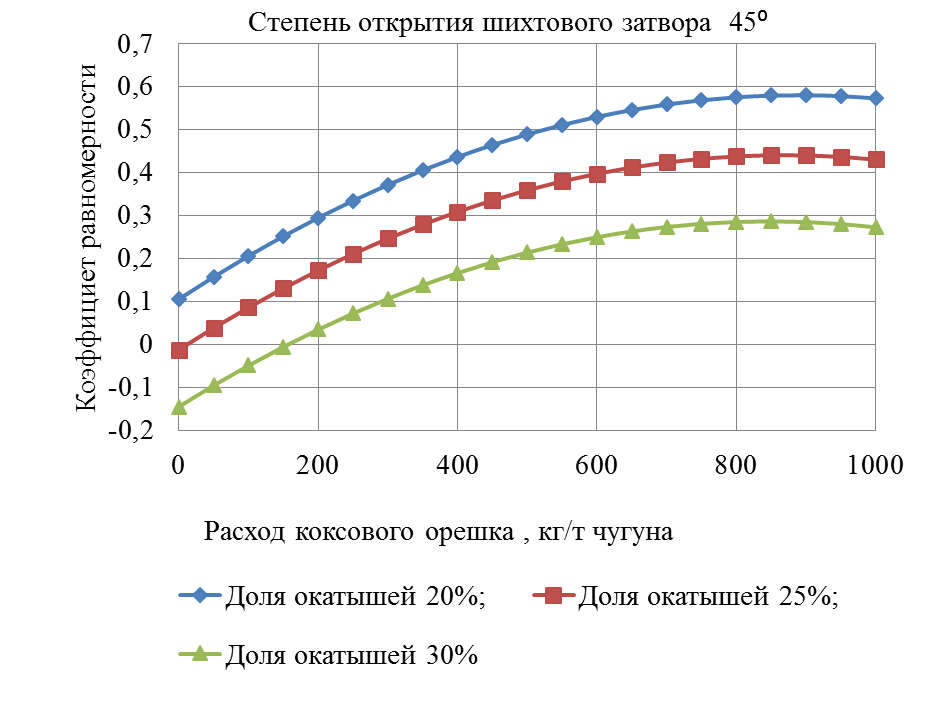
Рисунок 3 – Зависимость коэффициента равномерности от расхода коксового орешка.
На рисунке 3 зависимости коэффициента равномерности от расхода коксового орешка и доли окатышей от железорудной части шихты 20,25, 30% при угле открытия шихтового затвора 45 ̊является криволинейной возрастающей до расхода коксового орешка 800 кг/т чугуна, с 800 до 1000 кг/т чугуна – криволинейной убывающей. При доле окатышей от железорудной части шихты 20,25, 30% расходе коксового орешка 800 кг/т чугуна коэффициент распределения 0,578875; 0,4375; 0,285 – точки экстремума соответственно.
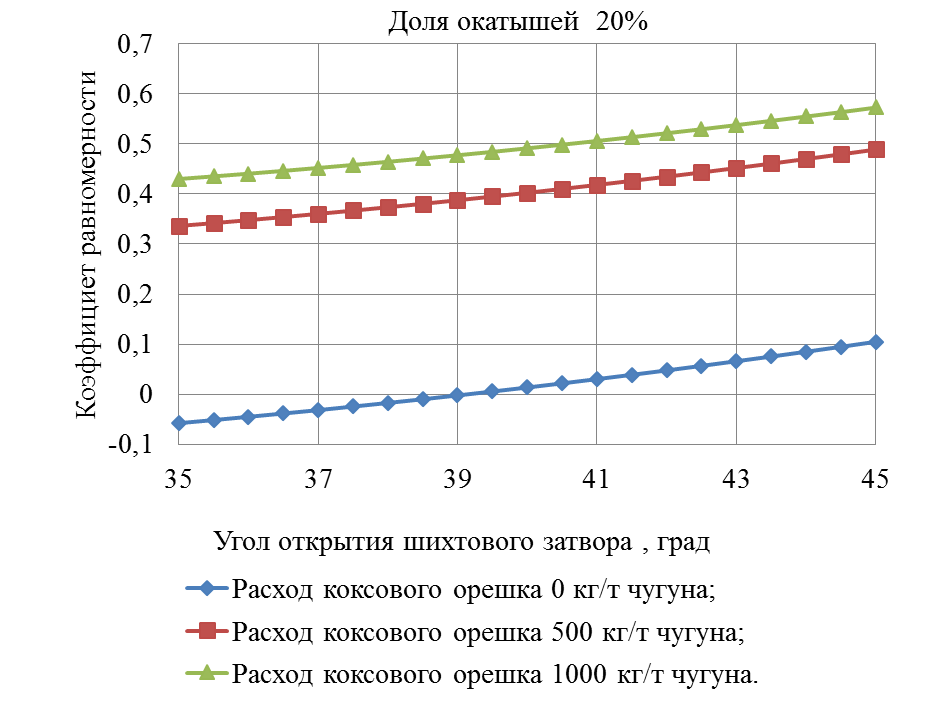
Рисунок 4 – Зависимость коэффициента равномерности от угла открытия шихтового затвора
На рисунке 4 зависимости коэффициента равномерности от угла открытия шихтового затвора и расходе коксового орешка при доле окатышей от железорудной части шихты 20% является криволинейной возрастающей.
|
|
|
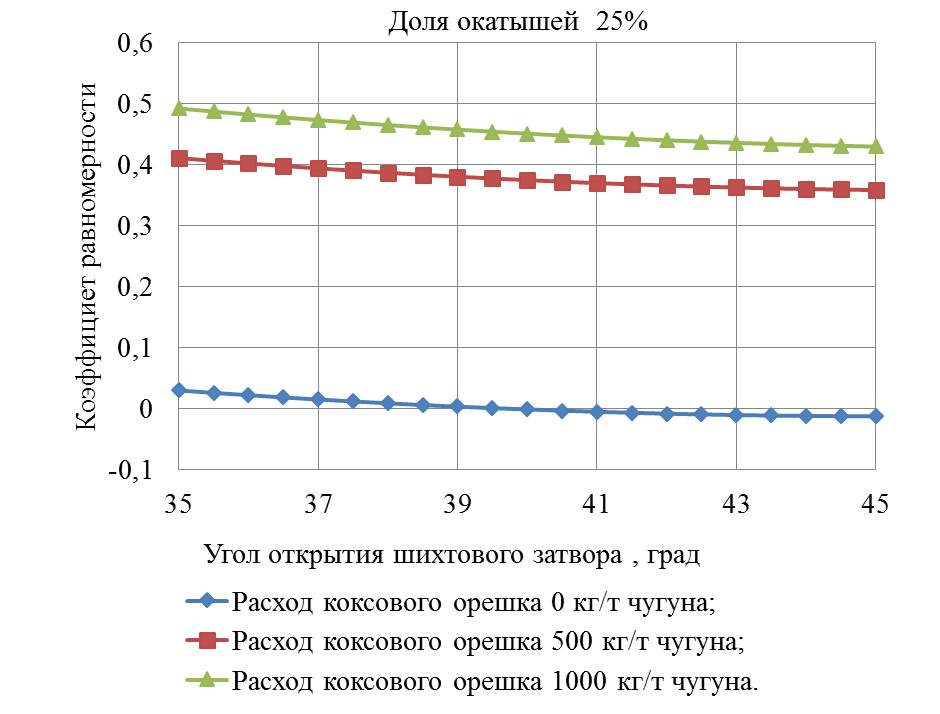
Рисунок 5 – Зависимость коэффициента равномерности от угла открытия шихтового затвора
На рисунке 5 зависимости коэффициента равномерности от угла открытия шихтового затвора и расходе коксового орешка при доле окатышей от железорудной части шихты 25% является криволинейной убывающей.
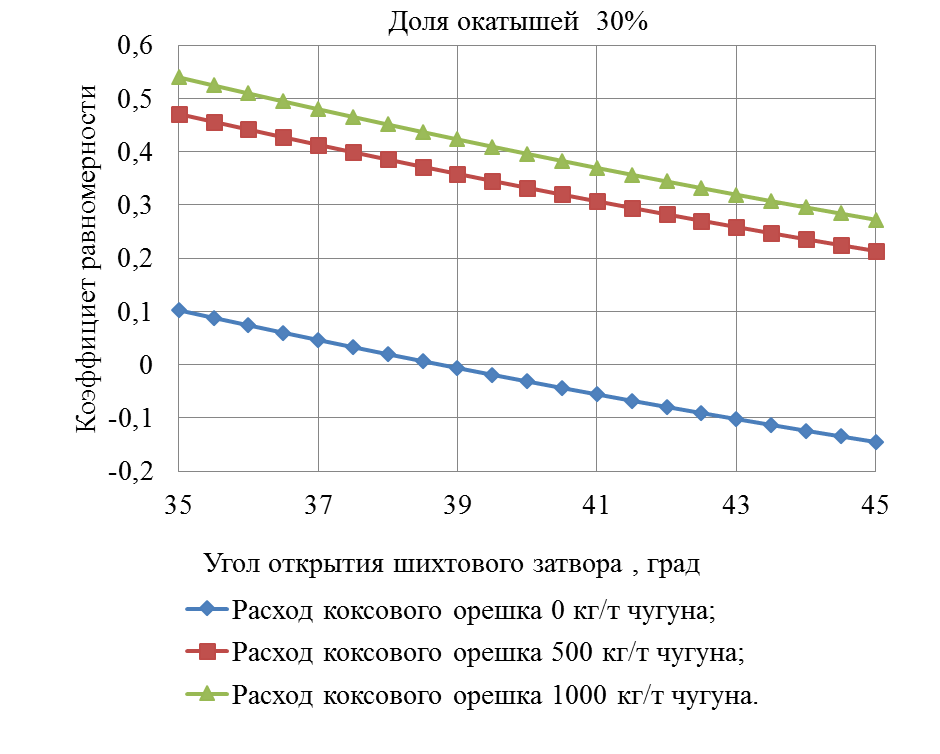
Рисунок 6 – Зависимость коэффициента равномерности от угла открытия шихтового затвора
На рисунке 6 зависимости коэффициента равномерности от угла открытия шихтового затвора и расходе коксового орешка при доле окатышей от железорудной части шихты 30% является криволинейной убывающей.
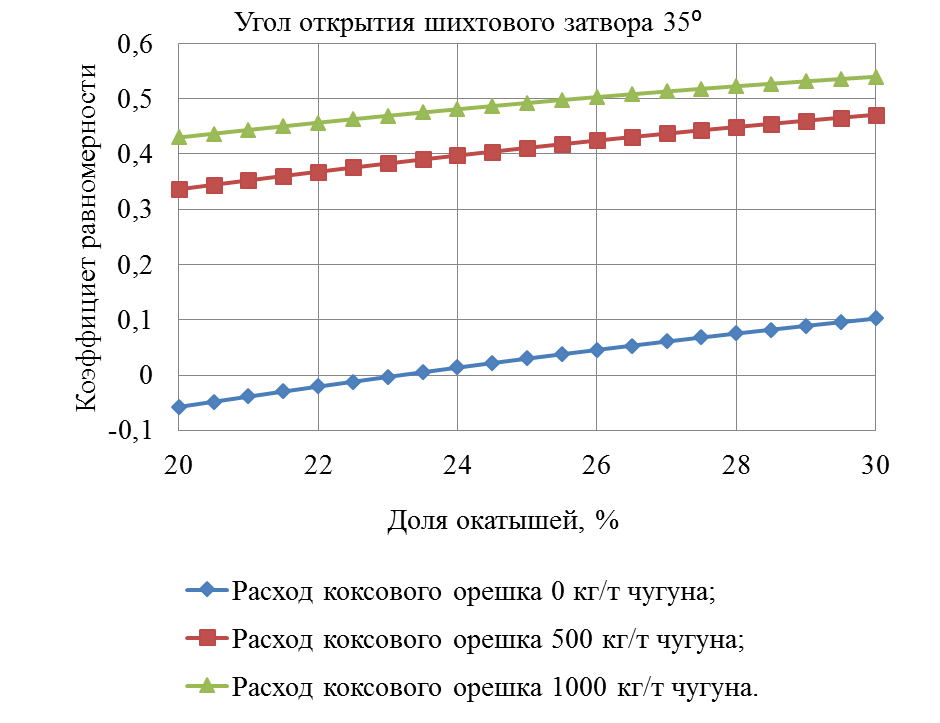
Рисунок 7 – Зависимость коэффициента равномерности от долей окатышей
На рисунке 7 зависимости коэффициента равномерности от доли окатышей и расходе коксового орешка при угле открытия шихтового затвора 35 ̊является криволинейной возрастающей.
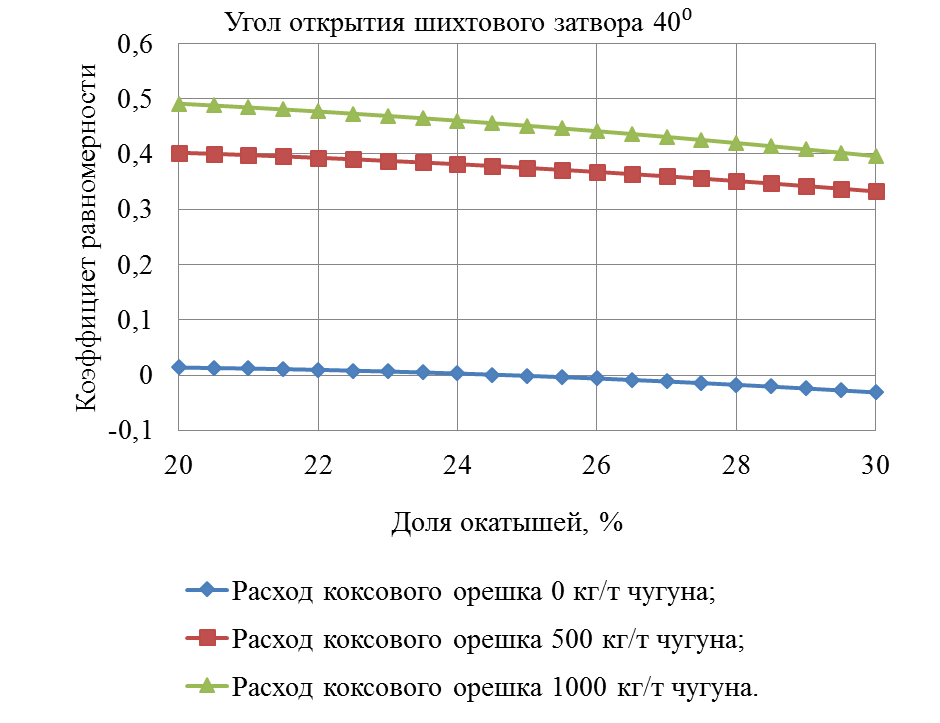
Рисунок 8 – Зависимость коэффициента равномерности от долей окатышей
На рисунке 8 зависимости коэффициента равномерности от доли окатышей и расходе коксового орешка при угле открытия шихтового затвора 40 ̊является криволинейной убывающей.
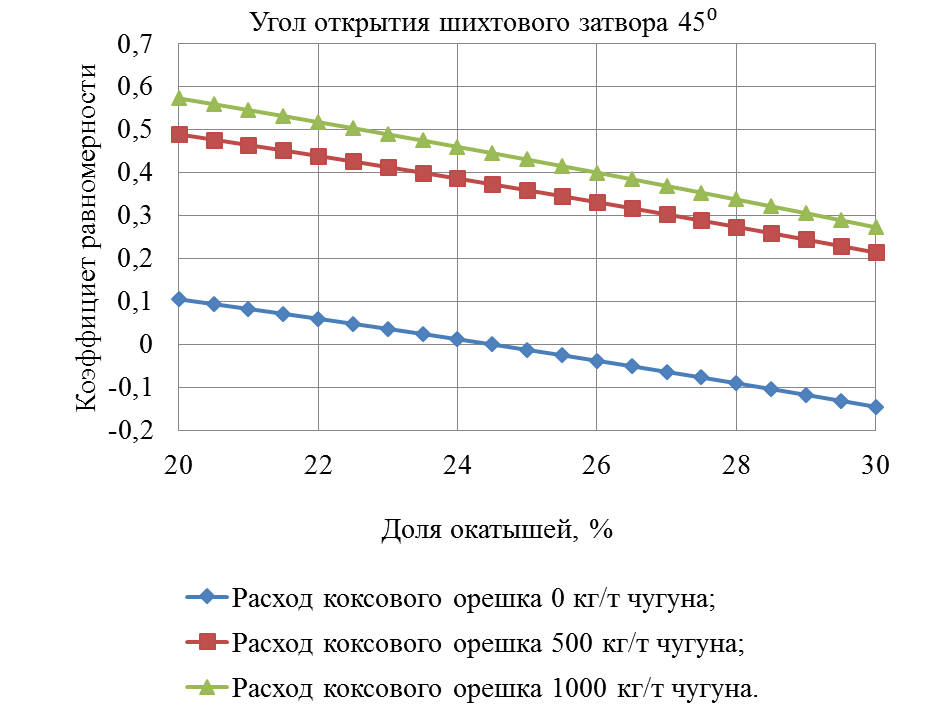
Рисунок 9 – Зависимость коэффициента равномерности от долей окатышей
На рисунке 9 зависимости коэффициента равномерности от доли окатышей и расходе коксового орешка при угле открытия шихтового затвора 45 ̊является криволинейной убывающей.
Таким образом, проанализировав зависимости, наиболее выгодным режимом загрузки материалов является: расход коксового орешка 900 кг/т чугуна, доля окатышей от железорудной части шихты 20%, угол открытия шихтового затвора 45 ̊.
Заключение
В данной работе проводился анализ влияния различных факторов на коэффициент равномерности поступления шихтовых материалов из шихтового бункера БЗУ в колошниковое пространство доменной печи, используя планированный эксперимент. При расходе коксового орешка 900 кг/т чугуна, доле окатышей от железорудной части шихты 20%, угле открытия шихтового затвора 45 ̊обеспечивало наиболее высокую величину коэффициента распределения равную 0,57975.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Спирин Н.А., Лавров В.В. Методы планирования и обработки результатов инженерного эксперимента: учебное пособие. – Екатеринбург: ГОУ ВПО “УГТУ – УПИ”, 2004. – 257 с.
2. Ковшов В.Н. Постановка инженерного эксперимента. Киев – Донецк: Высшая школа. Головное издательство, 1982. 120с.
3. Дружков В.Г., Заводяный А.В. Совершенствование технологии агломерации бурых железняков Орско – Халиловского рудного района. Магнитогорск: ГОУ ВПО “МГТУ им. Г.И. Носова”, 2010. 156 с.
4. Куприенко Н.В. Статистика. Методы анализа распределений. Выборочное наблюдение. 3-е изд.: СПб.: Издательство Политенического университета, 2009. 138 с.
5. Оншин Н.В. Основы теории планирования инженерного эксперимента. Магнитогорск. 2009. – 145 с.
6. Пригода В.П. Введение в теорию эксперимента: учебное пособие. – Магнитогорск: ГОУ ВПО “МГТУ им. Носова”, 2005. – 130 с.
ПРИЛОЖЕНИЕ 1
Дата добавления: 2019-11-16; просмотров: 422; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
