Проверка однородности ряда дисперсий
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ «МАГНИТОГОРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ ИМ. Г.И. НОСОВА»
Институт Металлургии, машиностроения и материалообработки
Кафедра металлургии и химических технологий
КУРСОВАЯ РАБОТА
по дисциплине: Планирование эксперимента»
На тему: «Анализ факторов, влияющих на равномерность состава шихты на колошнике доменной печи»
Исполнитель: Рыскужин А.И., студент 3 курса, группа ММб-16-1
Руководитель: зав. каф. МиХТ, канд.техн. наук Харченко А.С.
Работа допущена к защите «____» ___________ 2019 г. ______________
(подпись)
Работа защищена «____» _____________ 2019 г. с оценкой__________________
(подпись)
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ
«МАГНИТОГОРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Г.И. НОСОВА»
Институт металлургии, машиностроения и материалообработки
Кафедра металлургии и химических технологий
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
Тема: «Анализ факторов, влияющих на равномерность состава шихты на колошнике доменной печи»
Студенту: Рыскужину А.И., студент 3 курса, группа ММб-16-1
|
|
|
Вариант №1
Проанализировать влияние:
1. Рассчитать коэффициенты уравнения, оценить их значимость.
2. Проверить адекватность уравнения реальным данным.
3. Графически отобразить действие факторов на коэффициент равномерности поступления коксового орешка (промывочных материалов) из шихтового бункера БЗУ в колошниковое пространство печи.
В шихтовом бункере БЗУ материалы располагали следующим образом: агломерат вниз бункера, затем коксовый орешек, после чего окатыши.
Срок сдачи: «___» ________________________2019г.
Руководитель: _______________________/__________/
Задание получил:____________________/__________/
Исходные данные для варианта 1
Таблица 1
| Номер опыта | Факторы | Коэфф. равномерности | |||
| расход коксового орешка, кг/т чугуна | степень открытия шихтового затвора , градус | доля окатышей, % | Y1 | Y2 | |
| 1 | 0 | 40 | 25 | 0 | 0 |
| 2 | 0 | 45 | 20 | 0 | 0 |
| 3 | 0 | 45 | 30 | 0 | 0 |
| 4 | 0 | 50 | 25 | 0 | 0 |
| 5 | 500 | 40 | 20 | 0,19 | 0,31 |
| 6 | 500 | 40 | 30 | 0,21 | 0,41 |
| 7 | 500 | 50 | 20 | -0,2 | -0,1 |
| 8 | 500 | 50 | 30 | -0,28 | -0,16 |
| 9 | 1000 | 40 | 25 | 0,01 | 0,26 |
| 10 | 1000 | 45 | 20 | 0,07 | 0,27 |
| 11 | 1000 | 45 | 30 | -0,01 | 0,13 |
| 12 | 1000 | 50 | 25 | -0,02 | -0,16 |
| 13 | 500 | 45 | 25 | 0,34 | 0,42 |
Руководитель: __________________/ Харченко А.С.
|
|
|
Задание получил:_______________ / Рыскужин А.И.
СОДЕРЖАНИЕ
Введение. 8
1 Планирование эксперимента. 8
2 Проверка однородности ряда дисперсий.. 13
3 Расчет математической модели равномерности выхода исследуемого материала из шихтового бункера БЗУ лоткового типа в колошниковое пространство доменной печи.. 16
4 Проверка адекватности математической модели.. 18
5 Анализ результатов. 20
Заключение. 29
БИБЛИОГРАФИЧЕСКИЙ СПИСОК.. 31
ПРИЛОЖЕНИЕ 1.. 32
ПРИЛОЖЕНИЕ 2.. 33
ПРИЛОЖЕНИЕ 3.. 34
Цель работы: Изучить влияние различных факторов на коэффициент равномерности поступления коксового орешка, железной Михайловской и марганцевой руд из шихтового бункера БЗУ в колошниковое пространство доменной печи.
Исходные данные для варианта 1
Таблица 1
| Номер опыта | Факторы | Коэфф. равномерности | |||||
| расход коксового орешка, кг/т чугуна | степень открытия шихтового затвора , градус | доля окатышей, % | Y1 | Y2 | |||
| 1 | 0 | 40 | 25 | 0 | 0 | ||
| 2 | 0 | 45 | 20 | 0 | 0 | ||
| 3 | 0 | 45 | 30 | 0 | 0 | ||
| 4 | 0 | 50 | 25 | 0 | 0 | ||
| 5 | 500 | 40 | 20 | 0,19 | 0,31 | ||
| 6 | 500 | 40 | 30 | 0,21 | 0,41 | ||
| 7 | 500 | 50 | 20 | -0,2 | -0,1 | ||
| 8 | 500 | 50 | 30 | -0,28 | -0,16 | ||
| 9 | 1000 | 40 | 25 | 0,01 | 0,26 | ||
| 10 | 1000 | 45 | 20 | 0,07 | 0,27 | ||
| 11 | 1000 | 45
| 30 | -0,01 | 0,13 | ||
| 12 | 1000 | 50 | 25 | -0,02 | -0,16 | ||
| 13 | 500 | 45 | 25 | 0,34 | 0,42 | ||
Введение
Обеспечение равномерности состава шихты по окружности колошника доменной печи, является одним из решающих условий, обеспечивающей ровный и устойчивый ход печи. БЗУ лоткового типа не обеспечивает равномерного окружного распределения шихтовых материалов, что приводит к снижению производительности печи и увеличению удельного расхода кокса. Для снижения экономичности доменной плавки на печах, оборудованных БЗУ лоткового типа необходимо изучить факторы, влияющие на равномерность поступления шихтовых материалов из бункера БЗУ в колошниковое пространство печи и выявить их рациональный режим загрузки в печь.
Планирование эксперимента
Основными материалами шихты доменной печи являются кокс, агломерат и окатыши. В состав железорудной части шихты вводят различные добавки (коксовый орешек – для экономичности доменной плавки, железную Михайловскую и марганцевую руды – для очищения горна печи от мелочи и “спели” кокса, кварцит – для придания шлаку нужной основности). Расход добавок не превышает 13 % от содержимого одного скипа, вследствие чего происходит неравномерное их распределение по окружности колошника.
|
|
|
Для решения задачи по выявлению рационального режима загрузки шихтовых материалов в доменную печь, используя планированный эксперимент, необходимо провести анализ влияния различных факторов на коэффициент равномерности поступления шихтовых материалов из шихтового бункера БЗУ в колошниковое пространство доменной печи.
Выбор влияющих факторов остаётся самым ответственным и, в то же время, слабо поддающимся формализации этапом. С одной стороны, необходимо включить в план эксперимента все наиболее значимые аргументы, с другой, желательно стремиться к сокращению числа входных факторов, так как большое их количество усложняет и саму модель и её анализ, увеличивает количество опытов. Наиболее радикальные рекомендации по этому этапу сводятся к упованию на талант и опыт экспериментатора.
На равномерность поступления шихтовых материалов из шихтового бункера БЗУ в колошниковое пространство печи влияют следующие факторы:
1. расход исследуемых материалов;
2. угол открытия шихтового затвора;
3. месторасположение шихтовых материалов в бункере БЗУ.
Полный факторный план требует проведения числа опытов N [1]:
N = 2n; (1.1)
N = 3n; (1.2)
где:
2 и 3 – количество уровней комбинации факторов;
n – число факторов.
При количестве факторов равном 3 и варьировании их на трех уровнях число опытов составит 27. Для уменьшения общего количества опытов можно воспользоваться методом Бокса – Бенкена [2, 3]. Их количество снизится до 13 наблюдений (таблица 1.1).
Таблица 1.1
| № опыта | Факторы | Эффект взаимодействия | Квадрат фактора | Y1 | Y2 |
Yср | |||||||
| X1 | X2 | X3 | X1X2 | X2X3 | X1X3 | X12 | X22 | X32 |
| ||||
| 1 | -1 | -1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | |
| 2 | -1 | 0 | -1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | |
| 3 | -1 | 0 | 1 | 0 | 0 | -1 | 1 | 0 | 1 | 0 | 0 | 0 | |
| 4 | -1 | 1 | 0 | -1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | |
| 5 | 0 | -1 | -1 | 0 | 1 | 0 | 0 | 1 | 1 | 0,31 | 0,45 | 0,38 | |
| 6 | 0 | -1 | 1 | 0 | -1 | 0 | 0 | 1 | 1 | 0,42 | 0,52 | 0,47 | |
| 7 | 0 | 1 | -1 | 0 | -1 | 0 | 0 | 1 | 1 | 0,45 | 0,53 | 0,49 | |
| 8 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0,13 | 0,21 | 0,17 | |
| 9 | 1 | -1 | 0 | -1 | 0 | 0 | 1 | 1 | 0 | 0,43 | 0,53 | 0,48 | |
| 10 | 1 | 0 | -1 | 0 | 0 | -1 | 1 | 0 | 1 | 0,41 | 0,51 | 0,46 | |
| 11 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0,36 | 0,46 | 0,41 | |
| 12 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0,42 | 0,5 | 0,46 | |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0,36 | 0,39 | 0,375 | |
Матрица планирования экспериментов и эффекты взаимодействия в кодированном виде
В качестве выходного параметра, т.е. параметра оптимизации, используется коэффициент равномерности поступления исследуемого материала из шихтового бункера:
, (1.3)
где:
σi – среднеквадратическое отклонение по массе i-тых порций исследуемого материала, поступающих из шихтового бункера;
Мср – среднее значение поступающих из бункера порций исследуемого материала, по массе.
Выражение 
представляет собой коэффициент вариации [4].
Для математического описания выходного параметра от указанных факторов можно выбрать полином второй степени.
, (1.4)
где:
Xl,Xj – факторы, влияния которых на параметр оптимизации
исследуются;
B0 – постоянная составляющая;
Вj – линейная составляющая;
Blj – составляющая, учитывающая взаимодействие
факторов;
Bjj – квадратичная составляющая
Если эксперименты проводятся на модели необходимо соблюдать критерии подобия (Фруда, Эйлера, Рейнольдса).
В случае проведения исследований на физической модели однотрактового компактного загрузочного устройства, изготовленного в масштабе 1:5 по отношению к линейным размерам БЗУ доменных печей № 4 и 6 ОАО “ММК” достаточно соблюсти равенство критерия Ньютона для реальной печи (NДП) и модели(NeM):
, (1.5)
где:
Мп – масса, поступающей шихты из бункера БЗУ, кг;
L – расстояние, на которое перемещаются материалы, м;
– время, за которое происходит перемещение на
расстояние L, с;
F – сила тяжести материала, H.
Поскольку шихта из бункера движется под действием силы тяжести, то
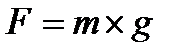; (1.6)
, (1.7)
где:
g – ускорение свободного падения g = 9,8 м/с2.
Формулы пересчета [2] массы шихты и времени ее перемещение на расстояние L с реальной печи на модель приведены в формулах 1.6 и 1.7 соответственно.
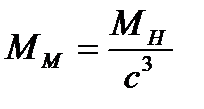, (1.8)
где:
– масса шихтовых материалов на модели;
– масса шихтовых материалов на доменной печи;
c – степень уменьшения модели.
, (1.9)
где:
– время ссыпания шихтовых материалов на модели;
– время ссыпания шихтовых материалов на доменной печи;
Для исключения систематических ошибок, при выполнении опытов по составленному в табл. 1.1 плану необходимо соблюдать рандомизацию.
Проверка однородности ряда дисперсий
Необходимо проверить однородность ряда дисперсий, чтобы убедится в неслучайности полученных значений, показателя равномерности поступления исследуемого материала из бункера БЗУ.
Матрица планирования включает 13 опытов, и дисперсия всего эксперимента определяется в результате усреднения дисперсий всех опытов.
Дисперсию каждого опыта состоящего из n повторных наблюдений необходимо определить по следующей формуле [5]:
, (2.1)
где:
– дисперсия u-го опыта, состоящего из n повторений.
n – число дублирующих опытов;
yui – результат i-го дубля u-го опыта;
– среднее арифметическое значение всех дублей опыта.
При равномерном дублировании всех опытов формула подсчета дисперсии эксперимента выглядит следующим образом [5]:
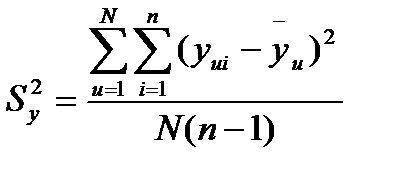, (2.2)
где:
Sy2 – дисперсия параметра оптимизации, или то же самое дисперсия воспроизводимости эксперимента S2воспр;
N – число опытов.
В условиях повторения каждого опыта два раза дисперсия воспроизводимости показателя равномерности выхода исследуемого материала из шихтового бункера БЗУ примет вид:
, (2.3)
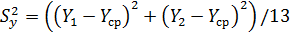
0,000754
| Номер опыта | Y1 | Y2 | Yср | Sy^2 |
| 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 |
| 5 | 0,31 | 0,45 | 0,38 | 0,000754 |
| 6 | 0,42 | 0,52 | 0,47 | 0,000385 |
| 7 | 0,45 | 0,53 | 0,49 | 0,000246 |
| 8 | 0,13 | 0,21 | 0,17 | 0,000246 |
| 9 | 0,43 | 0,53 | 0,48 | 0,000385 |
| 10 | 0,41 | 0,51 | 0,46 | 0,000385 |
| 11 | 0,36 | 0,46 | 0,41 | 0,000385 |
| 12 | 0,42 | 0,5 | 0,46 | 0,000246 |
| 13 | 0,36 | 0,39 | 0,375 | 3,46E-05 |
Число степеней свободы в данном случае определяем по формуле 2.4.
f1 = N(n – 1)=13·(2 – 1) = 13, (2.4)
Перед дальнейшим использованием полученной дисперсии необходимо проверить однородность ряда дисперсий. В случае равномерного дублирования опытов это выполняется по критерию Кохрена – G. Для этого из всех дисперсий находили наибольшую 
, которую делят на сумму всех дисперсий. Критерий Кохрена – это отношение максимальной дисперсии к сумме всех дисперсий:
, (2.5)
Ряд считали однородным, если выполняется условие [5]:
, (2.6)
где: Gp,N,f – табличное значение критерия Кохрена (приложение 1), при уровне значимости p, числу опытов N, и числа степеней свободы f=n-1.
Дата добавления: 2019-11-16; просмотров: 338; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!