Раздел 2. Кратные и криволинейные интегралы

Задание 2.1.

Пластина задана неравенствами в декартовой системе координат: – плотность материала, из которого изготовлена пластина. Найти массу пластины.

Теоретический минимум

_______________________________________________________________________

Масса плоской фигуры определяются по формуле: 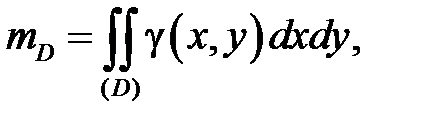 где  ‑ функция плотности, D – область интегрирования.

Двойной интеграл вычисляют сведением его к повторному интегралу:  Пределы интегрирования внешнего интеграла – всегда числа. Неравенство  задает вертикальную полосу, в которой располагается фигура D. Графики функций  ‑ это границы фигуры D соответственно слева и справа.

В первую очередь вычисляется внутренний интеграл, при этом интегрирование идет по переменной y, а x считается константой:

Результаты вычисления подставляют в первый интеграл, зависящий теперь

только от переменной :  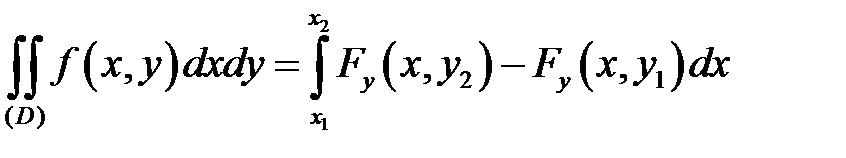и вычисляют полученный определенный интеграл.

Замечание 1: иногда удобно менять пределы интегрирования, тогда внутреннее интегрирование идет по переменной х, и двойной интеграл сведется к определенному интегралу от переменной у:

Замечание 2: если область интегрирования D представляет собой круг или его часть, то при вычислении интеграла рационально перейти от декартовой системы координат к полярной:

Для этого перехода уравнение границы области записывают в полярной системе координат и производят замену:

Замечание 3: если область интегрирования состоит из нескольких частей, то двойной интеграл представляют суммой интегралов по каждой из них.

_________________________________________________________

Решение:

Построим область интегрирования (D):

Рис. 1 К задаче 2.1.

Так как областью интегрирования является частью круга, то при вычислении двойного интеграла используем формулы перехода к полярным координатам:  при этом .

Уравнения линий, ограничивающих фигуру (D) в полярной системе координат имеют вид:

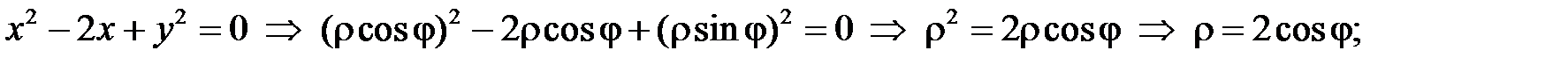
 Тогда (D):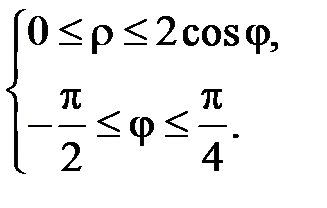

Вычисляем массу пластины:

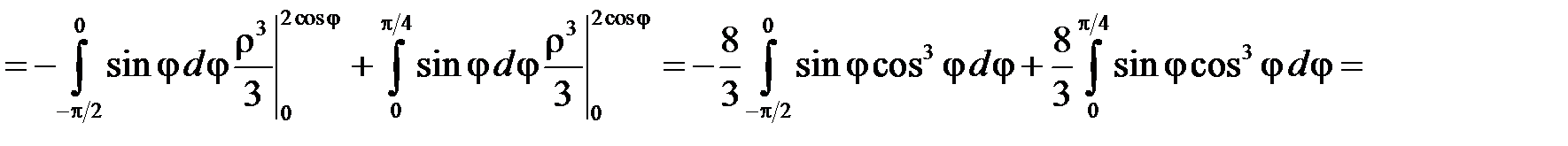
Ответ. Масса пластины равна

Задание 2.2.

C помощью тройного интеграла вычислить объем тела, ограниченного поверхностями: . Сделать чертежи данного тела и его проекции на координатную плоскость Oxy.

Теоретический минимум

_______________________________________________________________________

Объем тела вычисляется через тройной интеграл по замкнутой области от функции, равной единице: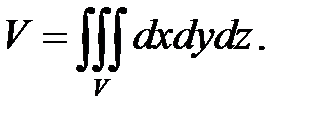  

Тройной интеграл вычисляют сведением его к повторному интегралу:

где  ‑ проекция тела V на плоскость Oхy.

При вычислении объема тела

_________________________________________________________________________________

 

Решение:

Построим область интегрирования, ее границы: координатные плоскости Oхy (уравнение z = 0) и Oх z (уравнение y = 0), плоскость у = 3-х, проходящая через точки (3, 0, 0) и (0, 3, 0) параллельно оси Oz, параболический цилиндр с направляющей z = 1 -x² и образующими, параллельными осиO у.

 

Рис. 2 К задаче 2.2.

Область (V) в направлении оси Oz ограничена снизу плоскостью z = 0, а сверху поверхностью z = 1 - x². Проекция области (V) на плоскость Oxy – трапеция ABС D. Стороны АВ и С D образованы пересечением параболического цилиндра с плоскостью z = 0, сторона ВС образована пересечением плоскости у = 3 - х с плоскостью z = 0, сторона А D образована пересечением координатных плоскостей Oхy и Oх z.

Тогда объем равен:

Последовательно вычисляем интегралы, начиная с внутреннего, причем при интегрировании по z переменные x и y фиксированы, а при интегрировании по y фиксирована переменная x.

Ответ. Объем V = 4.

Раздел 3. Теория поля

Задание 3.1.

Даны скалярное поле  точка  и вектор  Найти: а) скорость изменения скалярного поля U в точке А по направлению вектора 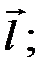 б) наибольшую скорость возрастания U в точке А.

Теоретический минимум

_______________________________________________________________________

Скалярное поле – это область пространства, на которой определена скалярная (числовая) функция 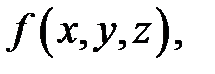 называемая функцией поля. Примеры скалярного поля: поле температур, поле давлений и т.п.

Поверхность  где функция поля принимает одинаковые значения, называется поверхностью уровня (в двумерном пространстве уравнение  задает линию уровня).

Вектор из частных производных функции поля называют градиентом поля  ‑ оператор Гамильтона (читается, как «набла»).

Градиент поля направлен в направлении, перпендикулярном поверхности уровня.

Для характеристики скорости изменения поля  по направлению вектора  вычисляют производную скалярного поля по направлению этого вектора, обозначаемую

Производная по направлению вычисляется по формуле:

 где

Поле  в точке М возрастает тогда и только тогда, когда  При этом наибольшая скорость возрастания поля соответствует направлению градиента  и равна

Поле  в точке М убывает тогда и только тогда, когда  При этом наибольшая скорость убывания поля соответствует направлению противоположном вектору градиента  и равна

_________________________________________________________________________________

 

Решение:

а) скорость изменения скалярного поля U в точке А по направлению

Вычисляем частные производные для функции U:

Следовательно,

Находим единичный вектор направления

Тогда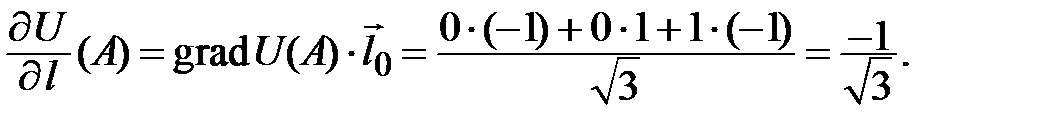

б) наибольшая скорость возрастания Uв точке А равна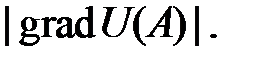

Находим длину градиента:

Ответ. а)  б)

Задание 3.2

Доказать, что векторное поле  потенциально, найти его потенциал. Выяснить, является ли поле 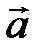 соленоидальным.

Теоретический минимум

______________________________________________________________________________

 

Векторное поле – область пространства, в каждой точке которой задан вектор  Примеры векторных полей: силовое поле, поле скоростей и т.п.

Важнейшими характеристиками векторного поля являются ротор и дивергенция.

1. Ротором векторного поля  называют вектор

Ротор, вычисленный в точке, характеризует вращательную способность векторного поля в этой точке.

Векторное поле называют потенциальным, если оно является полем градиента  некоторой скалярной функции U. Функцию  называют потенциалом поля.

Односвязное поле потенциально тогда и только тогда, когда его ротор равен нулю.

2. Дивергенцией векторного поля называют сумму частных производных координат вектор-функции  задающей векторное поле:

Дивергенция, вычисленная в точке, характеризует мощность источника (если ) или стока (если 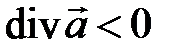) в этой точке.

Если  то векторное поле называют соленоидальным.

_____________________________________________________________________________________

Решение:

Поле является потенциальным, если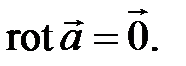

Вычисляем ротор :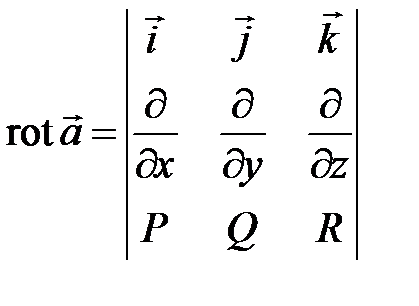

Значит, поле  потенциально и его потенциал U удовлетворяет условию  или в координатной форме: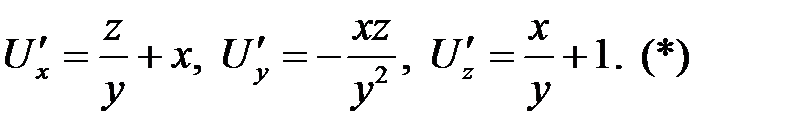

Найдем потенциал U.

1 способ. Проинтегрируем первое из этих равенств по x:

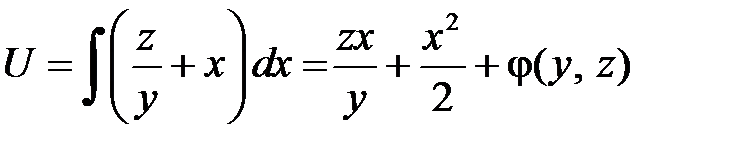
и подставим получившуюся функцию U(x, y, z)во второе равенство (*):  отсю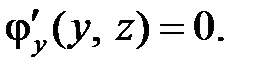да  Тогда  и Теперь подставим функцию U в третье равенство (*): Следовательно,  где С- константа. Поэтому

2 способ. Найдем потенциал по формуле

где в качестве начальной точки М₀(х₀, y₀, z₀) выберем точку с координатами (0, 1, 0). Получим

Замечание. При решении контрольной работы достаточно использовать только один способ для определения потенциала.

Поле является соленоидальным, если  Вычисляем дивергенцию:

.

Следовательно, поле  не является соленоидальным.

Ответ. Поле  потенциально, но не является соленоидальным; потенциал

Задание 3.3

Даны векторное поле  поверхность S:  и плоскость P: z = -3.Найти: а) поток поля 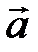 через внешнюю сторону замкнутой поверхности s, образованной поверхностью  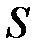и плоскостью Р; б) поток поля  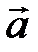через внешнюю сторону части поверхности  отсекаемой плоскостью Р; в) циркуляцию поля 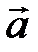 вдоль контура, образованного пересечением поверхности  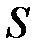и плоскости Р (направление обхода контура − положительное).

Решение:

Теоретический минимум

_______________________________________________________________________________________

Поток векторного поля  через ориентированную поверхность  с единичным вектором нормали - это поверхностный интеграл первого рода от скалярного произведения  по поверхности :

.

В формуле присутствуют следующие элементы:

1.  - функции от .

2.  - единичный вектор нормали к поверхности  способ его вычисления:

3. 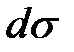 - элемент площади поверхности: способ его вычисления при проецировании поверхности s на плоскость Оху :

Тогда

Если поверхность s ‑ замкнутая, то удобно вычислять поток поля по теореме Остроградского-Гаусса: поток поля через замкнутую поверхность равен тройному интегралу от дивергенции поля по замкнутому объему:

___________________________________________________________

а) поток через замкнутую поверхность вычисляем по формуле Остроградского-Гаусса:

Тело V снизу ограничено плоскостью Р, сверху - параболоидом S.

Рис. 3 к задаче 3.3.

При вычислении интеграла перейдем к цилиндрическим координатам:

б) 1 способ.

По определению поток вектора  через поверхность σ равен  где 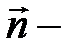нормаль поверхности σ. Если поверхность σ определятся уравнением F(x, y, z) = 0, то

Находим нормаль поверхности σ = S: Поток направлен во внешнюю сторону, поэтому (см.рис.) образует острый угол с осью Oz (третья координата вектора положительна). Тогда и интеграл равен

Получили поверхностный интеграл 2го рода. Сведем его к двойному интегралу. Из уравнения поверхности находим: 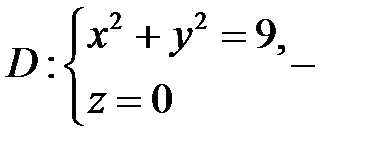проекция σ на плоскость Оху.

Получим

2 способ. Найдем поток  через поверхность параболоида как разность между потоком  через полную поверхность и потоком  через плоскость основания.

. Поверхность σ - часть плоскости Р, вырезаемая поверхностью 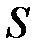. Нормаль поверхности: .

По формуле Остроградского поток через замкнутую поверхность направлен во внешнюю сторону, т.к. σ – нижнее основание замкнутой поверхности, то поток противоположно направлен оси Oz. Поэтому

где

Интеграл  определяет площадь круга с радиусом R = 3.

Тогда

Находим поток через поверхность параболоида:

в) Поверхность 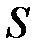 и плоскость Р пересекаются по окружности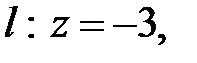

Циркуляция вектора  вдоль кривой (l) вычисляется по формуле:

В нашем случае 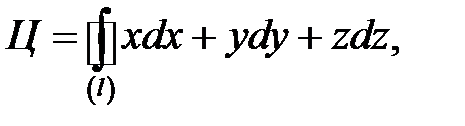 получили криволинейный интеграл 2го рода. Сведем этот интеграл к определенному интегралу с помощью параметрического задания окружности:  где 0 £ t £ 2p.

Вычисляем циркуляцию:

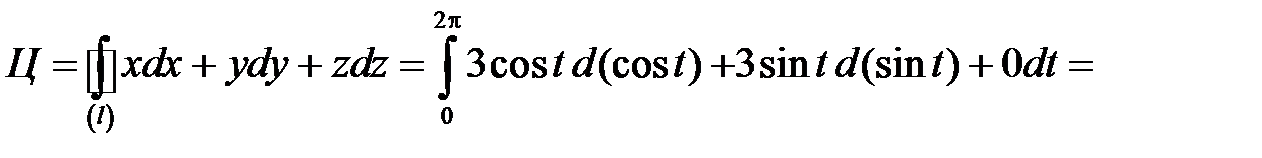
Замечание. При вычислении криволинейного интеграла необходимо учитывать направление обхода контура. По условию: направление положительное, т.е. против часовой стрелки, поэтому t изменяется от 0 до 2p.

Ответ. а)  б)  в)

Контрольные задания

Вариант 1

---

Дата добавления: 2019-09-13; просмотров: 209; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!