Примеры построения эпюры продольных сил
Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплен в стене (закрепление «заделка») (рис. 20.2а).
Делим брус на участки нагружения.
Участком нагружения считают часть бруса между внешними силами.
Тема 2.2. Растяжение и сжатие 177
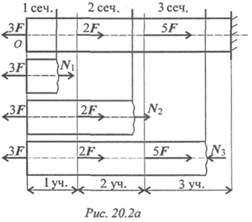На представленном рисунке 3 участка нагружения. Воспользуемся методом сечений и определим внутренние силовые факторы внутри каждого участка.
Расчет начинаем со свободного конца бруса, чтобы не определять величины реакций в опорах.
Участок 1: ∑ Fz = 0; -3F + N 1 = 0; N 1 = 3F. Продольная сила положительна, участок 1 растянут.
Участок 2: ∑ Fz = 0; -3F + 2F + N 2 = 0; N 2 = F . Продольная сила положительна, участок 2 растянут.
Участок 3: ∑ Fz = 0; -3F + 2F + 5F - N3 = 0; N 3 = 4F . Продольная сила отрицательна, участок 3 сжат. Полученное значение N 3 равно реакции в заделке.
Под схемой бруса строим эпюру продольной силы (рис. 20.26).
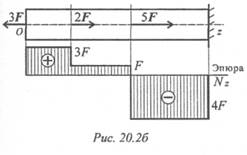Эпюрой продольной силы называется график распределения продольной силы вдоль оси бруса.
Ось эпюры параллельна продольной оси.
Нулевая линия проводится тонкой линией. Значения сил откладывают от оси, положительные — вверх, отрицательные — вниз. В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz .
Правило контроля: в месте приложения внешней силы на эпюре должен быть скачок на величину приложенной силы.
|
|
|
178 Лекция 20
На эпюре проставляются значения Nz . Величины продольных сил откладывают в заранее выбранном масштабе.
Эпюра по контуру обводится толстой линией и заштриховывается поперек оси.
Изучая деформации при растяжении и сжатии, обнаруживаем, что выполняются гипотеза плоских сечений и принцип смягчения граничных условий.
Гипотеза плоских сечений заключается в том, что поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформации остается плоским и перпендикулярным продольной оси.
Следовательно, продольные внутренние волокна удлиняются одинаково, а внутренние силы упругости распределены по сечению равномерно.
Принцип смягчения граничных условий гласит: в точках тела, удаленных от мест приложения нагрузки, модуль внутренних сил мало зависит от способа закрепления. Поэтому при решении задач не уточняют способ закрепления.
Напряжения при растяжении и сжатии
При растяжении и сжатии в сечении действует только нормальное напряжение.
Напряжения в поперечных сечениях могут рассматриваться как силы, приходящиеся на единицу площади.
|
|
|
Таким образом, направление и знак напряжения в сечении совпадают с направлением и знаком силы в сечении (рис. 20.3).
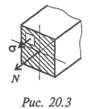Исходя из гипотезы плоских сечений, можно предположить, что напряжения при растяжении и сжатии в пределах каждого сечения не меняются. Поэтому напряжение можно рассчитать по формуле
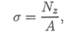где Nz — продольная cила в сечении; А — площадь поперечного сечения.
Величина напряжения прямо пропорциональна продольной силе и обратно пропорциональна площади поперечного сечения.
Нормальные напряжения действуют при растяжении от сечения (рис. 20.4а), а при сжатии к сечению (рис. 20.46).
Тема 2.2. Растяжение и сжатие 179
Размерность (единица измерения) напряжений — Н/м2 (Па), однако это слишком малая единица, и практически напряжения рассчитывают в Н/мм2 (МПа):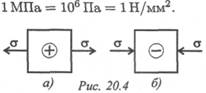 
При определении напряжений брус разбивают на участки нагружений, в пределах которых продольные силы не изменяются, и учитывают места изменений площади поперечных сечений.
Рассчитывают напряжения по сечениям, и расчет оформляют в виде эпюры нормальных напряжений.
|
|
|
Строится и оформляется такая эпюра так же, как и эпюра продольных сил.
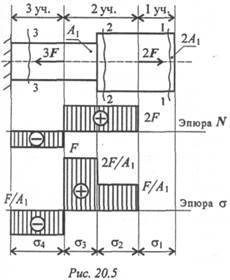
Рассмотрим брус, нагруженный внешними силами вдоль оси (рис. 20.5).
Обнаруживаем три участка нагружения и определяем величины продольных сил.
Участок 1: N 1 = 0. Внутренние продольные силы равны нулю.
Участок 2: N 2 = 2F . Продольная сила на участке положительна.
Участок 3: N3= 2F-3F = - F . Продольная сила на участке отрицательна.
Брус — ступенчатый. С учетом изменений величин площади поперечного сечения участков напряжений больше.
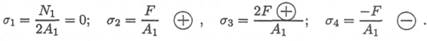
Строим эпюры продольных сил и нормальных напряжений. Масштабы эпюр могут быть разными и выбираются исходя из удобства построения.
180 Лекция 20
Примеры решения задач
Ступенчатый брус нагружен вдоль оси двумя силами. Брус защемлен с левой стороны (рис. 20.6). Пренебрегая весом бруса, построить эпюры продольных сил и нормальных напряжений.
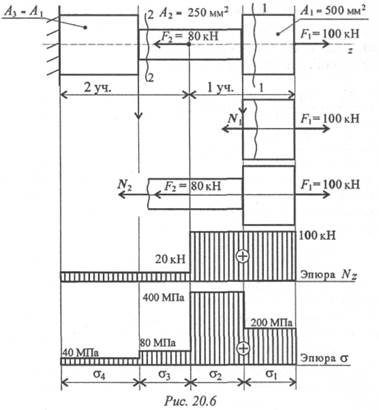
Решение
1. Определяем участки нагружения, их два.
2. Определяем продольную силу в сечениях 1 и 2.
3. Строим эпюру.
4. Рассчитываем величины нормальных напряжений и строим эпюру нормальных напряжений в собственном произвольном масштабе.
|
|
|
1. Определяем продольные силы.
Тема 2.2. Растяжение и сжатие 181
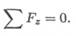
Сечение 1. – N1 + F1= 0; N1 = F1= 100 кН.
Сечение 2. -80 - N 2 + 100 = 0; N 2 = 100 - 80 = 20 кН.
В обоих сечениях продольные силы положительны.
Nz
2. Определяем нормальные напряжения σ = — .
A
Сопоставляя участки нагружения с границами изменения площади, видим, что образуется 4 участка напряжений. Нормальные напряжения в сечениях по участкам:
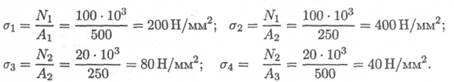
Откладываем значения напряжений вверх от оси, т. к. значения их положительные (растяжение). Масштаб эпюр продольной силы и нормальных напряжений выбирается отдельно в зависимости от порядка цифр и имеющегося на листе места.
Контрольные вопросы и задания
1. Какие внутренние силовые факторы возникают в сечении бруса при растяжении и сжатии?
2. Как распределяются по сечению силы упругости при растяжении и сжатии? (Использовать гипотезу плоских сечений.)
3. Какого характера напряжения возникают в поперечном сечении при растяжении и сжатии: нормальные или касательные?
4. Как распределены напряжения по сечению при растяжении и
сжатии?
5. Запишите формулу для расчета нормальных напряжений при
растяжении и сжатии.
6. Как назначаются знаки продольной силы и нормального напряжения?
7. Что показывает эпюра продольной силы?
8. Как изменится величина напряжения, если площадь поперечного сечения возрастет в 4 раза?
9. В каких единицах измеряется напряжение?
182 Лекция 21
ЛЕКЦИЯ 21
Дата добавления: 2019-09-13; просмотров: 2277; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!