Графический способ решения уравнений
Конспекты по математике
Тема: «Функции, их свойства и графики. Показательная, логарифмическая функции»
1. Показательная функция, ее свойства и графики.
Во многих отраслях науки и техники при изучении самых различных явлений и процессов обнаруживается одна общая функциональная зависимость между двумя переменными величинами, участвующими в процессе. Рассмотрим примеры.
Пример 1: С изменением высоты h над уровнем моря атмосферное давление p изменяется по закону  , где p0 - давление на уровне моря, а - постоянная ( const ).
, где p0 - давление на уровне моря, а - постоянная ( const ).
Пример 2: Рост древесины происходит по закону: 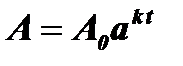 , где t - время, А0 - начальное количество древесины при t = 0, А - изменяющееся со временем количество древесины, а , k - постоянные ( const).
, где t - время, А0 - начальное количество древесины при t = 0, А - изменяющееся со временем количество древесины, а , k - постоянные ( const).
Пример 3: Размножение бактерий в какой-либо культуре происходит по закону:  , где t - время, у0 - начальное количество бактерий при t = 0 , у - изменяющееся со временем количество бактерий, а , k - постоянные ( const ).
, где t - время, у0 - начальное количество бактерий при t = 0 , у - изменяющееся со временем количество бактерий, а , k - постоянные ( const ).
Пример 4: Распад радия протекает по закону  , где t - время, х0 - начальное количество радия при t = 0, х - изменяющееся со временем количество радия, а , k - постоянные ( const).
, где t - время, х0 - начальное количество радия при t = 0, х - изменяющееся со временем количество радия, а , k - постоянные ( const).
В приведенных примерах мы имеем дело с процессами, носящими общее название «процессы органического роста». Если отвлечься от физического смысла переменных, участвующих в процессах органического роста и обозначить их х и у, то получим формулу  , где с , а , k - постоянные (const). Мы рассмотрим простейший случай:
, где с , а , k - постоянные (const). Мы рассмотрим простейший случай:  , с = k = 1 .
, с = k = 1 .
|
|
|
Определение: Функция вида  , где а > 0, а ¹ 1, называется показательной функцией.
, где а > 0, а ¹ 1, называется показательной функцией.
Замечание: При а = 1 функция является постоянной, так как 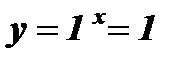 .
.
Свойства показательной функции  , а > 0 , а ¹ 1
, а > 0 , а ¹ 1
1) при 0 < а < 1 
 ;
;
2) при а > 1 а = 2  .
.
1. Областью определения функции являются все действительные числа, так как положительное число можно возвести в степень с любым действительным показателем: 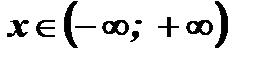 .
.
2. Множеством значений функции являются положительные числа, так как при возведении положительного числа в степень с любым действительным показателем получается положительное число:  .
.
Вывод: График показательной функции расположен в первой и второй координатных четвертях.
3. Функция не является ни четной ни нечетной:  ,
,  , f ( – х)¹ f (х), f ( – х)¹ – f ( х).
, f ( – х)¹ f (х), f ( – х)¹ – f ( х).
4. Функция является монотонной:
1) при 0 < а < 1 
 – убывающая функция;
– убывающая функция;
2) при а > 1 а = 2  – возрастающая функция.
– возрастающая функция.
Замечание:
1) При возведении в степень правильной дроби, чем больше показатель степени, тем меньше результат.
2) При возведении в степень числа, большего единицы, чем больше показатель степени, тем больше результат.
Функция является обратимой, так как она монотонна.
|
|
|
6. Нулей функции нет, так как уравнение у = 0 , то есть  корней не имеет.
корней не имеет.
7. Промежутки знакопостоянства: при 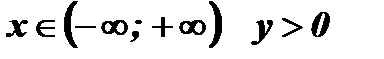 , так как
, так как
при 
при 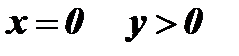
при 
8. Функция ограничена снизу, так как  при
при  .
.
9. Любая показательная функция проходит через точку (0; 1) , так как при
х = 0  .
.
Замечание:
1) При а > 1функция возрастает тем быстрее, чем больше а;
2) При 0 < а < 1 функция убывает тем быстрее, чем меньше а.
| х |
| у |
| - 3 |
| 1 |
| 2 |
| 3 |
| - 2 |
| - 1 |
| 0 |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |

|

|
0 < а < 1 

| х | - 3 | - 2 | - 1 | 0 | 1 | 2 | 3 |
| у | 8 | 4 | 2 | 1 | 
| 
| 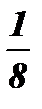
|
а > 1 а = 2 
| х | - 3 | - 2 | - 1 | 0 | 1 | 2 | 3 |
| у | 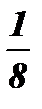
| 
| 
| 1 | 2 | 4 | 8 |
Упражнения:
1. Перечислите свойства функции и постройте ее график:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
2. Найдите множество значений функции:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
3. Сравните числа:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 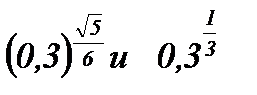 .
.
4. Вычислите:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
5. Укажите, какая из данных функций является возрастающей, какая – убывающей на множестве действительных чисел R:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
2. Показательные уравнения.
Определение: Показательными уравнениями называются уравнения, содержащие переменную в показателе степени.
|
|
|
1)  , а > 0 , а ¹ 1
, а > 0 , а ¹ 1
На основании определения степени с нулевым показателем решение уравнения  сводится к решению уравнения f( x)=0:
сводится к решению уравнения f( x)=0:
 .
.
Пример: Решить уравнение:  .
.
Решение:
 ; 1 = 20;
; 1 = 20; 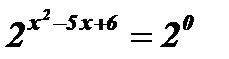 ;
;
 ;
;  ;
; 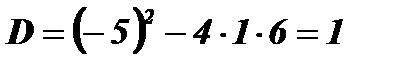 ;
;
 ;
; 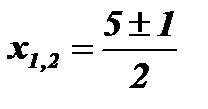 ; х1 = 2; х2 = 3.
; х1 = 2; х2 = 3.
Ответ: х1 = 2; х2 = 3.
Упражнения: Решить уравнение  :
:
1. а = 2 f ( x)= x2 - 40 x + 300;
2. а = 5 f ( x)= ( x2+ x - 2)(3 - x);
3. а = 3  ;
;
4. а = 2 f ( x)= x2 - 7 x + 12;
5. a = 0,5  .
.
2) 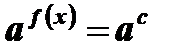 , а > 0 , а ¹ 1
, а > 0 , а ¹ 1
Левая и правая части уравнения  приведены к одному основанию. В этом случае корнями уравнения
приведены к одному основанию. В этом случае корнями уравнения  будут корни уравнения
будут корни уравнения  .
.
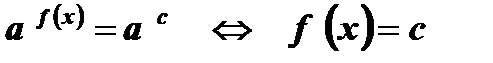 .
.
Пример: Решить уравнения:
1)  .
.
Решение:  ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;  ;
;
 ;
;  ; х1 =
; х1 =  ; х2 = 1.
; х2 = 1.
Ответ: х1 =  ; х2 = 1.
; х2 = 1.
2)  .
.
Решение:  ; 128 = 27;
; 128 = 27;
 ;
;  ; 6 х = 7; х =
; 6 х = 7; х = 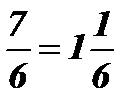 .
.
Ответ: х = 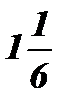 .
.
3)  .
.
Решение:
 ;
; 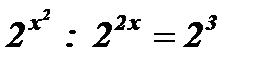 ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
 ;
;  ; х1 = - 1; х2 = 3.
; х1 = - 1; х2 = 3.
Ответ: х1 = - 1; х2 = 3.
Упражнения: Решить уравнения:
1.  ; ;
| 2.  ; ;
|
3.  ; ;
| 4.  ; ;
|
5.  ; ;
| 6. 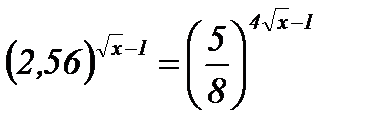 ; ;
|
7. 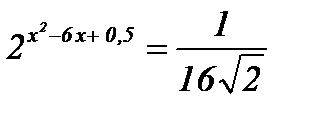 ; ;
| 8.  ; ;
|
9.  ; ;
| 10.  ; ;
|
11.  ; ;
| 12. 
|
3)  , а > 0 , а ¹ 1 , b > 0 , b ¹ 1 , а ¹ b
, а > 0 , а ¹ 1 , b > 0 , b ¹ 1 , а ¹ b
Уравнение решается делением обеих частей на  .
.
Пример: Решить уравнения:
1)  .
.
Решение: Разделим обе части уравнения на  .
.
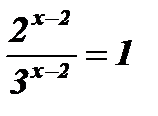 ;
;  ;
;  ; х - 2 = 0; х = 2.
; х - 2 = 0; х = 2.
Ответ: х = 2.
2)  .
.
Решение:  ;
;  ;
;  ;
;
Умножим обе части уравнения на  .
.
|
|
|
 ;
; 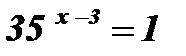 ;
;  ; х - 3 = 0; х = 3.
; х - 3 = 0; х = 3.
Ответ: х = 3.
Упражнения: Решить уравнения:
1)  ; ;
| 2) 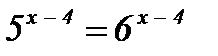 ; ;
|
3)  ; ;
| 4)  ; ;
|
5)  ; ;
| 6)  . .
|
4)  , а > 0 , а ¹ 1
, а > 0 , а ¹ 1
Особенностью уравнения является наличие одного и того же коэффициента перед х. Для решения этого уравнения выносят за скобки общий множитель 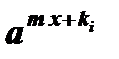 , где k i - наименьшее из чисел k0 , k1 , k2 , … , kп .
, где k i - наименьшее из чисел k0 , k1 , k2 , … , kп .
Пример:
1)  .
.
Решение:  ;
;  ;
;  ;
;  ;
;  ;
;  ; х = 4.
; х = 4.
Ответ: х = 4.
2)  .
.
Решение:
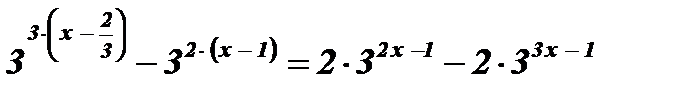 ;
;  ;
;
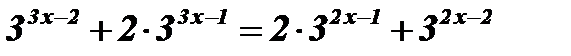 ;
;  ;
;
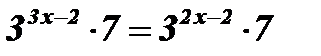 ;
;  ; 3х - 2 = 2х - 2; 3х - 2х = 2 - 2; х = 0.
; 3х - 2 = 2х - 2; 3х - 2х = 2 - 2; х = 0.
Ответ: х = 0.
3)  .
.
Решение:
 ;
;  ;
;
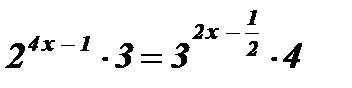 ;
;  ;
;  ;
;
 ;
; 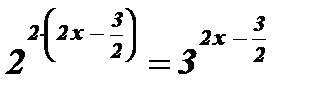 ;
;  ;
;
 ;
;  ;
;  ;
;  ;
;  .
.
Ответ:  .
.
Упражнения: Решить уравнения:
1)  ; ;
| 2)  ; ;
|
3)  ; ;
| 4)  ; ;
|
5) 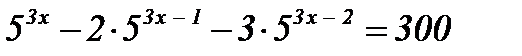 ; ;
| 6)  . .
|
5)  , а > 0 , а ¹ 1
, а > 0 , а ¹ 1
Уравнение  с помощью подстановки
с помощью подстановки  обращается в квадратное уравнение:
обращается в квадратное уравнение:  . Решив квадратное уравнение, найдем у1, у2 . После этого решение уравнения
. Решив квадратное уравнение, найдем у1, у2 . После этого решение уравнения  сводится к решениюдвух уравнений:
сводится к решениюдвух уравнений:  ,
,  .
.
Пример:
1)  .
.
Решение:  ;
; 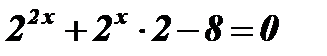 ;
;  ;
;
 ;
;  ;
;  ;
;
 ;
; 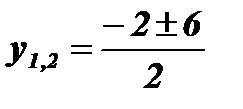 ; у1 = - 4; у2 = 2;
; у1 = - 4; у2 = 2;
 - уравнение корней не имеет, так как
- уравнение корней не имеет, так как  ;
;
 ; х = 1.
; х = 1.
Ответ: х = 1.
2)  .
.
Решение:
 ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
 ;
;  ; у1 = 1; у2 = 3;
; у1 = 1; у2 = 3;
 ; х2 - 1 = 0; х2 = 1; х1 = - 1; х2 = 1;
; х2 - 1 = 0; х2 = 1; х1 = - 1; х2 = 1;
 ; х2 - 1 = 1; х2 = 2; х3 =
; х2 - 1 = 1; х2 = 2; х3 =  ; х4 =
; х4 = 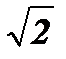 .
.
Ответ: х1 = - 1; х2 = 1; х3 =  ; х4 =
; х4 = 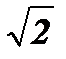 .
.
Упражнения: Решить уравнения:
1)  ; ;
| 2)  ; ;
|
3)  ; ;
| 4)  ; ;
|
5) 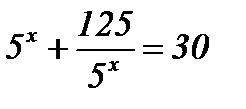 ; ;
| 6)  ; ;
|
7)  . .
|
6)  , а > 0 , а ¹ 1, b > 0 , b ¹ 1.
, а > 0 , а ¹ 1, b > 0 , b ¹ 1.
Отметим, что в выражении  показатели степеней в первом и третьем слагаемых вдвое больше показателей степеней во втором слагаемом. Такие выражения называются однородными 2-ого порядка. А уравнения вида
показатели степеней в первом и третьем слагаемых вдвое больше показателей степеней во втором слагаемом. Такие выражения называются однородными 2-ого порядка. А уравнения вида  называются однородными 2-ого порядка. Разделив уравнение на
называются однородными 2-ого порядка. Разделив уравнение на  , получим:
, получим: 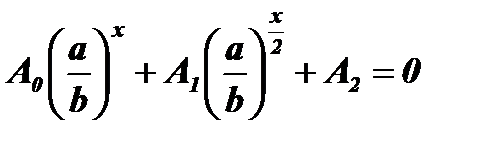 .
.
Уравнение 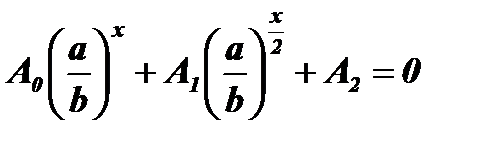 с помощью подстановки
с помощью подстановки  обращается в квадратное уравнение:
обращается в квадратное уравнение:  . Решив квадратное уравнение, найдем у1, у2 и, возвращаясь к первоначальной переменной, получим два уравнения
. Решив квадратное уравнение, найдем у1, у2 и, возвращаясь к первоначальной переменной, получим два уравнения  и
и  .
.
Пример:  .
.
Решение:  ;
; 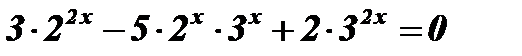 ;
;
Разделим обе части уравнения на  :
:
 ;
;  ;
;
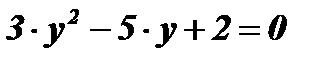 ;
;  ;
;  ;
;
 ;
;  ; у1 =
; у1 =  ; у2 = 1;
; у2 = 1;
 ; х1 = 1;
; х1 = 1;  ; х2 = 0.
; х2 = 0.
Ответ: х1 = 1; х2 = 0 .
Упражнения: Решить уравнения:
1)  ; ;
| 2)  ; ;
|
3)  ; ;
| 4)  . .
|
Графический способ решения уравнений
Уравнение  можно рассматривать как задачу об отыскании таких значений переменной х , при которых значения двух данных функций равны.
можно рассматривать как задачу об отыскании таких значений переменной х , при которых значения двух данных функций равны.
Рассмотрим уравнение вида  . Графический способ решения такого вида уравнений заключается в отыскании приближенных значений абсцисс точек пересечения графиков функций
. Графический способ решения такого вида уравнений заключается в отыскании приближенных значений абсцисс точек пересечения графиков функций  и
и  в одной и той же системе координат.
в одной и той же системе координат.
| х2 |
| х1 |
| х |
| у |
| - 3 |
| 1 |
| 2 |
| 3 |
| - 2 |
| - 1 |
| 0 |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |

|
| 9 |

|
 .
.
Решение:
у = х2
| х | - 3 | - 2 | - 1 | 0 | 1 | 2 | 3 |
| у | 9 | 4 | 1 | 0 | 1 | 4 | 9 |

| х | - 3 | - 2 | - 1 | 0 | 1 | 2 | 3 |
| у | 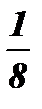
| 
| 
| 1 | 2 | 4 | 8 |
Ответ: х1 » - 0,7; х2 = 2.
Упражнения: Решите графически уравнения:
1)  ; ;
| 2)  ; ;
|
3)  ; ;
| 4) 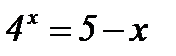 ; ;
|
5)  ; ;
| 6)  ; ;
|
7)  ; ;
| 8)  . .
|
3. Показательные неравенства.
Определение: Показательными неравенствами называются неравенства, содержащие переменную в показателе степени.
Решение простейших показательных неравенств основано на известном свойстве функции  : показательная функция возрастает при
: показательная функция возрастает при  и убывает при
и убывает при  .
.


Пример: Решить неравенства:
1. 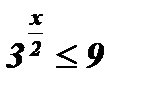 .
.
Решение: 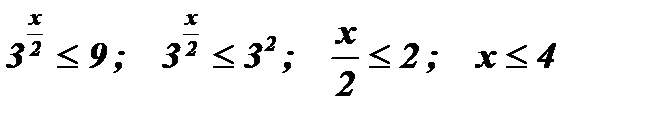 .
.
Ответ:  .
.
2. 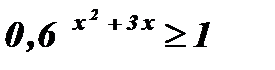 .
.
Решение:  ;
;
а = 1> 0 ветви параболы направлены вверх;
х 2 + 3х = 0;  ;
;
| х |
| + |
| + |
| - |
| - 3 |
| 0 |
Ответ: 
3. 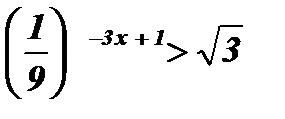 .
.
Решение:
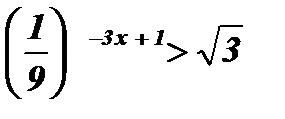 ;
;  ;
;  ;
; 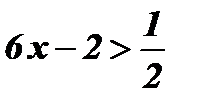 ;
;  ;
;
 ;
;  ;
;  .
.
Ответ: 
Упражнения: Решить неравенства:
1. 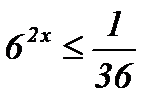 ; ;
| 2.  ; ;
|
3.  ; ;
| 4.  ; ;
|
5.  ; ;
| 6.  ; ;
|
7.  ; ;
| 8. 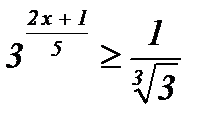 ; ;
|
9.  ; ;
| 10.  ; ;
|
13. 
|
4. Понятие логарифма. Основное логарифмическое тождество.
Необходимость возникновения нового понятия появилась из практической потребности при решении конкретных задач.
| х |
| у |
| - 3 |
| 1 |
| 2 |
| 3 |
| - 2 |
| - 1 |
| 0 |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
а с= b
2 с = 2 Þ с = 1;
2 с = 3 Þ с = 1,…;
2 с = 4 Þ с = 2;
2 с = 7 Þ с = 2,…;
2 с = 8 Þ с = 3;
Определение: Логарифмомчисла b по основанию а называется показатель степени с, в которую надо возвести данное основание а, чтобы получить число b.

Вывод:  .
.
 - основное логарифмическое тождество.
- основное логарифмическое тождество.
Замечание:
- Логарифмы чисел, вычисленные по одному и тому же основанию, образуют систему логарифмов.
- Систему логарифмов по основанию 10 называют системой десятичных логарифмов. Обозначение:
 .
. - Систему логарифмов по основанию е » 2,718281828459045 называют системой натуральных логарифмов. Обозначение:
 .
.
Пример:
1. Чему равен  ?
?
Решение: 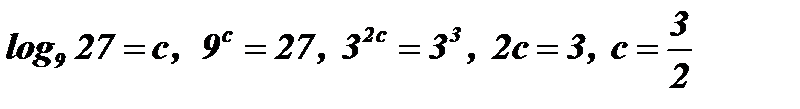 .
.
Ответ:  .
.
2. При каком основании  ?
?
Решение:  .
.
Ответ: 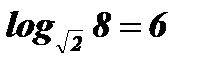 .
.
3. Найти число, логарифм которого при основании 64 равен  .
.
Решение:  .
.
Ответ:  .
.
Упражнения: Вычислить:  ;
;
1)  ; ;
| 2) 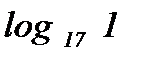 ; ;
| 3)  ; ;
|
4)  ; ;
| 5)  ; ;
| 6)  ; ;
|
7)  ; ;
| 8)  ; ;
| 9)  ; ;
|
10)  ; ;
| 11)  ; ;
| 12)  ; ;
|
13)  . .
|
5. Свойства логарифмов. Логарифмирование и потенцирование.
1)  , так как
, так как  .
.
2)  , так как
, так как  .
.
3) Логарифм произведения двух или нескольких положительных чисел равен сумме логарифмов сомножителей:
 .
.
4) Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя:  .
.
5) Логарифм степени положительного числа равен показателю степени, умноженному на логарифм основания:  .
.
6) Логарифм корня из положительного числа равен логарифму подкоренного выражения, деленному на показатель корня:
 .
.
Пример: Вычислить:
-
 ;
; -
 ;
; -
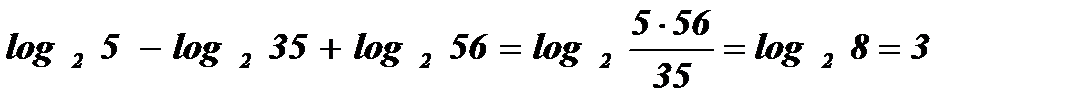 ;
; -

 ;
;
-
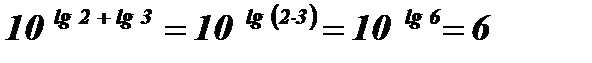 ;
; -
 .
.
Определение: Логарифмированием данного выражения называется представление логарифма этого выражения через логарифмы входящих в него элементов.
Замечание: Сумма и разность выражений не логарифмируются.
Пример:
1. Прологарифмировать данное выражение:
1)  .
.
Решение:  .
.
2)  .
.
Решение: 
3)  .
.
Решение:
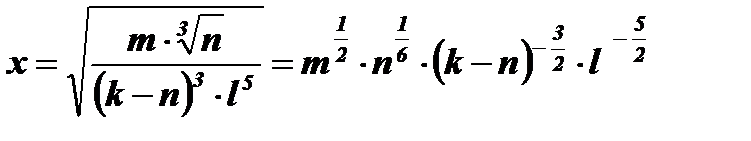 .
.
 .
.
2. Вычислить:  .
.
Решение:  .
.
Ответ:  .
.
Определение: Потенцированием называется нахождение выражения по его логарифму. Потенцирование – это действие,обратное логарифмированию.
Пример: Пропотенцировать :  .
.
Решение:
 ;
;
 .
.
Ответ:  .
.
Упражнения:
1. Вычислить:
1)  ; ;
| 2)  ; ;
|
3)  ; ;
| 4)  ; ;
|
5)  ; ;
| 6) 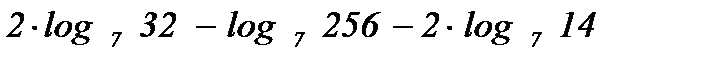 ; ;
|
7)  ; ;
| 8) 
|
- Прологарифмировать данное выражение:
1)  ; ;
| 2)  ; ;
|
3)  ; ;
| 4)  ; ;
|
5)  ; ;
| 6)  ; ;
|
7)  ; ;
| 8)  ; ;
|
9)  . .
|
- Пропотенцировать:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  .
.
- Найти х , если:
1)  ;
;
2)  ;
;
3)  .
.
6. Логарифмическая функция, ее свойства и графики.
Определение: Функция, обратная показательной функции, называется логарифмической.
 - показательная функция;
- показательная функция;
 Û
Û  ;
;
 - логарифмическая функция.
- логарифмическая функция.
- Область определения функции:
 , так как по определению
, так как по определению 
- Множество значений функции:
 , так как показатель степени может быть любым действительным числом.
, так как показатель степени может быть любым действительным числом.
Вывод: График логарифмической функции расположен в первой и четвертой координатных четвертях.
- Функция не является ни четной ни нечетной, так как её область определения не симметрична относительно начала координат.
- Функция является монотонной:
1) при 0 < а < 1 
 – убывающая функция;
– убывающая функция;
2) при а > 1 а = 2  – возрастающая функция.
– возрастающая функция.
- Функция является обратимой, так как она монотонна:
 - логарифмическая функция;
- логарифмическая функция;

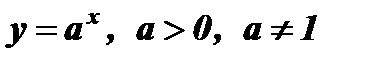 - показательная функция.
- показательная функция.
- у = 0;
 ; х = 1 - нуль функции.
; х = 1 - нуль функции. - Промежутки знакопостоянства:
1) при 0 < а < 1
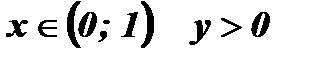 ;
;
 .
.
2) при а > 1
 ;
;
 .
.
- Функция является неограниченной сверху и снизу.
- Любая логарифмическая функция проходит через точку (1; 0) , так как при х = 1
 .
.
Замечание: Для построения графика логарифмической функции можно воспользоваться свойством графиков взаимно обратных функций: графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов, то есть относительно прямой у = х.
 (0 < а < 1)
(0 < а < 1)
| х | 8 | 4 | 2 | 1 | 
| 
| 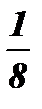
|
| у | - 3 | - 2 | - 1 | 0 | 1 | 2 | 3 |
| х |
| у |
| - 3 |
| 1 |
| 2 |
| 3 |
| - 2 |
| - 1 |
| 0 |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| - 1 |
| - 2 |
| - 3 |

|

|
| у = х |
 (а > 1)
(а > 1)
| х | 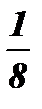
| 
| 
| 1 | 2 | 4 | 8 |
| у | - 3 | - 2 | - 1 | 0 | 1 | 2 | 3 |
| х |
| у |
| - 3 |
| 1 |
| 2 |
| 3 |
| - 2 |
| - 1 |
| 0 |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| - 1 |
| - 2 |
| - 3 |

|

|
| у = х |
Упражнения:
- Найти область определения выражения:
1)  ; ;
| 2)  ; ;
|
3)  ; ;
| 4)  ; ;
|
5)  ; ;
| 6)  ; ;
|
7)  ; ;
| 8)  . .
|
- Постройте график функции и перечислите ее основные свойства:
1)  ;
;
2)  ;
;
3)  ;
;
7. Логарифмические уравнения.
Определение: Уравнения, содержащие переменную только под знаком логарифма или в основании логарифма, называются логарифмическими.
Замечание: Простейшими логарифмическими уравнениями являются уравнения вида  и
и  .
.
1) Логарифмические уравнения, решаемые с помощью определения логарифма.



Пример: Решить уравнения:
1.  .
.
Решение:  Û
Û  Û
Û  Û
Û  .
.
Ответ:  .
.
2.  .
.
Решение:  Û
Û  Û
Û 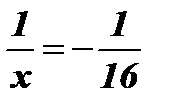 Û
Û  .
.
Ответ: х = - 16.
3. 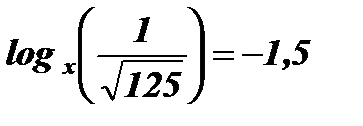 .
.
Решение:
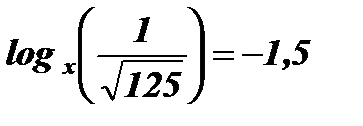 Û
Û  Û
Û 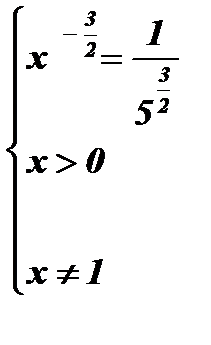 Û
Û
Û  Û
Û 
Ответ: х = 5.
4.  .
.
Решение:
 Û
Û  Û
Û  Û
Û  Û
Û
Û 
Ответ:  .
.
Упражнения: Решить уравнения:
1.  ; ;
| 2.  ; ;
|
3.  ; ;
| 4.  ; ;
|
5. 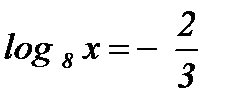 ; ;
| 6.  ; ;
|
7. 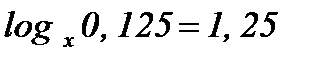 ; ;
| 8.  . .
|
2) Логарифмические уравнения, решаемые потенцированием.
Вывод: При решении логарифмического уравнения находят его область определения и проверяют корни на принадлежность области определения данного уравнения или делают проверку всех найденных корней подстановкой в исходное уравнение.
Пример: Решить уравнения:
1. 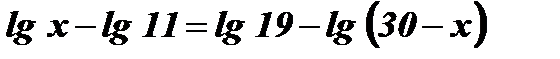 .
.
Решение:
Найдем область определения уравнения, используя определение логарифма:

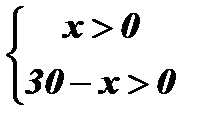 Û
Û  Û
Û  .
.
 Û
Û  Þ
Þ
Þ  Þ
Þ  Û
Û  ;
;
 ;
;
 ;
; 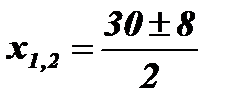 ; х1 =11; х2 = 19.
; х1 =11; х2 = 19.
Проверка:
Все корни принадлежат области определения уравнения.
 ;
; 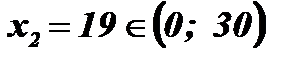 .
.
Ответ: х1 =11; х2 = 19.
2.  .
.
Решение:
Найдем область определения уравнения, используя определение логарифма:

 Û
Û  Û
Û  .
.
 Û
Û  Û
Û
Û  Þ
Þ  Û
Û  Û
Û
Û  Û
Û  .
.
Проверка:
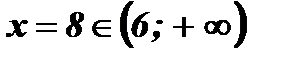 .
.
Ответ: х = 8.
3.  .
.
Решение: Найдем область определения уравнения, используя определение логарифма: 
 Û
Û 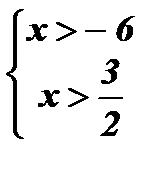 Û
Û  .
.
 Û
Û  Û
Û
Û  Û
Û  Þ
Þ
Þ  Û
Û  Û
Û
Û  Û
Û  Û
Û
Û 
 ;
;
 ;
;  ; х1 = 6; х2 = 14.
; х1 = 6; х2 = 14.
 Û
Û 
Проверка: Все корни принадлежат области определения уравнения.
 ;
;  ;
;
Ответ: х1 = 6; х2 = 14.
4.  .
.
Решение:
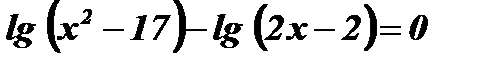 Û
Û  Þ
Þ 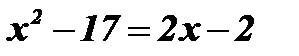 Û Û
Û Û 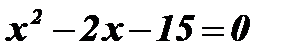 ;
; 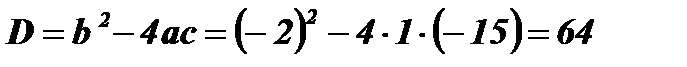 ;
;
 ;
;  ; х1 = - 3; х2 = 5.
; х1 = - 3; х2 = 5.
Проверка:
х1 = - 3;  ;
;
х1 = - 3 не является корнем данного уравнения, так как  не существует.
не существует.
х2 = 5;  .
.
Ответ: х =5.
Упражнения: Решить уравнения:
1.  ; 7.
; 7.  ;
;
2.  ; 8.
; 8. 
3.  ; 9.
; 9. 
4.  ; 10.
; 10. 
5. 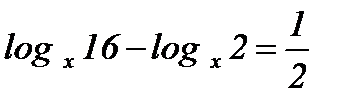 ; 11.
; 11. 
6.  ; 12.
; 12. 
3) Логарифмические уравнения степени выше первой относительно логарифма.
Замечание: При решении уравнений этого типа нужно обратить внимание на преобразования вида:
1.  ;
;
2. 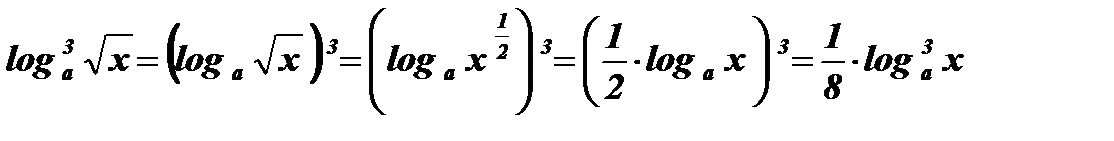 .
.
Пример: Решить уравнения:
-
 .
.
Решение:
 Û
Û  ;
;
Введем новую переменную  :
:  ;
;
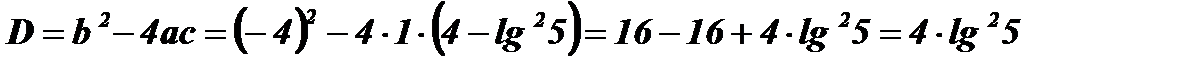 ;
;
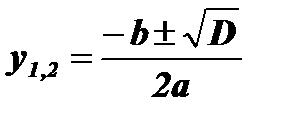 ;
;  ;
; 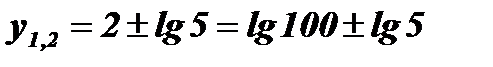 ;
;
 ;
;  ; х1 = 20.
; х1 = 20.
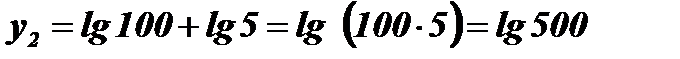 ;
;  ; х2 = 500.
; х2 = 500.
Проверка:
х1 = 20;

х2 = 500;

Ответ: х1 = 20; х2 = 500 .
-
 .
.
Решение:
Введем новую переменную: у = lgx .
 Û
Û  Û
Û
Û 
 Û
Û  Û
Û
Û  Û
Û  Û
Û 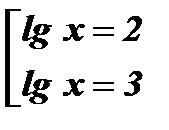 Û
Û 
 ;
;  ;
;
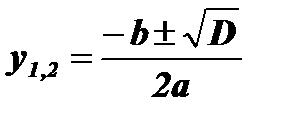 ;
;  ; у1 = 2; у2 = 3;
; у1 = 2; у2 = 3;
Ответ: х1 = 100; х2 = 1000.
Упражнения: Решить уравнения:
|
|
|
|
|
|
| 8.  ; ;
|
4) Уравнения, содержащие выражения вида 
При решении уравнений, содержащих переменную и в основании степени, и в показателе степени, используется метод логарифмирования. Если при этом в показателе степени содержится логарифм, то обе части уравнения надо логарифмировать по основанию этого логарифма.
При логарифмировании уравнения возможна потеря корней. Однако, если логарифмировать уравнение  , обе части которого положительны на всей области определения уравнения, то потери корней не произойдет. В этом случае говорят, что уравнения
, обе части которого положительны на всей области определения уравнения, то потери корней не произойдет. В этом случае говорят, что уравнения  и
и  равносильны на всей области определения данного уравнения.
равносильны на всей области определения данного уравнения.
Пример: Решить уравнения:
1.  .
.
Решение:
Найдем область определения уравнения, используя определение логарифма:
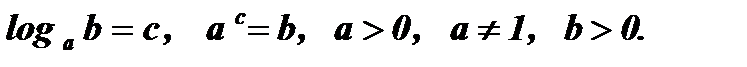
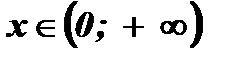 .
.
В области определения уравнения выражения, содержащиеся в обеих его частях, принимают только положительные значения. Следовательно, можно прологарифмировать обе части уравнения по основанию 10.
Таким образом, на области определения данного уравнения следующие уравнения равносильны:
 Û
Û  Û
Û  Û
Û  Û
Û  Û х1 = 0,01 или х2 =100.
Û х1 = 0,01 или х2 =100.
Проверка:
Все корни принадлежат области определения уравнения.
 ;
; 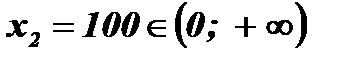
Ответ: х1 = 0,01; х2 =100.
2. 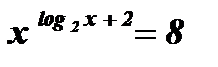 .
.
Решение:
Найдем область определения уравнения, используя определение логарифма:
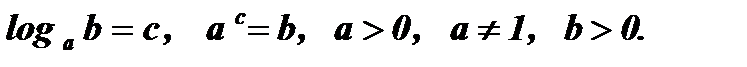
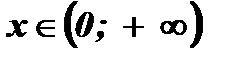 .
.
Дата добавления: 2019-09-13; просмотров: 290; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 ;
; ;
;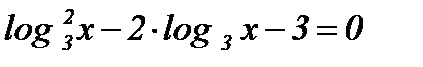 ;
; ;
; ;
; ;
;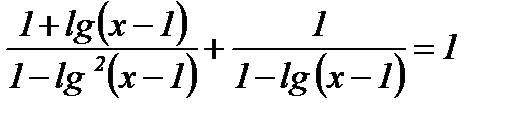 ;
;