Пример решения задачи с помощью МАИ
Коломенский институт (филиал)
федерального государственного бюджетного образовательного учреждения высшего образования
«МОСКОВСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра автоматизации производства и информационных
технологий
Романов П.С., Романова И.П.
Методические указания к практическому занятию
По дисциплине
ОСНОВЫ СИСТЕМ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА
Метод анализа иерархий
Коломна – 2017 г.
Содержание
| 1. | Введение .................................................................................................................... | 2 |
| 2. | Решение задач принятия решений на основе метода анализа иерархий....................... | 2 |
| 2.1. | Методика решения задач………………………………………………………………… | 2 |
| 2.2. | Пример решения задачи с помощью МАИ……………………………………..……… | 5 |
| 3. | Контрольные задания…………………………………………………………………..… | 11 |
| 4. | Структура отчета......................................................................................................... | 12 |
| 5. | Исходные данные………………………………………………………………………… | 12 |
| 6. | Литература................................................................................................................ | 20 |
Введение
Практическое занятие выполняется на основе теоретических положений искусственного интеллекта на ПК с использованием системы MatLab (MATLAB) или другого программного продукта (например, Microsoft Excel) и Microsoft WORD в среде Windows 9*/NT/2000/ХР. В результате изучения материала занятия обучаемые должны:
|
|
|
иметь представление: о типовых задачах, решаемых методом анализа иерархий;
знать: этапы решения задач на основе метода анализа иерархий; основные теоретические положения метода анализа иерархий; методику решения задач в условиях неопределенности на основе метода анализа иерархий;
уметь: применять метод анализа иерархий для решения задач принятия решений;
иметь навык: в решении задач принятия решений в условиях неопределенности на ЭВМ.
Решение задач принятия решений на основе метода анализа иерархий
Методологию метода анализа иерархий (МАИ) можно представить как оперативное вмешательство в процесс выработки решения: после разработки с помощью систем поддержки принятия решений (СППР). Метод называют методом «раннего прототипирования при спиральном цикле разработки», потому что прототип опробывается пользователем на каждом витке спирали осознания проблемы, чтобы снизить вероятность ошибки в законченной системе (модели). Кроме того, в случае, когда необходимы оперативные изменения в сложных моделях, это становится главным условием использования моделей.
Методика решения задач
1. Очертить проблему и определить цель решения проблемы (задачи).
|
|
|
2. Построить иерархию, начиная с вершины (цели — с точки зрения управления), через промежуточные уровни (критерии, по которым зависят последующие уровни) к самому нижнему уровню (который обычно является перечнем альтернатив).
3. Построить множество матриц парных сравнений для каждого из нижних уровней — по одной матрице для каждого элемента примыкающего сверху уровня. Этот элемент называют направляемым по отношению к элементу, находящемуся на нижнем уровне, так как элемент нижнего уровня влияет на расположенный выше элемент. В полной простой иерархии любой элемент воздействует на каждый элемент примыкающего сверху уровня. Элементы любого уровня сравниваются друг с другом относительно их воздействия на направляемый элемент. Таким образом, получаем квадратную матрицу суждений. Попарные сравнения проводятся в терминах доминирования одного из элементов над другим, по отношению к их воздействию («весу», или «интенсивности») на общую для них характеристику. Эти суждения затем выражаются в целых числах с использованием табл.1 для величин суждений. Если элемент А1 доминирует над элементом А2, то клетка, соответствующая строке А1 и столбцу А2, заполняется целым числом, а клетка, соответствующая строке А2 и столбцу А1, заполняется обратным к нему числом (дробью). Если элемент А2 доминирует над элементом А1, то происходит обратное: целое число ставится в позицию А2, А1, а обратная величина автоматически в позицию А1, А2. Если считается, что А1 и А2 одинаковы, в обе позиции ставится единица.
|
|
|
Таблица 1
Шкала относительной важности
| Интенсивность относительной важности | Качественная оценка интенсивности относительной важности | Пояснения |
| 1 | Равная важность | Равный вклад двух объектов (деятельности) в цель |
| 3 | Умеренное превосходство одного над другим | Опыт и суждения дают легкое превосходство одного объекта (вида деятельности) над другим |
| 5 | Существенное или сильное превосходство | Опыт и суждения дают сильное превосходство одного объекта (вида деятельности) над другим |
| 7 | Значительное превосходство | Один объект (вида деятельности) имеет настолько сильное превосходство, что оно становится практически значительным |
| 9 | Очень сильное превосходство | Очевидность превосходства одного объекта (вида деятельности) над другим подтверждается наиболее сильно |
| 2,4, 6, 8 | Промежуточные решения между двумя соседними суждениями | Применяются в компромиссном случае |
| Обратные величины приведенных выше чисел | Если при сравнении одного объекта (вида деятельности) с другим получено одно из приведенных выше чисел (например 3), то при сравнении второго объекта (вида деятельности) с первым получим обратную величину (т.е. 1/3) |
|
|
|
Парные сравнения приводят к матричной форме — квадратной таблице, в которой числа могут быть расположены следующим образом:
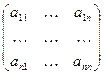
Эта матрица имеет свойства обратной симметричности, т.е.
aji=1/aij,
где индексы i и j относятся к строке и столбцу соответственно.
Если A1, A2, …,An - множество из n элементов и w 1 , w 2 ,…, wn - соответственно их веса, или интенсивности. С использованием МАИ сравним вес, или интенсивность, каждого элемента с весом, или интенсивностью, любого другого элемента множества по отношению к общему для них свойству или цели. При этом сравнение веса элемента A1 с весом элемента A2 можно представить как w 1 / w 2 , что означает сравнение, но не деление весов указанных элементов. Сравнение весов можно представить следующим образом:
| A1 | A2 | A3 | … |
| |||
| A1 | w1/w1 | w1/w2 | w1/w3 | … |  w1/wn w1/wn
| ||
| A2 | w2/w1 | w2/w2 | w2/w3 | … | w2/wn | ||
| A3 | w3/w1 | w3/w2 | w3/w3 | … | w3/wn | ||
| … | … | … | … | … | … | ||
| An | wn /w1 | wn /w2 | wn /w3 | … | wn /wn |
|
Отметим, что матрица может состоять только из одной строки или одного столбца, которые называются векторами.
При проведении оценок следует иметь в виду все сравниваемые элементы, чтобы сравнения были релевантными. Для проведения обоснованных численных сравнений не следует сравнивать более чем 7±2 элементов. В некоторых задачах с большим числом альтернатив не всегда нужно проводить парные сравнения между ними. Вместо этого вводится субкритерии (например, высокий, средний, низкий) и устанавливаем важность этих субкритериев по отношению к критериям. Затем берем каждую альтернативу, проверяем, который из субкритериев описывает ее наилучшим образом, и принимаем приоритет этого субкритерия. Далее складываем все приоритеты для этой альтернативы, и, наконец, нормализуем величины альтернатив, чтобы получить их общий приоритет.
4. На этапе 3 для получения каждой матрицы требуется n(n-1)/2 суждений (напомним, что при каждом парном сравнении автоматически приписываются обратные величины).
Когда проблемы представлены иерархически, матрица составляется для сравнения относительной важности критериев на втором уровне но отношению к общей цели на первом уровне. Подобные матрицы должны быть построены для парных сравнений каждой альтернативы на третьем уровне по отношению к критериям второго уровня. Матрица составляется, если записать сравниваемую цель (или критерий) вверху и перечислить сравниваемые элементы слева и сверху.
5. После проведения всех парных сравнений и ввода данных по собственному значению определить согласованность. Затем, используя отклонение λmax от n, проверить индекс согласованности, далее, сравнивая с соответствующими средними значениями для случайных элементов, получить отношение согласованности.
6. Этапы 3, 4 и 5 провести для всех уровней и групп в иерархии.
7. Использовать иерархический синтез для взвешивания собственных векторов весами критериев и вычислить сумму по всем соответствующим взвешенным компонентам собственных векторов уровня иерархии, лежащего ниже.
8. Найти согласованность всей иерархии, перемножая каждый индекс согласованности на приоритет соответствующего критерия и суммируя полученные числа. Результат затем разделить на выражение такого же типа, но со случайным индексом согласованности, соответствующим размерам каждой взвешенной приоритетами матрицы. Отметим, во-первых, что приемлемым является отношение согласованности (ОС) около 10% или менее. В противном случае качество суждений следует улучшить, возможно, пересмотрев способ, следуя которому задаются вопросы при проведении парных сравнений. Если это не поможет улучшить согласованность, то, вероятно, задачу следует более точно структурировать, т.е. сгруппировать аналогичные элементы под более значащими критериями. Потребуется возврат к этапу 2, хотя пересмотра могут потребовать только сомнительные части иерархии.
Пример решения задачи с помощью МАИ
Постановка задачи. Сельхозпредприятие (агрофирма) изучает возможность замены системы освещения производственных помещений ремонтных мастерских (РМ) технического обслуживания и ремонта (ТОиР) машин сельхозпредприятия или агрофирмы. В результате обсуждения удалось определить восемь критериев, которым, как казалось, должна удовлетворять система освещения. Эти критерии можно разбить на три кластера: экономический, технический и эксплуатационный. Хотя можно было начать с исследования сравнительной важности кластеров, руководители организации решили для более качественного анализа определять сравнительную важность всех факторов, не имея дела с кластерами. Задача заключалась в выборе одного из трех вариантов проектов системы освещения РМ:
вариант А – проект системы освещения на основе светодиодных панелей и светодиодных ламп с выносом в отдельные щиты выпрямительных устройств;
вариант Б - проект системы освещения на основе люминесцентных ламп в качестве общего освещения и светодиодных ламп для местного (люминесцентные энергосберегающие лампы для местного освещения не могут быть использованы из-за пульсации светового потока);
вариант В - проект системы освещения на основе люминесцентных ламп в качестве общего освещения и ламп накаливания для местного.
Первый шаг состоит в декомпозиции и представлении задачи в иерархической форме. На первом (высшем) уровне находится общая цель — проект системы освещения РМ (для краткости просто «Проект»). На втором уровне находятся восемь факторов или критериев, уточняющих цель, и на третьем (нижнем) уровне находятся три варианта проект системы освещения РМ, которые должны быть оценены по отношению к критериям второго уровня. Далее следует определение критериев и графическое представление иерархии (рис.1).








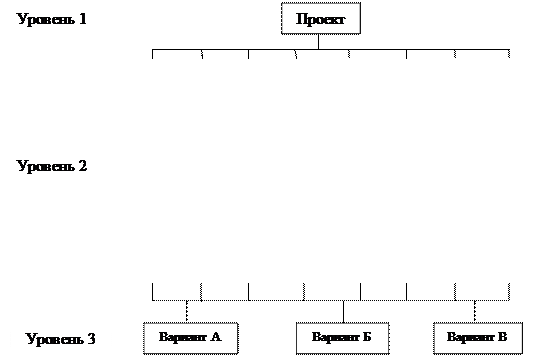
Рис.1. Декомпозиция задачи в иерархию
У руководителей агрофирма были следующие критерии:
1. Массово-габаритные размеры: длина проводки; потребное количество и размещение электрощитов; удобство работы; общая площадь помещений, количество рабочих мест, весовые характеристики электрооборудования.
2. Тип электроламп: тип электроламп, применяемых для освещения, их основные технико-эксплуатационные характеристики.
3. Освещенность помещений: соответствие освещенности зрительной работе в различных условиях для различных помещений (определяется параметрами: объект различия; фон; необходимость обеспечения равномерного распределения яркости рабочей поверхности, а также в пределах окружающего пространства и др. см. [2])
4. Дата выпуска: не нуждается в объяснении.
5. Срок исполнения: время на проектирование и установку системы освещения.
6. Перспектива: возможность подключения к системе освещения других помещений при расширении ремонтных мастерских в перспективе.
7. Потребляемая мощность: возможность по обеспечению энергосбережения.
8. Финансовые условия: стоимость проекта освещения, условия продажи и банковский кредит, порядок поставки, гарантийный срок эксплуатации, затраты при эксплуатации.
Второй шаг. Использование принципа дискриминации и сравнительных суждений.
1) Проводим парные сравнения с использованием табл.1. Потребуется девять квадратных матриц, одна для второго уровня иерархии и восемь — для третьего уровня. Эти матрицы представлены в табл.2 и табл. 3.При составлении таблиц использованы данные по 3 вариантам «Проекта».
Таблица 2
Проект системы освещения: матрица попарных сравнений для уровня 2
(для уровня критериев)
| Общее удовлетворение «Проектом» | Массово-габаритные размеры | Тип электроламп | Освещенность помещений | Дата выпуска | Срок исполнения | Перспектива | Потребляемая мощность | Финансовые условия |
| Массово-габаритные размеры | 1 | 5 | 3 | 7 | 6 | 6 | 1/3 | 1/4 |
| Тип электроламп | 1/5 | 1 | 1/3 | 5 | 3 | 3 | 1/5 | 1/7 |
| Освещенность помещений | 1/3 | 3 | 1 | 6 | 3 | 4 | 6 | 1/5 |
| Дата выпуска | 1/7 | 1/5 | 1/6 | 1 | 1/3 | 1/4 | 1/7 | 1/8 |
| Срок исполнения | 1/6 | 1/3 | 1/3 | 3 | 1 | 1/2 | 1/5 | 1/6 |
| Перспектива | 1/6 | 1/3 | 1/4 | 4 | 2 | 1 | 1/5 | 1/6 |
| Потребляемая мощность | 3 | 5 | 1/6 | 7 | 5 | 5 | 1 | 1/2 |
| Финансовые условия | 4 | 7 | 5 | 8 | 6 | 6 | 2 | 1 |
Теперь перейдем к парным сравнениям элементов на нижнем уровне (см.табл.3). Сравниваемые попарно элементы — это возможные варианты выбора «Проекта». Сравнивается, насколько более желателен или хорош тот или иной вариант для удовлетворения каждого критерия второго уровня. Получаем восемь матриц суждений размерностью 3х3, поскольку имеется восемь критериев на втором уровне и три возможных варианта проекта системы освещения, которые попарно сравниваются по каждому из критериев. Матрицы вновь содержат суждения руководителей агрофирмы.
Таблица 3
Проект системы освещения: матрицы попарных сравнений для уровня 3
(для уровня вариантов)
| Массово-габаритные размеры | А Б В | Тип электроламп | А Б В |
| А | 1 6 8 | А | 1 7 1/5 |
| Б | 1/6 1 4 | Б | 1/7 1 1/8 |
| В | 1/8 1/4 1 | В | 5 8 1 |
| Освещенность помещений | А Б В | Дата выпуска | А Б В |
| А | 1 8 6 | А | 1 1 1 |
| Б | 1/8 1 1/4 | Б | 1 1 1 |
| В | 1/6 4 1 | В | 1 1 1 |
| Срок исполнения | А Б В | Перспектива | А Б В |
| А | 1 5 4 | А | 2 1/2 1/2 |
| Б | 1/5 1 1/3 | Б | 2 1 1 |
| В | 1/4 3 1 | В | 2 1 1 |
| Потребляемая мощность | А Б В | Финансовые условия | А Б В |
| А | 1 6 8 | А | 1 1/7 1/5 |
| Б | 1/6 1 5 | Б | 7 1 3 |
| В | 1/8 1/5 1 | В | 5 1/3 1 |
3 шаг. Синтез приоритетов. Вычислить множество собственных векторов для каждой матрицы, а затем нормировать (нормализовать) результат к единице, получая тем самым вектор приоритетов. Используем для этого геометрическое среднее. Перемножаем элементы в каждой строке и извлекаем корни n-й степени, где n - число элементов. Итак, составляем матрицу следующего вида (для n=8):
|
| A1 | A2 | … |  A8 A8
| |||
| A1 | w1/w1 | w1/w2 | … | w1/w8 | ||
| A2 | w2/w1 | w2/w2 | … | w2/w8 | ||
| A3 | w3/w1 | w3/w2 | … |
 w3/w8 w3/w8
| ||
| … | … | … | … | … | ||
| A8 | w8/w1 | w8/w2 | … | w8/w8 |
Причем компонента собственного вектора первой строки равна:
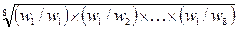 ,
,
компонента собственного вектора третьей строки равна
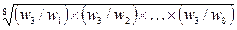 .
.
После того как компоненты собственного вектора получены для всех n строк, становится возможным их использование для дальнейших вычислений. Полученный таким образом столбец чисел нормируется делением каждого числа на сумму всех чисел по следующему образцу для n=8.
матрица вычислите оценки компонент нормализуйте результат для
собственного вектора получения оценки вектора
по строкам приоритетов
 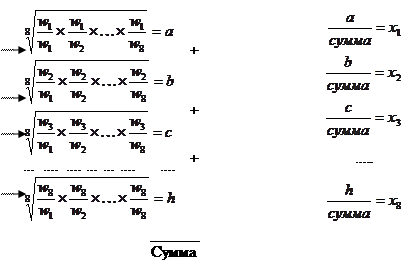 |
| A1 | A2 | … | A8 | |||
| A1 | w1/w1 | w1/w2 | … | w1/w8 | ||
| A2 | w2/w1 | w2/w2 | … | w2/w8 | ||
| A3 | w3/w1 | w3/w2 | … | w3/w8 | ||
| … | … | … | … |
| ||
| A8 | w8/w1 | w8/w2 | … | w8/w8 |
Умножение матрицы на вектор приоритетов производится следующим образом: умножаем первый элемент строки на первый элемент столбца x-в; второй элемент в строке на второй элемент столбца x-в, и т.д. Затем суммируем эти величины и получаем одно число для этой строки (показано для n=8):
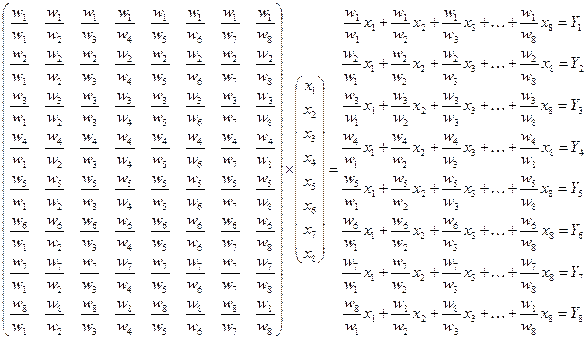
Когда матрица имеет такой вид, получается, что в действительности x1, х2, x3, и т.д., есть не что иное, как w1, w2, w3 и т.д. соответственно. Из отношений wi/wj определим каждую компоненту w. Важно отметить, что в матрице суждений нет отношения в виде wi/wj, а имеются только целые числа или их обратные величины из шкалы. Эта матрица в общем случае несогласованна. Алгебраически задача в случае согласованности заключается в решении уравнения Aw=nw, A =(wi/wj), а общая задача с обратносимметричными суждениями заключается в решении уравнения A'w'=λmax·w’, А'=(aij), где λmax — наибольшее собственное значение матрицы суждений А.
Вычислим вектор приоритетов (см. табл.4).
Дата добавления: 2019-09-13; просмотров: 4134; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
