Интеграл от функции комплексного переменного
Рассмотрим однозначную функцию  , определенную и непрерывную в области
, определенную и непрерывную в области  . Пусть
. Пусть  - кусочно-гладкая дуга линии, которая целиком принадлежит области
- кусочно-гладкая дуга линии, которая целиком принадлежит области  ; дуга
; дуга  ограничена точками
ограничена точками  (начальная) и
(начальная) и  (конечная). Разделим дугу
(конечная). Разделим дугу  на
на  элементарных дуг, занумеруем точки деления
элементарных дуг, занумеруем точки деления  в направлении от точки
в направлении от точки  до конечной точки
до конечной точки  , причем
, причем  . Введем обозначения:
. Введем обозначения: 
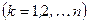 ,
,  . На каждой элементарной дуге
. На каждой элементарной дуге  выберем одну точку
выберем одну точку  (один из концов или внутреннюю точку) и запишем сумму
(один из концов или внутреннюю точку) и запишем сумму


Интегралом от функции  по дуге
по дуге  называется конечный предел суммы
называется конечный предел суммы 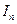 при
при 

Интеграл от функции комплексной переменной имеет следующие свойства.
1. 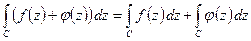
2. 
3. Если дуга 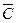 геометрически совпадает с дугой
геометрически совпадает с дугой  , но имеет направление, противоположное направлению дуги
, но имеет направление, противоположное направлению дуги  (для
(для 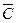 начальная точка
начальная точка  , а конечная
, а конечная  ) , то
) , то
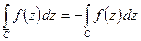 .
.
4. Если дуга  состоит из дуг
состоит из дуг  , то
, то
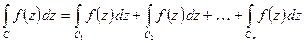
5. 
6. Если  во всех точках дуги
во всех точках дуги  и длина дуги
и длина дуги  равна
равна 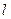 , то
, то

7. 
Вычисление интеграла
Вычисление интеграла от однозначной функции  комплексной переменной
комплексной переменной  сводится к вычислению обычных криволинейных интегралов
сводится к вычислению обычных криволинейных интегралов

Интеграл  вообще говоря зависит от пути интегрирования
вообще говоря зависит от пути интегрирования  .
.
Если  - аналитическая функция в односвязной области
- аналитическая функция в односвязной области  , то значение интеграла
, то значение интеграла  не зависит от линии
не зависит от линии  , а только от начальной и конечной точки этой линии.
, а только от начальной и конечной точки этой линии.
Теорема Коши.
Для всякой функции  , аналитической в некоторой односвязной области
, аналитической в некоторой односвязной области  , интеграл
, интеграл  по любому кусочно-гладкому замкнутому контуру
по любому кусочно-гладкому замкнутому контуру  , целиком принадлежащему области
, целиком принадлежащему области 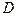 , равен нулю
, равен нулю
|
|
|

Если кривая  задана параметрическими уравнениями
задана параметрическими уравнениями  ,
,  ,
,  , то
, то

где  .
.
Если функция  аналитическая в однозначной области
аналитическая в однозначной области  , содержащей точки
, содержащей точки  и
и  , то справедлива формула Ньютона-Лейбница
, то справедлива формула Ньютона-Лейбница

Если функции  и
и  - аналитические в односвязной области
- аналитические в односвязной области  , а
, а  и
и  - произвольные точки этой области, то справедлива формула интегрирования по частям
- произвольные точки этой области, то справедлива формула интегрирования по частям

Пример. Вычислить интеграл  , где 1. линия
, где 1. линия  - отрезок действительной оси, соединяющей точки
- отрезок действительной оси, соединяющей точки  ,
,  , 2.
, 2.  - верхняя полуокружность
- верхняя полуокружность  .
.
Поскольку для комплексного числа  сопряженным является число
сопряженным является число  , то на действительной оси
, то на действительной оси  ,
, 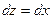 и
и  . Поэтому в первом случае
. Поэтому в первом случае

2. Верхнюю полуокружность  можно задать так.
можно задать так. 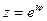 , где
, где 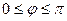 , причем
, причем  убывает. Поскольку
убывает. Поскольку 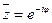 ,
,  , то
, то

Интегральная формула Коши
Если функция  является аналитической в области
является аналитической в области 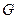 , ограниченной кусочно-гладким контуром
, ограниченной кусочно-гладким контуром  , и на самом контуре, то верна интегральная формула Коши
, и на самом контуре, то верна интегральная формула Коши
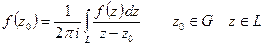
где  - любая точка внутри контура и контур
- любая точка внутри контура и контур  обходится так, чтобы область
обходится так, чтобы область 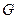 все время оставалась слева (обход контура против часовой стрелки).
все время оставалась слева (обход контура против часовой стрелки).
Таким образом, аналитическую функцию достаточно определить на контуре  , а по этой формуле можно автоматически получить ее значения в других точках
, а по этой формуле можно автоматически получить ее значения в других точках 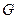 .
.
|
|
|
Если функция  аналитическая в области
аналитическая в области  и на ее границе
и на ее границе  , то для любого натурального
, то для любого натурального  верна формула
верна формула

 - значение
- значение  производной функции
производной функции  в точке
в точке  .
.
Это позволяет вычислить следующие интегралы


Пример. Вычислить интеграл  , где
, где  - окружность радиуса
- окружность радиуса  с центром в точке
с центром в точке 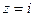 , причем обход контура осуществляется против часовой стрелки.
, причем обход контура осуществляется против часовой стрелки.
Преобразуем подынтегральную функцию следующим образом

Функция 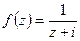 является аналитической внутри рассматриваемого круга и на его границе. Поэтому запишем
является аналитической внутри рассматриваемого круга и на его границе. Поэтому запишем

Степенные ряды. Ряд Тейлора.
Функция  , однозначная и аналитическая в точке
, однозначная и аналитическая в точке  , разлагается в окрестности этой точки в ряд Тейлора
, разлагается в окрестности этой точки в ряд Тейлора
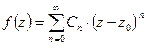
коэффициенты которого определяются формулами

где  - окружность с центром в точке
- окружность с центром в точке  , расположенная в окрестности точки
, расположенная в окрестности точки  , в которой функция
, в которой функция  аналитическая. Центр окружности круга сходимости находится в точке
аналитическая. Центр окружности круга сходимости находится в точке  ; эта окружность проходит через особую точку
; эта окружность проходит через особую точку  функции
функции  , ближайшую к точке
, ближайшую к точке  , т.е. радиус сходимости ряда будет равен расстоянию от точки
, т.е. радиус сходимости ряда будет равен расстоянию от точки  до ближайшей особой точки функции
до ближайшей особой точки функции  .
.
Для функций  ,
, 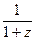 ,
,  ,
,  ряд Тейлора имеет следующий вид:
ряд Тейлора имеет следующий вид:


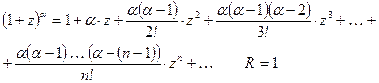

Пример. Разложить в ряд Тейлора функцию  в окрестности точки
в окрестности точки  .
.
|
|
|
Преобразуем эту функцию следующим образом 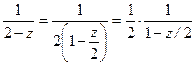 . Поскольку
. Поскольку  , то при
, то при 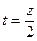 получим
получим

Следовательно,

Полученный ряд сходится при  , или
, или 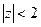 .
.
Ряд Лорана
Функция  однозначная и аналитическая в кольце
однозначная и аналитическая в кольце 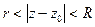 (не исключены случаи
(не исключены случаи  ,
,  ) , разлагается в ряд Лорана
) , разлагается в ряд Лорана

коэффициенты которого определяются формулой

где  - произвольная окружность с центром в точке
- произвольная окружность с центром в точке  , расположенная внутри этого кольца.
, расположенная внутри этого кольца.
В формуле Лорана ряд 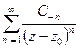
называется главной частью ряда Лорана, а ряд 
называется правильной частью ряда Лорана.
Пример. Разложить функцию 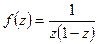 в ряд Лорана в следующих кольцах 1.
в ряд Лорана в следующих кольцах 1.  ; 2.
; 2. 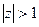 ; 3.
; 3. 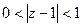 .
.
Во всех кольцах данная функция является аналитической и поэтому может быть разложена в них в соответствующий ряд Лорана. Представим эту функцию в виде суммы элементарных дробей:  .
.
1. Поскольку  , то получим
, то получим

Главная часть ряда Лорана имеет только один член.
2. Если 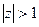 , то
, то  , поэтому
, поэтому

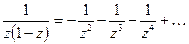
В этом разложении отсутствует правильная часть
3. Если 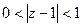 , то функцию
, то функцию 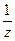 нужно разложить в геометрический ряд со знаменателем
нужно разложить в геометрический ряд со знаменателем  :
:

Главная часть полученного ряда Лорана содержит только один член.
Особые точки
Рассмотрим функцию 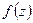 , аналитическую в точке
, аналитическую в точке  . Точка
. Точка  называется нулем функции
называется нулем функции 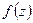 порядка (или кратности)
порядка (или кратности) 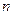 , когда выполняются условия:
, когда выполняются условия:
|
|
|

Если 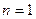 , то точка
, то точка  называется простым нулем.
называется простым нулем.
Значение  тогда и только тогда является нулем
тогда и только тогда является нулем  порядка функции
порядка функции  , аналитической в точке
, аналитической в точке  , когда в некоторой ее окрестности верно равенство
, когда в некоторой ее окрестности верно равенство

где  - функция, аналитическая в точке
- функция, аналитическая в точке  и
и  .
.
Особой точкой функции 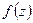 называется точка
называется точка  , в которой эта функция не является аналитической. Точка
, в которой эта функция не является аналитической. Точка  называется изолированной особой точкой функции
называется изолированной особой точкой функции 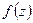 , когда существует окрестность этой точки, в которой
, когда существует окрестность этой точки, в которой  аналитическая всюду, кроме
аналитическая всюду, кроме  . Особая точка
. Особая точка  функции
функции 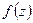 называется устранимой, когда существует конечный предел этой функции в данной точке:
называется устранимой, когда существует конечный предел этой функции в данной точке:  . Точка
. Точка  называется полюсом функции
называется полюсом функции 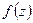 , когда
, когда 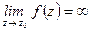 .
.
Для того, чтобы точка  была полюсом функции
была полюсом функции 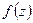 необходимо и достаточно, чтобы эта точка была нулем функции
необходимо и достаточно, чтобы эта точка была нулем функции

Точку  называют полюсом порядка
называют полюсом порядка  функции
функции  , когда эта точка является нулем порядка
, когда эта точка является нулем порядка 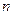 для функции
для функции  . В случае
. В случае  полюс называется простым.
полюс называется простым.
Для того, чтобы точка  являлась полюсом порядка
являлась полюсом порядка 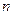 функции
функции  , необходимо и достаточно, чтобы функцию
, необходимо и достаточно, чтобы функцию 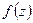 можно было привести к виду:
можно было привести к виду:

где  - функция, аналитическая в точке
- функция, аналитическая в точке  и
и  .
.
Точка  называется существенно особой точкой функции
называется существенно особой точкой функции  , когда в ней функция
, когда в ней функция 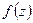 не имеет ни конечного ни бесконечного предела.
не имеет ни конечного ни бесконечного предела.
Справедливы следующие утверждения.
1. Точка  является устранимой особой точкой функции
является устранимой особой точкой функции  тогда и только тогда, когда ее лорановское разложение в окрестности точки
тогда и только тогда, когда ее лорановское разложение в окрестности точки  не содержит главной части.
не содержит главной части.
2. Точка  является полюсом функции
является полюсом функции 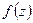 тогда и только тогда, когда главная часть ее лорановского разложения в окрестности точки
тогда и только тогда, когда главная часть ее лорановского разложения в окрестности точки  содержит только конечное число членов:
содержит только конечное число членов:

Наибольший из показателей степени разности  в знаменателях совпадает с порядком полюса.
в знаменателях совпадает с порядком полюса.
3. Точка  называется существенно особой точкой функции
называется существенно особой точкой функции  тогда и только тогда, когда главная часть ее лорановского разложения в окрестности точки
тогда и только тогда, когда главная часть ее лорановского разложения в окрестности точки  содержит бесконечное множество членов.
содержит бесконечное множество членов.
Пример. Показать, что точка  является нулем второго порядка для функции
является нулем второго порядка для функции  .
.
Разложим в ряды данную функцию и ее первую и вторую производные



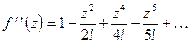
Поскольку  ,
,  ,
,  , т.е. выполняются условия
, т.е. выполняются условия

при  , то точка
, то точка  - нуль второго порядка для функции
- нуль второго порядка для функции  .
.
Вычеты функций
Вычетом однозначной аналитической функции 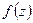 в изолированной особой точке
в изолированной особой точке  называется число, которое обозначается через
называется число, которое обозначается через 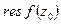 и определяют формулой
и определяют формулой
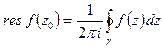
где интеграл взят в положительном направлении по контуру  . Используются и другие обозначения
. Используются и другие обозначения  ,
,  . В качестве контура
. В качестве контура  рассматривается окружность с центром в точке
рассматривается окружность с центром в точке  достаточно малого радиуса, такого, чтобы окружность не выходила за пределы области аналитичности функции
достаточно малого радиуса, такого, чтобы окружность не выходила за пределы области аналитичности функции  и не содержала внутри себя других особых точек этой функции. Вычет функции равен коэффициенту при минус первой степени лорановском разложении функции
и не содержала внутри себя других особых точек этой функции. Вычет функции равен коэффициенту при минус первой степени лорановском разложении функции  в окрестности точки
в окрестности точки 

Вычет функции в устранимой особой точке равен нулю.
Если  - полюс
- полюс 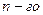 порядка функции
порядка функции 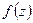 , то
, то

В случае простого полюса (  )
)

Если функция 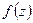 в окрестности точки
в окрестности точки  является частным двух аналитических функций
является частным двух аналитических функций

причем  ,
,  , а
, а  , т.е.
, т.е.  - простой полюс функции
- простой полюс функции  , то
, то

Если  является существенно особой точкой функции
является существенно особой точкой функции  , то для нахождения
, то для нахождения  необходимо найти коэффициент
необходимо найти коэффициент  в лорановском разложении функции
в лорановском разложении функции  в окрестности точки
в окрестности точки  ; это и будет
; это и будет  .
.
Теорема Коши.
Если функция 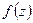 является аналитической на границе
является аналитической на границе  области
области  и всюду внутри этой области, за исключением конечного числа особых точек
и всюду внутри этой области, за исключением конечного числа особых точек  , то
, то

Этой теоремой пользуются при вычислении определенных интегралов и нахождении суммы рядов.
Функция 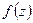 является аналитической в в бесконечно удаленной точке
является аналитической в в бесконечно удаленной точке  , если функция
, если функция  аналитична в точке
аналитична в точке 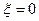 . Например, функция
. Например, функция  аналитична в точке
аналитична в точке 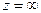 , поскольку функция
, поскольку функция  аналитична в точке
аналитична в точке 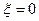 .
.
Пусть функция 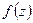 аналитична в некоторой окрестности бесконечно удаленной точки (кроме самой точки
аналитична в некоторой окрестности бесконечно удаленной точки (кроме самой точки 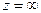 ). Говорят, что
). Говорят, что  является устранимой особой точкой, полюсом или существенно особой точкой в зависимости от того, конечен, бесконечен или вовсе не существует предел этой функции при
является устранимой особой точкой, полюсом или существенно особой точкой в зависимости от того, конечен, бесконечен или вовсе не существует предел этой функции при  .
.
Теорема. Если 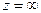 является устранимой особой точкой функции
является устранимой особой точкой функции  , то ее лорановское разложение в окрестности данной точки не содержит положительных степеней
, то ее лорановское разложение в окрестности данной точки не содержит положительных степеней 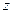 ; когда
; когда 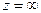 - полюс, то это разложение содержит конечное число положительных степеней
- полюс, то это разложение содержит конечное число положительных степеней 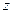 , в случае существенно особой точки – бесконечное множество положительных степеней
, в случае существенно особой точки – бесконечное множество положительных степеней 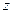 .
.
Рассмотрим функцию 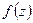 , аналитическую в некоторой окрестности точки
, аналитическую в некоторой окрестности точки  (кроме, быть может, самой этой точки).
(кроме, быть может, самой этой точки).
Вычетом функции 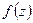 в бесконечности называется величина
в бесконечности называется величина

где  - окружность достаточно большого радиуса
- окружность достаточно большого радиуса  , которую точка
, которую точка  проходит по часовой стрелке (при этом окрестность точки
проходит по часовой стрелке (при этом окрестность точки  остается слева, как и в случае конечной точки
остается слева, как и в случае конечной точки  ).
).
Из этого определения следует, что вычет функции в бесконечности равен коэффициенту при  в лорановском разложении
в лорановском разложении 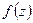 в окрестности точки
в окрестности точки  , взятому со знаком минус
, взятому со знаком минус

Известные разложения функций  ,
, 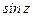 ,
,  ,
,  ,
,  можно рассматривать как лорановские ряды в окрестности точки
можно рассматривать как лорановские ряды в окрестности точки  . Поскольку указанные ряды содержат бесконечное множество положительных степеней
. Поскольку указанные ряды содержат бесконечное множество положительных степеней 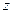 , то указанные функции имеют в точке
, то указанные функции имеют в точке 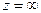 существенную особенность.
существенную особенность.
Теорема. Если функция 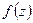 имеет в расширенной комплексной плоскости конечное число особых точек
имеет в расширенной комплексной плоскости конечное число особых точек  , то сумма всех ее вычетов, включая и вычет бесконечности, равен нулю.
, то сумма всех ее вычетов, включая и вычет бесконечности, равен нулю.
Пример. Найти вычет функции  .
.
Данную функцию можно записать так:  и рассматривать эту сумму как разложение в ряд Лорана по степеням
и рассматривать эту сумму как разложение в ряд Лорана по степеням 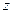 , для которого
, для которого  . Соответственно находим, что
. Соответственно находим, что  (
(  - особая точка) .
- особая точка) .
Дата добавления: 2019-09-13; просмотров: 755; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
