Дифференцирование функции комплексной переменной
Комплексные числа.
Комплексное число записывается в виде
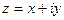
где 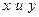 - действительные числа,
- действительные числа, 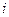 - мнимая единица
- мнимая единица 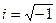 .
.
Комплексные числа записывают также в тригонометрической форме
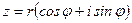
где, соответственно 
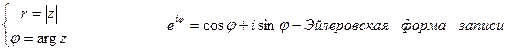
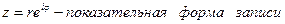 . Комплексно сопряженная форма комплексного числа -
. Комплексно сопряженная форма комплексного числа - 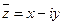 .
.
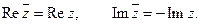
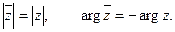
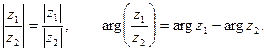
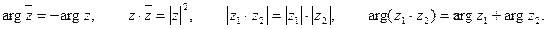
Действия над комплексными числами
Сложение и вычитание
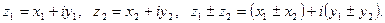
Умножение
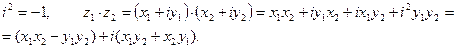
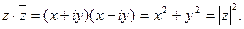
Деление
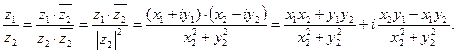
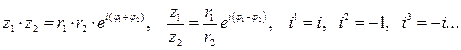
Возведение в степень 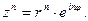
Извлечение корня 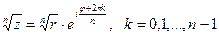
Примеры:
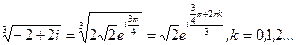
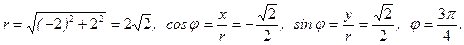
Понятие функции комплексного переменного
 Комплексное число имеет вид
Комплексное число имеет вид 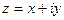 , где
, где 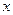 и
и 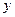 - действительные числа,
- действительные числа, 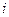 - мнимая единица
- мнимая единица 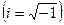 . Оно изображается точкой на комплексной плоскости с координатами
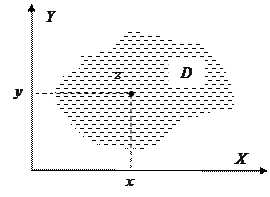
. Оно изображается точкой на комплексной плоскости с координатами 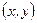 . Пусть
. Пусть 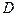 - область (открытое связанное множество) комплексной плоскости
- область (открытое связанное множество) комплексной плоскости 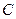 . Если каждой точке
. Если каждой точке 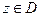 по определенному правилу
по определенному правилу 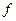 поставлено в соответствие единственное комплексное число
поставлено в соответствие единственное комплексное число 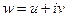 , то говорят, что в области
, то говорят, что в области 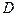 определена однозначная функция комплексной переменной
определена однозначная функция комплексной переменной 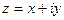 и пишут
и пишут 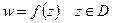 . Функцию
. Функцию 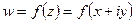 можно рассматривать как комплексную функцию двух действительных переменных
можно рассматривать как комплексную функцию двух действительных переменных 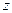 и
и 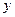 , определенную в области
, определенную в области 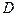 . Задание такой функции равносильно заданию двух действительных функций
. Задание такой функции равносильно заданию двух действительных функций 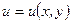 ,
, 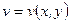
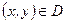 ,
, 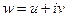 . Таким образом, если
. Таким образом, если 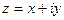 ,
, 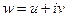 , то
, то
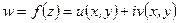
Комплексное число 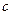 является пределом однозначной функции
является пределом однозначной функции 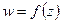 при
при 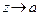 , если для всякого
, если для всякого 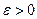 существует такое число
существует такое число 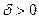 , что из неравенства
, что из неравенства 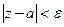 следует неравенство
следует неравенство 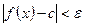 . В этом случае пишут
. В этом случае пишут 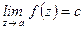 .
.
Функция 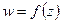 называется непрерывной в точке
называется непрерывной в точке 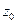 , если
, если
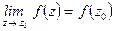
Функция, непрерывная в каждой точке области 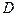 , называется непрерывной в этой области.
, называется непрерывной в этой области.
|
|
|
Область 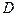 называется односвязной, когда она ограничена замкнутой линией
называется односвязной, когда она ограничена замкнутой линией 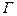 , не пересекающей себя. Область
, не пересекающей себя. Область 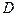 называется двусвязной, когда она ограничена двумя замкнутыми линиями
называется двусвязной, когда она ограничена двумя замкнутыми линиями 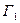 и
и 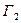 , которые не пересекаются и каждая не пересекает себя; внутренняя линия
, которые не пересекаются и каждая не пересекает себя; внутренняя линия 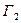 , в частности, может вырождаться в точку или в дугу непрерывной линии. Аналогично определяется трехсвязная, четырехсвязная и т.д. области.
, в частности, может вырождаться в точку или в дугу непрерывной линии. Аналогично определяется трехсвязная, четырехсвязная и т.д. области.
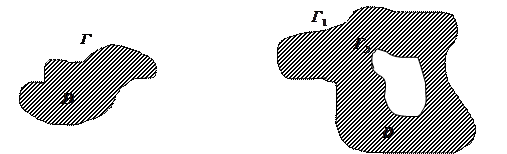 |
Пример. Найти значение функции
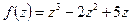 при следующих значениях аргумента: 1.
при следующих значениях аргумента: 1. 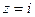 , 2.
, 2. 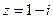 , 3.
, 3. 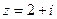 .
.
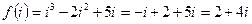
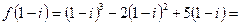
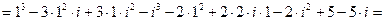
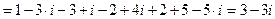
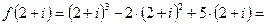
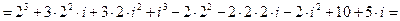
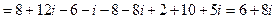
Элементарные функции комплексной переменной
Функции комплексной переменной 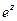 ,
, 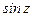 ,
, 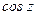 определяются как суммы соответствующих степенных рядов, сходящихся на всей комплексной плоскости:
определяются как суммы соответствующих степенных рядов, сходящихся на всей комплексной плоскости:
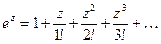
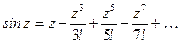
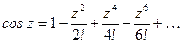
Показательная функция 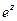 имеет следующие свойства: 1.
имеет следующие свойства: 1. 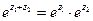 , где
, где 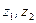 - произвольные комплексные числа, 2.
- произвольные комплексные числа, 2. 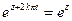
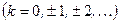 , т.е.
, т.е. 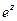 является периодической функцией с периодом
является периодической функцией с периодом 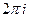 .
.
Тригонометрические функции 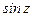 ,
, 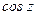 - периодические с действительным периодом
- периодические с действительным периодом 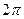 ; они имеют только действительные нули
; они имеют только действительные нули 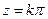 и
и 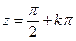 соответственно, где
соответственно, где 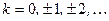 .
.
Для функций 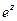 ,
, 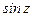 ,
, 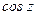 справедливы формулы Эйлера
справедливы формулы Эйлера

откуда

Если 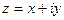 , то
, то 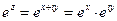 , поэтому
, поэтому
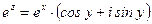
Тригонометрические функции 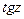 ,
, 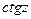 определяются формулами
определяются формулами
|
|
|
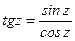 ,
, 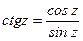
Все формулы тригонометрии остаются справедливыми и для тригонометрических функций комплексной переменной.
Гиперболические функции 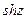 ,
, 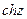 ,
, 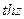 ,
, 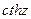 определяются формулами
определяются формулами
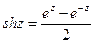 ,
, 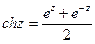 ,
, 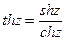 ,
, 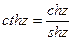
Функции 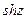 ,
, 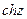 можно рассматривать как суммы степенных рядов, сходящихся на всей комплексной плоскости:
можно рассматривать как суммы степенных рядов, сходящихся на всей комплексной плоскости:
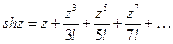
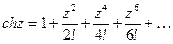
Тригонометрические и гиперболические функции связаны между собой следующими равенствами




Логарифмическая функция 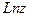 , где
, где 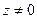 , определяется как функция, обратная показательной, причем
, определяется как функция, обратная показательной, причем
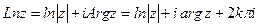
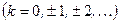
Эта функция является многозначной. Главным значением 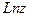 называется такое значение, которое получается при
называется такое значение, которое получается при 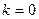 , оно обозначается через
, оно обозначается через 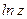 :
:
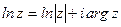
Очевидно, что
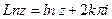
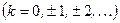
Справедливы следующие равенства
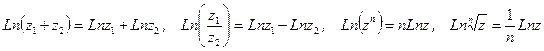
Обратные тригонометрические функции 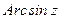 ,
, 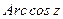 ,
, 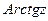 ,
, 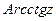 определяются как функции, обратные тригонометрическим функциям
определяются как функции, обратные тригонометрическим функциям 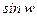 ,
, 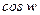 ,
, 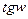 ,
, 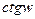 . Например, когда
. Например, когда 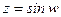 , то
, то  называется арксинусом числа
называется арксинусом числа 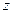 и обозначается
и обозначается 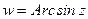 .
.
Все эти функции являются многозначными, они выражаются через логарифмические функции следующими формулами
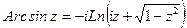
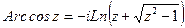
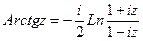
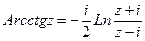
Главные значения обратных тригонометрических функций 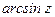 ,
, 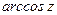 ,
, 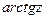 ,
, 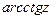 получаются, когда рассматриваются главные значения соответствующих логарифмических функций.
получаются, когда рассматриваются главные значения соответствующих логарифмических функций.
Общая степенная функция 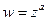 , где
, где 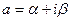 - любое комплексное число, определяется формулой
- любое комплексное число, определяется формулой
|
|
|
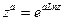
ее главное значение равно
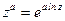
Общая показательная функция 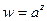 (
( 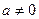 - любое комплексное число) определяется формулой
- любое комплексное число) определяется формулой
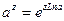
главное значение этой многозначной функции равно
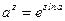
Пример. Найти 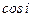 . Используя формулу для
. Используя формулу для 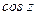 -
- 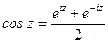 , получим
, получим
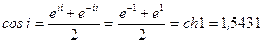
Дифференцирование функции комплексной переменной
Рассмотрим функцию 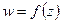 , определенную в некоторой области
, определенную в некоторой области 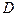 комплексной плоскости, и точки
комплексной плоскости, и точки 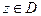 ,
, 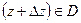 . Обозначим
. Обозначим 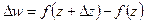 ,
, 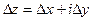 .
.
Производной функции 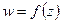 в точке
в точке 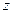 называется конечный предел отношения
называется конечный предел отношения 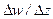 когда
когда 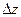 произвольным образом стремится к нулю
произвольным образом стремится к нулю
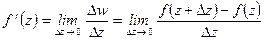
Функция, имеющая производную в точке 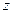 , называется дифференцируемой в этой точке.
, называется дифференцируемой в этой точке.
Если 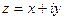 , то комплексная функция
, то комплексная функция 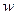 имеет вид
имеет вид 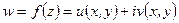 , и ее приращение
, и ее приращение 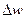 можно представить в виде
можно представить в виде
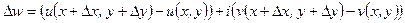
Таким образом, при любом способе стремления 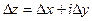 к нулю, должен существовать этот предел, равный одному и тому же комплексному числу
к нулю, должен существовать этот предел, равный одному и тому же комплексному числу 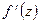 . В частности, это должно иметь место, если а)
. В частности, это должно иметь место, если а) 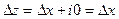 и
и 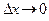 или, если б)
или, если б) 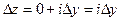 и
и 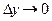 . В первом случае
. В первом случае
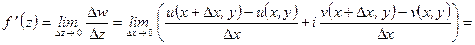
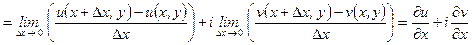
Во втором случае
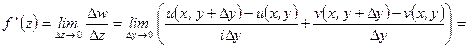
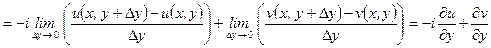
Но тогда должны выполняться равенства
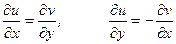 (А)
(А)
которые называют условиями Коши-Римана (или условиями Д’Аламбера-Эйлера).
Обратно, если в некоторой точке 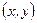 функции
функции 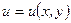 ,
, 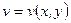 дифференцируемы как функции действительных переменных
дифференцируемы как функции действительных переменных 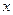 ,
, 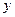 и, кроме того, удовлетворяют соотношениям (А), то функция
и, кроме того, удовлетворяют соотношениям (А), то функция 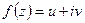 является дифференцируемой в точке
является дифференцируемой в точке 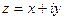 как функция комплексной переменной
как функция комплексной переменной 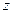 .
.
|
|
|
Функция 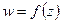 называется аналитической в точке
называется аналитической в точке 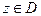 , если она дифференцируема в ней и некоторой ее окрестности. Функция
, если она дифференцируема в ней и некоторой ее окрестности. Функция 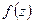 называется аналитической в области
называется аналитической в области 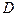 , если она дифференцируема в каждой ее точке.
, если она дифференцируема в каждой ее точке.
Для всякой аналитической функции 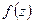 производная
производная 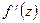 выражается через частные производные функций
выражается через частные производные функций 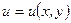 ,
, 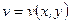 :
:
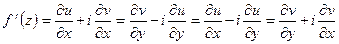
Геометрический смысл модуля и аргумента производной.
Если функция 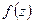 - аналитическая в точке
- аналитическая в точке 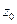 и
и 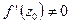 , то
, то 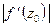 равен коэффициенту растяжения в точке
равен коэффициенту растяжения в точке 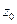 при отображении
при отображении 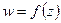 плоскости
плоскости 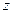 на плоскость
на плоскость 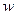 , точнее: при
, точнее: при 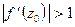 будет растяжение, а при
будет растяжение, а при 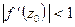 будет сжатие. Аргумент производной
будет сжатие. Аргумент производной 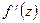 равен углу, на который надо повернуть касательную в точке
равен углу, на который надо повернуть касательную в точке 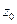 к любой гладкой кривой на плоскости
к любой гладкой кривой на плоскости 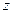 , которая проходит через точку
, которая проходит через точку 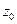 , чтобы получить направление касательной в точке
, чтобы получить направление касательной в точке 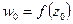 к образу этой кривой на плоскости
к образу этой кривой на плоскости 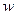 при отображении
при отображении 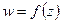 . Отметим, что при
. Отметим, что при 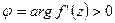 поворот осуществляется против часовой стрелки, а при
поворот осуществляется против часовой стрелки, а при 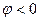 - по часовой стрелке.
- по часовой стрелке.
Отображение с помощью аналитической функции 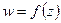 называется конформным отображением.
называется конформным отображением.
Дифференцирование элементарных функций.
Производные элементарных функций 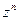 ,
, 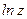 ,
, 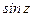 ,
, 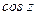 ,
, 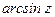 ,
, 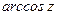 ,
, 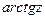 ,
, 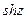 ,
, 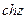 находятся по формулам:
находятся по формулам:
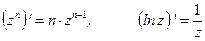
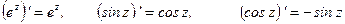
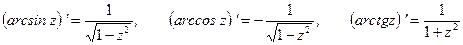
 .
.
Гармоническая функция.
Функция 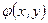 называется гармонической в области
называется гармонической в области 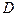 , если она имеет в ней непрерывные частные производные второго порядка и удовлетворяет в этой области уравнению Лапласа
, если она имеет в ней непрерывные частные производные второго порядка и удовлетворяет в этой области уравнению Лапласа
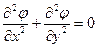
Если функция 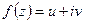 аналитическая в области
аналитическая в области 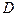 , то ее действительная часть
, то ее действительная часть 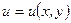 и мнимая часть
и мнимая часть 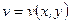 являются гармоническими функциями в этой области.
являются гармоническими функциями в этой области.
Однако, если 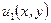 ,
, 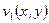 - две произвольные гармонические функции, то функция
- две произвольные гармонические функции, то функция 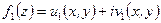 вовсе не обязана быть аналитической функцией: для аналитичности
вовсе не обязана быть аналитической функцией: для аналитичности 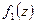 нужно, чтобы функции
нужно, чтобы функции 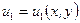 ,
, 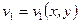 удовлетворяли условиям Коши-Римана.
удовлетворяли условиям Коши-Римана.
Пример. Выяснить, является ли аналитической функция 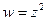 .
.
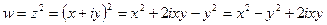 , т.е.
, т.е. 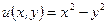 ,
, 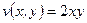 .
.
Находим частные производные
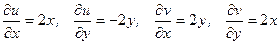
Следовательно, 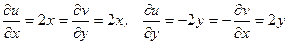 . Условие Коши-Римана выполнены для всех точек плоскости
. Условие Коши-Римана выполнены для всех точек плоскости 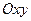 . Значит функция
. Значит функция 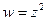 является аналитической на всей плоскости.
является аналитической на всей плоскости.
Дата добавления: 2019-09-13; просмотров: 151; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
