Элементы теории нечетких множеств

Стр 1 из 5Следующая ⇒

МИНИСТЕРСТВО ОБРАЗОВАНИЯ и НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Коломенский институт (филиал)

федерального государственного бюджетного образовательного учреждения

высшего образования

«МОСКОВСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра автоматизации производства и информационных технологий

П.С. Романов

Методические указания по выполнению лабораторной работы

По дисциплине

«СИСТЕМЫ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА»

Моделирование системы нечеткого вывода по Мамдани с помощью пакета SciFLT системы Scilab

Коломна – 2019

Содержание

1.	Введение ..........................................................................................................................	2
2.	Общие сведения о нечетком регулировании………………………………………	2
3.	Элементы теории нечетких множеств………………………………………………	3
4.	Основные понятия нечеткой логики………………………………………………..	6
5.	Применение теории нечетких множеств и нечеткой логики в задачах управления.	9
6.	Редактор системы нечеткого вывода. Построение нечетких систем в Scilab. Система нечеткого вывода по Мамдани……………………………………………...	12
7.	Задание для лабораторной работы..................................................................................	30
8.	Структура отчета..............................................................................................................	31
9.	Исходные данные………………………………………………………………………	31
10.	Литература........................................................................................................................	32

Введение

Лабораторная работа выполняется на основе теории нечетких множеств на ПК с использованием систем Scilab и Microsoft WORD в среде Windows ХР/7/8/10.

Цели работы:

изучение основ нечеткой (или фаззи) логики

изучение метода построения нечеткой системы в модуле SciFLT системы SciLAB;

получение умений и навыков:

построения системы нечеткого вывода по Мамдани с помощью пакета SciFLT системы Scilab;

в анализе полученных результатов.

Общие сведения о нечетком регулировании

В последние годы в автоматике, компьютерной технике, теории принятия решений, системах искусственного интеллекта используются модели и методы, основанные на теории нечетких множеств (ТНМ). Она возникла на стыке математической теории множеств и математической логики в середине 70-х годов. Ее первые основы были сформулированы в 1965 году американским математиком Л. Заде статье «Fuzzy Sets», название которой переводится на русский язык как «нечеткие множества». Слово «fuzzy” в русском языке получило перевод «нечеткий». У нас в стране используется наряду с понятием «нечеткий» слово «фаззи».

Благодаря дальнейшим разработкам и публикациям Л. Заде, Е. Мамдани, М. Сугено, выявился целый спектр возможностей применения ТНМ для задач принятия решений и управления, в которых объект и условия его функционирования недостаточно изучены, модель объекта и цель управления слабо формализованы. Постепенно сформировалась совокупность методов и приемов использования ТНМ, которую называют фаззи-технологией или фаззи-методологией. Оказалось, что она эффективна для управления не только cлa6o структурированными объектами, но и хорошо изученными, имеющими строгое математическое описание. Одновременно развивались новые направления науки, в которых так же, как и в фаззи-технологии, использовались знания, опыт и интуиция специалистов в данной области. К этим направлениям относятся экспертные системы, ситуационное управление, искусственные нейронные сети, системы искусственного интеллекта, системы, базирующиеся на знаниях (в англ. ‑ knowlеdge-based sуstems ). Фаззи-системы и фаззи-контроллеры применяются сегодня как для управления сложными технологическими процессами, так и для автоматизации простых бытовых приборов. В системе SciLAB имеется модуль SciFLT нечеткой логики.

Нечеткая методология в прикладных задачах автоматизации и управления служит средством достижения компромисса между двумя подходами к решению этих задач.

Традиционный подход к постановке и решению задач управления и регулирования основывается на предположениях, что модель объекта управления (ОУ) известна и задана в виде передаточных функций его отдельных каналов или в форме системы дифференциальных уравнений, связывающих его входные и выходные переменные, и что при известной цели управления алгоритм функционирования управляющего устройства (УУ) однозначно предопределяется этой моделью и целью управления. Причем, решается данная задача синтеза алгоритма УУ с помощью строгих аналитических методов математики.

Однако в реальной практике автоматизации сложных технологических процессов и производств редко удается построить достаточно точную математическую модель ОУ и применить строгую однозначную процедуру синтеза алгоритма управления. Поэтому большинство функционирующих в промышленности автоматических и автоматизированных систем управления создано с использованием не только методов теории управления, но и опыта и интуиции специалистов по автоматизации, эвристических знаний технологов.

Принцип функционирования и методология построения системы нечеткого регулирования показаны на схеме на рис 1.

Рис. 1. Функциональная структура системы нечеткого регулирования

Вся исходная информация о стратегии управления хранится в базе правил (в англ. ‑ rule-base) в виде правил условного логического вывода «ЕСЛИ…, ТО » (в aнгл. – «IF..., THEN…»), которые формулируются на основе тщательного изучения объекта и задачи управления, путем анкетного опроса специалистов-технологов, хорошо знающих объект управления. Центральным звеном нечеткого регулятора является блок нечёткого вывода (БНВ), или блок принятия решений (в англ. ‑ decision making), в котором на основе нечеткой информации о сигнале ошибки регулирования e делается вывод о соответствующем нечётком множестве значений управляющего воздействия у.

В блоке БНВ реализуется так называемая инференц-процедура, в процессе которой агрегируются (объединяются) выводы отдельных правил об управляющем воздействии. Результатом агрегирования являются «усеченные» нечёткие множества управляющих воздействий. В блоке нормирования (БН) измеренный четкий (в англ. – crisp) сигнал ошибки регулирования e умножением на масштабный коэффициент k_e_.н.<1 приводится к ограниченному интервалу (например, [-1,+1]). Блок фаззификации (БФ) определяет значение функции принадлежности, соответствующее нормированному значению e_н. Блоки дефаззификации (БДФ) и денормирования (БДН) выполняют обратные процедуры: по нескольким «усеченным» функциям принадлежности вычисляется четкое значение нормированного управляющего воздействия у_н и соответствующее ему ненормированное значение у = у_н/k_у.н. (k_у.н < 1).

Элементы теории нечетких множеств

В математике обычное понятие «множество» определяют как совокупность элементов, обладающих некоторым общим свойством. При этом заранее, аксиоматически, предполагают, что любой элемент либо принадлежит, либо не принадлежит данному множеству, а факт принадлежности или непринадлежности элемента x к множеству Х характеризуют с помощью функции m (х), которая принимает соответственно значения 1 (принадлежит) или 0 (не принадлежит). Однако во многих реальных задачах прикладных исследований и в повседневной практике такой жесткий, двузначный принцип классификации элементов недостаточно гибок для математического описания сложных явлений и процессов, не оправдан для формализации нестрогих понятий и высказываний, используемых в естественном языке. Например, такие лингвистические понятия, как «близко», «чуть больше», или лингвистические сообщения «температура в помещении нормальная», «в помещении прохладно», используемые в житейской и технологической практике, не могут быть описаны и проанализированы с помощью классических понятий теории множеств и математической логики.

Для того, чтобы адекватно представить приблизительное (словесное) описание свойств предметов и явлений на языке теории множеств, Л. Заде ввел понятие лингвистической переменной, значениями которой являются слова или фразы естественного языка. Например, если фактическая переменная ‑ температура x в жилом помещении (рис.2, а) ‑ характеризуется бытовыми понятиями «нормальная» (в диапазоне 19-21^оС), «прохладно» (17-19 °С) и т.д., то совокупность этих 5 значений «холодно», «прохладно», «нормально» и т.д. рассматривается как лингвистическая переменная х_l. При этом совокупность значений (названий!) лингвистической переменной x_l образует так называемое терм-множество, а исходная переменная x называется базовой.

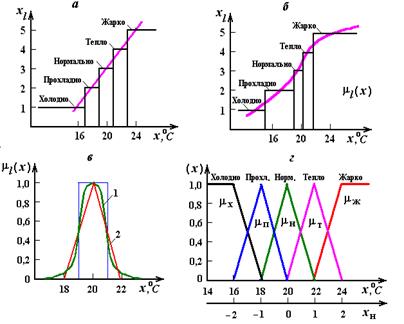
Рис.2. К понятиям "лингвистическая переменная" (а, б) и "функция принадлежности" (в, г)

Переход от абсолютных значений базовой переменной x к соответствующим значениям лингвистической переменной (см. рис. 2, 6) необязательно линеен (в обычном понимании) и что различным термам могут соответствовать разные диапазоны базовой переменной.

Ограничение на значения базовой переменной x, которое каждому ее значению ставит в соответствие число из интервала [0, 1], называется функцией принадлежности (ФП) (в англ. membership function) и обозначается m(х). На рис. 2,в в качестве примера показаны ФП m_l(х), определяющие терм «нормальная температура в помещении».

Линия 1 соответствует ФП, представленной в виде кривой Гаусса:

, (1)

где m = 20^оС, s » 1^оС.

Линия 2 соответствует наиболее часто используемой на практике треугольной форме ФП. На рис.2,г представлены пять функций треугольной и трапецеидальной формы, образующие терм-множество названий лингвистических значений переменной х_l ‑ «температура в помещении», т.е. индекс l в данном случае принимает значения «холодно», «прохладно» и т.д. Обычно на практике вместо абсолютных значений базовой переменной используют ее нормированные значения х_н, (см. рис.2,г). При этом достаточно удобной оказывается система из семиФП (рис. 3,а), которая охватывает следующие универсальные лингвистические значения (англ.): negative big (NB), negative medium (NM), negative small (NS), zero (ZR), positive small (PS), positive medium (PM), positive big (PВ).

Рис. 3. Унифицированные системы функции принадлежности для нормированных

значений переменной состояния (а), ошибки регулирования (б, тонкие линии)

и управляющего воздействия (б, вертикальные линии)

На рис. 3,б показана система из девяти ФП ошибки регулирования e, заданных на интервале [-1, 1]. Здесь, в отличие oт рис. 3, а, добавлены еще два лингвистических значения- negаtive zero (NZ) и positive zero (РZ), a интервалы для отдельных ФП приняты неодинаковыми. Для управляющего воздействия у ФП иногда могут иметь вполне однозначный характер, как показано на рис. 3,б (жирные линии).

Нечеткое множество (НМ) (в англ. ‑ fuzzy set) А, ‑ совокупность всех пар вида (х, m_А(х)) , которая образована из значений базовой переменной хÎХ и из функций принадлежности m_А(х), устанавливающих связь между этими значениями и числами в интервале [0, 1], т.е.: 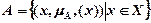(2)

Для приведенного выше примера с тепловым режимом в помещении (см. рис.2,г) существуют пять НМ, характеризуемых функциями m_l(х): m_ж(х) – «жарко», m_т(х) – «тепло» и т.д.

Множество А состоит из элементов, каждый из которых характеризуется парой значений (х_i, m_i(х)). Такую элементарную составляющую нечеткого множества называют синглтоном (в англ. ‑ singleton). Пример синглтона – дискретные значения функций m_l(у) на рис.3,б. Любое нечеткое множество А можно рассматривать как объединение синглтонов, которое в общем случае - для бесконечно большого количества элементов - обозначают так:

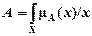(3)

Если НМ А состоит из конечного числа элементов, то вместо условного обозначения в виде интеграла (3) используют сумму:

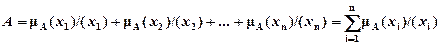(4)

Здесь, как и в выражении (3), знак дроби не означает деление, а суммирование (или интегрирование) соответствует принятой в теории множеств операции объединения, т.е.:

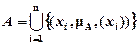(5)

Процедура введения терм-множеств А, их функций принадлежности m_А(х) и установления конкретного значения m_А(х*), соответствующего измеренному значению х*, называется фаззификацией.

Для НМ применимы все свойства и операции, используемые для обычных множеств. Так, НМ А и В равны друг другу, если равны их ФП m_А и m_В, т.е.:

А = В, если m_А (х) = m_B(х), хÎХ. (6)

Нечеткое множество А включает в себя НМ В, т.е.:

В Í А, если mB(х) £ mА(х), хÎХ . (7)

Нечетким объединением двух нечетких множеств А и В, заданных на общем базовом множестве Х , называют наименьшее нечеткое множество С, которое содержит одновременно как А, так и В и имеет вид:

С:= А ÈВ 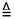{(х, m_А_È_В(х))½хÎХ}, (8)

где m_С(х) = m_А_È_В(х) = max{m_А(х), m_В(х)} (9)

Символы := и 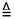означают «равно по определению». Нечетким пересечением двух нечетких множеств А и В , заданных на общем базовом множестве Х называют наибольшее нечеткое множество С, которое содержится одновременно и в А, и в В и имеет вид:

С:= А ÇВ 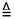{(х, m_А_Ç_В(х))½ хÎХ}, (10)

где m_С(х)= m_А_Ç_В(х) = min{m_А(х), m_В(х)} (11)

Нечетким дополнением нечеткого множества А, заданного на базовом множестве Х, называют нечеткое множество вида:

ØА 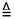{(х, m_Ø_А(х)}, (12)

где m_Ø_А(х) = 1- mА(х). (13)

Понятия объединения и пересечения, введенные для случая двух исходных множеств А и В, могут быть распространены и на случай нескольких исходных множеств.

На рис. 4 показано ФП производных НМ (8),(10),(12) из ФП m_А, m_В, m_с треугольной формы, характеризующих три исходных множества А,В,С на интервале [-2,+2].

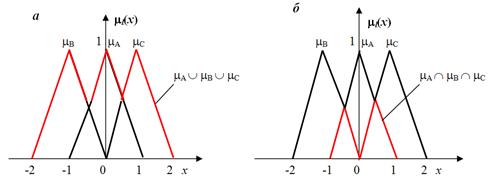
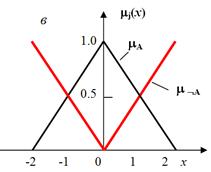
Рис. 4. Основные операции над нечеткими множествами

Дата добавления: 2019-09-13; просмотров: 349; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 Следующая ⇒

Мы поможем в написании ваших работ!