Операции с нечеткими множествами в модуле SciFLT
МИНИСТЕРСТВО ОБРАЗОВАНИЯ и НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Коломенский институт (филиал)
федерального государственного бюджетного образовательного учреждения
высшего образования
«МОСКОВСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра автоматизации производства и информационных технологий
П.С. Романов
Методические указания по выполнению лабораторной работы
По дисциплине
«СИСТЕМЫ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА»
Построение нечетких множеств в системе Scilab и операции над ними
Коломна – 2019
Содержание
| 1. | Введение .......................................................................................................................... | 2 |
| 2. | Построение функций принадлежности нечетких множеств в системе Scilab……… | 2 |
| 3. | Основы работы в Scilab………………………………………………………………… | 8 |
| 4. | Задание для лабораторной работы.................................................................................. | 11 |
| 5. | Структура отчета.............................................................................................................. | 11 |
| 6 | Исходные данные……………………………………………………………………… | 12 |
| 7. | Литература........................................................................................................................ | 12 |
Введение
Лабораторная работа выполняется на основе теории нечетких множеств на ПК с использованием систем Scilab и Microsoft WORD в среде Windows ХР/7/8/10.
Цели работы:
ознакомиться с основными логическими операциями над нечеткими множествами;
|
|
|
изучить методы построения нечетких множеств с использованием различных типов функций принадлежности;
получение умений и навыков:
построения нечетких множеств с использованием различных типов функций принадлежности с помощью пакета SciFLT системы Scilab;
выполнение основных логических операций над нечеткими множествами с помощью пакета SciFLT системы Scilab;
в анализе полученных результатов.
Построение функций принадлежности нечетких множеств в системе Scilab
Приложения Scilab позволяют работать с нечеткими множествами и нейронными сетями. Для работы с fuzzy logic нужно загрузить модуль SciFLT (FLT - fuzzy logic toolbox) в среду SciLAB. Сделать это можно открыв файл loader.sce из этого пакета и выполнив команду execute-> load into SciLAB.
Инструментарий нечеткой логики (НЛ) в составе пакета SciFLT содержит 11 встроенных типов функций принадлежности (ФП), формируемых на основе кусочно-линейных функций, распределения Гаусса, сигмоидной кривой, квадратических и кубических полиномиальных кривых. К наиболее простым ФП (и в этом их главное достоинство) можно отнести треугольную и трапециевидную. Наименование треугольной ФП – trimf (triangle membership function). В параметрическом виде она представляет собой ни что иное, как набор трех точек, образующих треугольник.
|
|
|
Описание функции: y = trimf(x, [a b c]).
Вектор x обозначает базовое множество, на котором определяется ФП. Величины a и c задают основание треугольника, b – его вершину.
В аналитическом виде треугольная ФП может быть задана следующим образом (рис. 1):
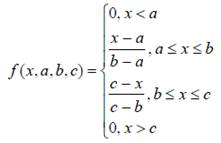
Рассмотрим примеры использования различных ФП в системе SciFLT. Примеры представляют собой фрагменты программ и комментариев на языке пакета SCILAB.
Пример 1. Программа использования ФП trimf (результат на рис.1)
x=linspace(0,1,100)'; //задаем множество х
y1=trimf(x,[0 0.2 0.4]); //и три треугольных функции на нем
y2=trimf(x,[0.2 0.5 0.9]);
y3=trimf(x,[0.5 0.6 0.9]);
xbasc();
//строим функции принадлежности
plot2d(x,[y1 y2 y3],leg="y1@y2@y3");
//подписываем рисунок
xtitle("Triangular Member Function Example","x","mu(x)");

Рис. 1. Треугольные функции
Описание функции: linspace(x1,x2,n)формирует вектор-строку из n (по умолчанию n=100) равномерно распределенных точек между x1 и x2. Символ “ ' ” в строке определения базового множества x показывает транспонированность базового множества.
Трапециевидная ФП, trapmf (trapezoid membership function), отличается от предыдущей функции лишь тем, что имеет верхнее основание.
Описание функции: y = trаpmf(x, [a b c d]), где параметры a и d задают нижнее основание, b и c – верхнее основание трапеции (рис. 2).
|
|
|
Аналитическая запись трапециевидной функции имеет вид:

Пример 2. Программа использования ФП trapmf (результат на рис. 2)
x=linspace(0,1,100)';
y1=trapmf(x,[0 0.2 0.4 0.6]);
y2=trapmf(x,[0.2 0.5 0.6 0.9]);
y3=trapmf(x,[0.5 0.6 0.8 0.9 ]);
xbasc(); plot2d(x,[y1 y2 y3],leg="y1@y2@y3");
xtitle("Trapezoidal Member Function Example","x","mu(x)");

Рис.2. Трапециедальные функции принадлежности
На основе функции распределения Гаусса в SciFLT можно построить ФП двух видов: простую ФП Гаусса и двухстороннюю ФП, образованную с помощью различных функций распределения Гаусса. Первая из них обозначается – gaussmf, а вторая – gauss2mf.
Описание функции: y = gaussmf(x, [σ c]).
Симметричная функция Гаусса зависит от двух параметров σ и с:

Описание двусторонней функции принадлежности:
y = gauss2mf(x, [σ1 c1 σ2 c2]).
Последнее выражение является комбинацией двух различных функций распределения Гаусса. Первая определяется параметрами σ1 и c1 и задает форму левой стороны, а вторая (параметры σ2 , c2 ) – правой стороны ФП.
Если c1 < c2 , то в этом случае функция gauss2mf достигает своего максимального значения на уровне 1. Иначе – максимальное значение функции меньше 1.
На рис. 3. представлены графики кривых gaussmf и gauss2mf, заданных в программе из примера 3.
|
|
|
Пример 3. Программа использования ФП gaussmf
x=linspace(0,1,100)';
y1=gaussmf(x,[0.3 0.1]);
y2=gauss2mf(x,[0.2 0.1 0.5 0.2]);
xbasc();
plot2d(x,[y1 y2],leg="y1@y2");
xtitle("Gaussian Member Function Example","x","mu(x)");
Символ “ ' ” в строке определения базового множества x показывает транспонированность базового множества.
Следующей функцией, которая позволяет представлять нечеткие субъективные предпочтения, является ФП «обобщенный колокол». Она обозначается gbellmf (bell shape membership function). Ее отличие от рассмотренных ранее ФП заключается в добавлении третьего параметра, что позволяет осуществлять плавный переход от нечеткого множества к четкому. Описание функции: y = gbellmf(x, [a b c]).

Рис. 3. Гауссовы кривые
Функция «обобщенный колокол» имеет следующий аналитический вид:

где с определяет расположение центра ФП, a и b оказывают влияние на форму кривой (рис. 4).
Пример 4. Программа использования gbellmf
x=linspace(0,1,100)';
y1=gbellmf(x,[0.5 10 0.5]);
y2=gbellmf(x,[0.2 10 0.2]);
y3=gbellmf(x,[0.7 10 0.8]);
xbasc();
plot2d(x,[y1 y2 y3],leg="y1@y2@y3");
xtitle("Generalized Bell Member Function Example","x","mu(x)");
ФП на основе функции распределения Гаусса и ФП «обобщенный колокол» отличаются гладкостью и простотой записи и являются наиболее используемыми при описании нечетких множеств. Но несмотря на то, что гауссовы и колоколообразные ФП обладают свойством гладкости, они не позволяют формировать асимметричные ФП. Для этих целей в SciFLT существует набор сигмоидных функций, которые могут быть открыты либо слева, либо справа в зависимости от типа функции. Симметричные и закрытые функции синтезируют с использованием двух дополнительных сигмоид. Основная сигмоидная ФП обозначается sigmf, а дополнительные – dsigmf и psigmf.
Описание основной сигмоидной функции: y = sigmf(x, [a c]).
В аналитической форме сигмоидная функция sigmf записывается следующим образом:

Рис. 4. Колоколообразные функции принадлежности
В зависимости от знака параметра a рассматриваемая ФП будет открыта справа или слева (рис. 5), что позволит применять ее при описании таких нечетких понятий, как «очень большой», «крайне отрицательно» и т.д.
Описание дополнительной сигмоидной функции:
y = dsigmf(x, [a1 c1 a2 c2]).
ФП dsigmf зависит от четырех параметров a1, c1, a2 и c2 и определяется как разность двух сигмоидных функций: f1(x,a1 c1), f2(x,a2 c2) .
Описание дополнительной сигмоидной функции:
y = psigmf(x, [a1 c1 a2 c2]).
ФП psigmf также как и предыдущая функция зависит от четырех параметров a1, c1, a2 и c2 и определяется как произведение двух сигмоидных функций: f1(x,a1 c1), f2(x,a2 c2).
Пример 5. Программа использования сигмоидных функций (рис.5)
x=linspace(0,1,100)';
sig1=sigmf(x,[12 0.3]);
sig2=sigmf(x,[-12 0.7]);
psig=psigmf(x,[15 0.5 -15 0.7]);
dsig=dsigmf(x,[15 0.1 15 0.3]);
xbasc();
plot2d(x,[sig1 sig2 psig dsig],leg="sig1@sig2@psig@dsig");
xtitle("Sigmoidals Member Functions Examples","x","mu(x)");
Инструментарий нечеткой логики SciFLT предоставляет возможность формирования ФП на основе полиномиальных кривых. Соответствующие функции называются Z-функции (zmf), PI-функции (pimf) и S-функции (smf).
Функция zmf представляет собой асимметричную полиномиальную кривую, открытую слева, функция smf – зеркальное отображение функции zmf. Функция pimf равна нулю в правом и левом пределах и принимает значение, равное единице в середине некоторого отрезка (рис. 6).
Описание функции: y = zmf(x, [a b]).
Параметры a и b определяют экстремальные значения кривой.
Описание функции: y = pimf(x, [a b c d]).
Параметры a и d задают переход функции в нулевое значение, параметры b и c – в единичное.
Описание функции: y = smf(x, [a b]).
Параметры a и b определяют экстремальные значения кривой.

Рис. 5. Сигмоидные функции принадлежности
Пример 6. Программа использования полиноминальных кривых (рис.6)
x=linspace(0,1,100)';
pi=pimf(x,[0.1 0.5 0.7 1.0]);
z=zmf(x,[0.2 0.4]);
s=smf(x,[0.6 0.8]);
xbasc();
plot2d(x,[pi z s],leg="pi@z@s");
xtitle("Shaped Member Functions Examples","x","mu(x)");

Рис. 6.Полиномиальные кривые
Помимо рассмотренных выше функций, позволяющих представлять нечеткие множества, в SciFLT можно формировать собственные ФП или модифицировать встроенные.
Операции с нечеткими множествами в модуле SciFLT
Выделяют три основные логические операции с нечеткими множествами: конъюнкцию, дизъюнкцию и логическое отрицание. В модуле SciFLT существует возможность определять конъюнктивные и дизъюнктивные операторы различными методами.
Коньюнкция или T-норма представляет собой нахождение логического И и представлено в программе следующими операторами:

Определение функции:
y= tnorm( x , class [,class_par]),
x – матрица, размерностью [m,n].
y – матрица, размерностью [m,1].
class – строка, задает вид T-нормы. Может принимать следующие значения: «dubois» для T-норма Дюбуа-Прада, «yager» для T-норм Ягера, «dprod» для вероятностного И, «eprod» для произведения Энштейна, «aprod» для алгебраического произведения и «min» для операции нахождения минимума;
class_par – скалярная величина, которая используется в T-нормах «dubois» и «yager».
Дизъюнкция или S-конормы представляет собой логическое ИЛИ и может быть найдена посредством следующих операторов:

Определение функции:
y=snorm( x , class [,class_par])
x – матрица, размерностью [m,n].
y – матрица, размерностью [m,1].
class – строка, задает вид S-конормы. Может принимать следующие значения: «dubois» для S-конормы Дюбуа-Прада, «yager» для S-конормы Ягера, «dsum» для вероятностного ИЛИ, «esum» для суммы Энштейна, «asum» для алгебраической суммы и «max» для операции нахождения максимума;
class_par – скалярная величина, которая используется в S-конормах «dubois» и «yager».
Пример 7. Программа использования операций min и max (рис. 7)
x=[0:0.1:10]';
y1=gaussmf(x,[3 1.2]);
y2=gaussmf(x,[7 1]);
yy1=tnorm([y1 y2],'min');
yy2=snorm([y1 y2],'max');
yy3=tnorm([y1 y2],'dprod');
yy4=snorm([y1 y2],'dsum');
xbasc();
subplot(3,1,1);
plot2d(x,[y1 y2],leg='mf1@mf2',rect=[0 -0.1 10 1.1]);
xtitle('Member Function Evaluation','x','mu(x)');
subplot(3,1,2);
plot2d(x,[yy1 yy3],leg='min@dprod',rect=[0 -0.1 10 1.1]);
xtitle('AND OPERATION','x','and(mf1,mf2)');
subplot(3,1,3);
plot2d(x,[yy2 yy4],leg='max@dsum',rect=[0 -0.1 10 1.1]);
xtitle('OR OPERATION','x','or(mf1,mf2)');
Минимаксная интерпретация является наиболее распространенной при построении нечетких систем. Тем не менее, на практике довольно часто используется альтернативная вероятностная интерпретация конъюнктивных и дизъюнктивных операторов.
Дополнение нечеткого множества есть не что иное, как математическое представление вербального выражения “НЕ A”, где A – нечеткое множество, описывающее некоторое размытое суждение.
Описание функции дополнения:
y=complement( x , class [,class_par]),
где x, у – матрицы, размерностью [m,n].
class – строка, задает вид оператора дополнения. Может принимать следующие значения: «one» для обычного дополнения, «sugeno» для дополнения по формуле Сугено и «yager» для формулы Ягера;
class_par – скалярная величина, которая используется в S-конормах «sugeno» и «yager».
Математическая запись функций дополнения следующая:

Пример 8. Программа использования операции дополнения (рис. 8)
x=[0:0.1:10]';
y1=gaussmf(x,[3 1.2]);
y2=complement(y1,’one’);
xbasc();
plot2d(x,[y1 y2],leg='mf1@Not_mf1',rect=[0 -0.1 10 1.1]);
xtitle('Member Function and Inverse','x','mu(x)');

Рис. 7. Результаты работы программы из примера 7
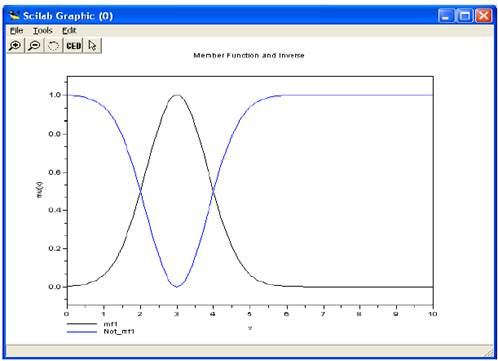
Рис.8. Функция дополнения
Дата добавления: 2019-09-13; просмотров: 1485; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
