Подставляя величины деформации и напряжения из уравнений (1.17, 1.18) в уравнение (1.24), получаем следующее уравнение
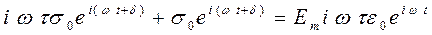 (1.25)
(1.25)
из которого следует, что
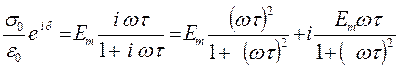 . (1.26)
. (1.26)
После подстановки величины 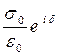 из уравнения (1.21), получим
из уравнения (1.21), получим
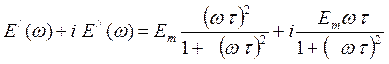 , (1.27)
, (1.27)
То есть 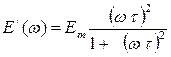 ,
, 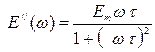 ,
, 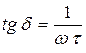 . (1.28)
. (1.28)
Для обобщенной модели Максвелла, приведенной на рис.1.2 д, с дискретным набором времен релаксации 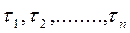 получим
получим
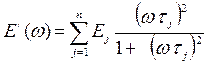 , (1.29)
, (1.29)
 , (1.30)
, (1.30)
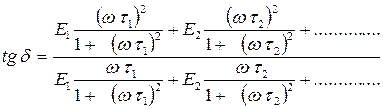 . (1.31)
. (1.31)
Для решения задач динамики упругопластических тел под пластическими деформациями понимаются микропластические деформации [6]. Эти деформации имеют место при любом уровне напряжений, в этом числе и при напряжениях, меньших макроскопического предела текучести материала
Будем рассматривать только одномерный вариант теории, основанный на использовании одномерных реологических моделей для описания простейших эффектов амплитудно-зависимого внутреннего трения.
Простейшая реологическая обобщенная модель Прандтля для упругопластического материала приведена на рис. 1.6. Она представляет собой последовательное соединение пружин жесткости 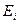 и элементов сухого трения (элемент Сен-Венана) с безразмерным пределом текучести
и элементов сухого трения (элемент Сен-Венана) с безразмерным пределом текучести 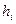 . Отношение напряжение - деформация для модели Прандтля имеет вид [7]
. Отношение напряжение - деформация для модели Прандтля имеет вид [7]
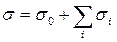 , (1.32)
, (1.32)
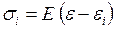 , (1.33)
, (1.33)
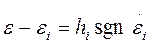 (1.34)
(1.34)
|
|
|
где 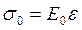 ,
,
где 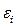 – пластическая деформация элемента сухого трения.
– пластическая деформация элемента сухого трения.
Рассмотрим поведение материала при гармоническом законе деформирования во времени
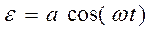 , (1.35)
, (1.35)
где 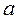 – амплитуда деформации, а
– амплитуда деформации, а 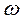 – частота,
– частота, 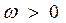 .
.
Практический интерес представляет знание той же гармонической зависимости для напряжения. Чтобы ее найти, воспользуемся методом
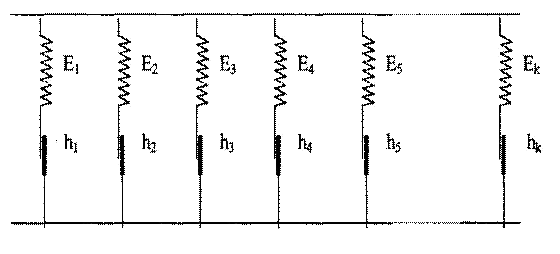
Рис.1.6. Обобщенная модель Прандтля
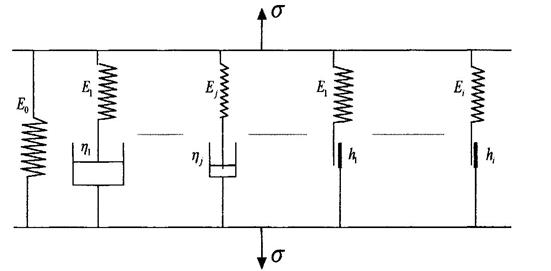
Рис.1.7. Упруговязкопластическая модель
гармонической линеаризации [28]. В соответствии с этим методом положим, что пластическая деформация 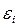 в каждом элементе также изменяется во времени по гармоническому закону, и проведем гармоническую линеаризацию единственной нелинейной функции в соотношении (1.34)
в каждом элементе также изменяется во времени по гармоническому закону, и проведем гармоническую линеаризацию единственной нелинейной функции в соотношении (1.34)
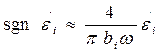 , (1.36)
, (1.36)
где 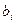 - амплитудное значение деформации
- амплитудное значение деформации 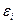 .
.
В результате линеаризации нелинейное уравнение (1.34) преобразуется к следующему виду
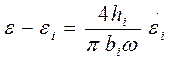 . (1.37)
. (1.37)
Линейность уравнения (1.37) позволяет использовать в дальнейшем комплексную форму записи переменных
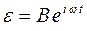 ,
, 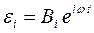 , (1.38)
, (1.38)
где 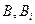 - комплексные величины.
- комплексные величины.
|
|
|
Подставляя (1.38) в (1.37), получим
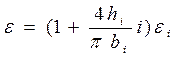 . (1.39)
. (1.39)
Амплитуда полной деформации 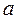 и введенная ранее амплитуда пластической деформации
и введенная ранее амплитуда пластической деформации 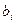 следующим образом выражаются через комплексные значения переменных
следующим образом выражаются через комплексные значения переменных 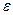 и
и 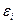
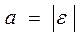 ,
, 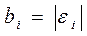 . (1.40)
. (1.40)
Подставляя (1.40) в (1.39), получим
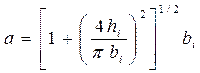 . (1.41)
. (1.41)
Отсюда легко находим
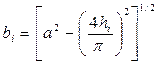 . (1.42)
. (1.42)
Это выражение имеет смысл только при 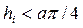 , в противном случае оно теряет смысл. Подставляя (1.42) в (1.37), получим
, в противном случае оно теряет смысл. Подставляя (1.42) в (1.37), получим
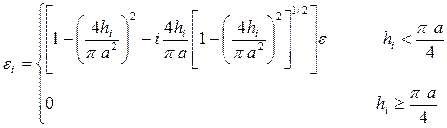 . (1.43)
. (1.43)
После подстановки величин 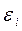 из уравнения (1.43) в уравнение (1.32), получим
из уравнения (1.43) в уравнение (1.32), получим
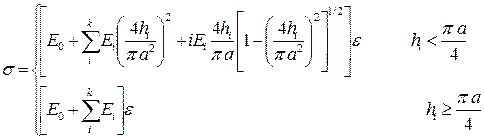 . (1.44)
. (1.44)
Тогда комплексный модуль равен
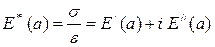 . (1.45)
. (1.45)
Могут быть получены также амплитудные зависимости динамического модуля. При подстановке (1.44) в (1.45), получим
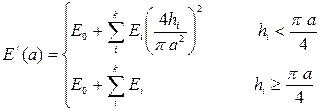 , (1.46)
, (1.46)
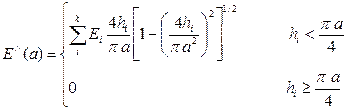 . (1.47)
. (1.47)
Порознь все эти проявления зафиксированы экспериментально, однако адекватно описывающая их общая модель материала еще далека от совершенства. Наиболее полно современным представлениям о структуре и поведении резины соответствует обобщенная модель Максвелла (параллельное соединение упруго-вязких звеньев) с добавлением в параллель упруго-пластических звеньев (см. рис.1.7).
|
|
|
Сравнение вышеописанных теоретически полученных результатов для динамического модуля 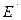 и
и 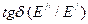 , определенных расчетным путем из уравнений (1.46), (1.47) и этих величин, полученных экспериментально, показали, что для приведенных моделей погрешность определения динамического модуля достигает 20% в сравнении с экспериментальными кривыми [31,32]. Кроме того, различаются сами формы зависимости
, определенных расчетным путем из уравнений (1.46), (1.47) и этих величин, полученных экспериментально, показали, что для приведенных моделей погрешность определения динамического модуля достигает 20% в сравнении с экспериментальными кривыми [31,32]. Кроме того, различаются сами формы зависимости 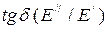 , определенной из уравнений (1.46), (1.47), и этой зависимости, полученной экспериментально. Получаемые расчетным путем зависимости были негладкими, со скачками в точках около значений дискретных пределов текучести и, следовательно, со значительными отклонениями от экспериментальных кривых.
, определенной из уравнений (1.46), (1.47), и этой зависимости, полученной экспериментально. Получаемые расчетным путем зависимости были негладкими, со скачками в точках около значений дискретных пределов текучести и, следовательно, со значительными отклонениями от экспериментальных кривых.
Таким образом, наилучшим вариантом является экспериментальное определение для эластомеров нагрузочных кривых растяжения и сжатия, кривых релаксации и ползучести, динамических модулей и модулей внутреннего трения в возможно более широком диапазоне частот и температур.
Упруговязкопластическую (тиксотропную) модель эластомеров, рассмотренную выше, следует использовать при расчетах с использованием МКЭ для интерпретации результатов и экстраполяции за пределы экспериментального диапазона.
|
|
|
При расчетах с использованием МКЭ необходимо также учитывать коэффициенты трения и интенсивности изнашивания эластомеров, а также возможность их разрушения при резком перепаде давлений (явление взрывной декомпрессии). Трибологические свойства эластомеров и их устойчивость к взрывной декомпрессии вообще может быть определена только экспериментальным путем.
Дата добавления: 2019-09-13; просмотров: 280; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
