В каких случаях производят расчет валов на жесткость?
8.11. Для расчета валов и осей на прочность и жесткость составляют расчетную схему. При расчете на изгиб вращающиеся валы и оси рассматривают как балки на шарнирных опорах. На расчетных схемах силы и вращающие моменты условно принимают как сосредоточенные.
Влияние силы тяжести валов (и деталей), силы трения в опорах не учитывают.
Как изображают силы на расчетньа схемах па длине ступицы?
Лекция 3.21 Самостоятельно.
Расчет осей на статическую прочность
Как указывалось выше, оси не испытывают кручения, поэтому их рассчитывают только на изгиб.
8.12. Последовательность проектировочного расчета.
По конструкции узла (рис. 8.8, а) составляют расчетную схему (рис. 8.8, б), определяют силы, действующие на ось, строят эпюры изгибающих моментов; диаметр оси определяют по формуле
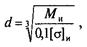(8.2)
где Ми — максимальный изгибающий момент; [σ]и — допускаемое напряжение изгиба.
Выбор [σ]и.
Во вращающихся осях напряжение изгиба изменяется по симметричному циклу: для них принимают 
, в неподвижных 
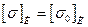. Для вращающихся осей из Ст5 [σ]и = 50 ÷ 80 МПа, для невра- вдающихся [σ]и = 100 ÷ 160 МПа (меньшие значения рекомендуется принимать при наличии концентраторов напряжений).
Рис. 8.8. Расчетная схема оси: а — конструкция; б — расчетная схема; в — эпюра изгибающих моментов
Полученное значение диаметра оси d округляют до ближайшего большего стандартного размера:
|
|
|
16, 17, 18, 19; 20; 21; 22; 23; 24;
25; 26; 28; 30; 32; 34; 36; 38; 40;
42; 45; 48; 50; 52; 55; 60; 63; 65;
70; 75; 80; 85; 90; 95; 100.
Если ось в расчетном сечении имеет шпоночную канавку, то ее диаметр увеличивают на 10 %.
8.13. Проверочный расчет осей на статическую прочность.
Этот расчет производят по формуле
(8.3)
где а„ — расчетное напряжение изгиба в опасном сечении оси.
Испытывают ли оси деформацию кручения?
§ 4. Приближенный расчет валов на прочность
При этом методе расчета различие характера циклов изменения нормальных и касательных напряжений и их влияние на прочность не учитывают.
В зависимости от действия нагрузок возможны два случая приближенного расчета валов на прочность: расчет только на кручение и расчет на совместное действие кручения и изгиба.
Приближенный расчет выполняют как проектировочный, на основе которого ориентировочно устанавливают диаметры характерных сечений вала (методика изложена в шаге 8.14 или 8.15) с последующим уточнением коэффициентов запаса прочности по выносливости (уточненный расчет см. § 5).
8.14. Расчет валов на кручение.
При этом расчете обычно определяют диаметр выходного конца вала или диаметр вала под подшипником (под опорой), который испытывает только кручение.
|
|
|
Исходя из условия прочности (8.1) выполняют проектировочный расчет
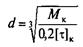(8.4)
и проверочный расчет
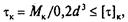(8.5)
где d — расчетный диаметр вала; Мк — крутящий момент в опасном сечении вала; τк и [τ]к — расчетное и допускаемое напряжения кручения в опасном сечении вала (для сталей 45 и Ст5 [τ]к = 25 ÷ 35 МПа).
Назовите участки вала, которые рассчитывают по формуле (8.4).
8.15. Расчет валов на совместное действие кручения и изгиба.
Участок вала между опорами (под шестерней, колесом и т. п.) рассчитывают на совместное действие кручения и изгиба по эквивалентному моменту Мэкв.
Эквивалентный момент вычисляют обычно по формуле (при расчете по теории максимальных касательных напряжений):
(8.6)
где Ми и Мк — изгибающий и крутящий моменты.
По аналогии с рассмотренными в шагах 8.12—8.14 случаями расчета выполняют:
проектировочный расчет
(8.7)
|
|
|
и проверочный расчет
(8.8)
где σэкв — эквивалентное напряжение для расчетного сечения вала.
Получив расчетным путем размеры, с учетом технологии изготовления проектируют конструктивную форму вала.
Приближенный расчет на совместное действие кручения и изгиба для неответственных конструкций валов можно считать основным. Уточненный расчет на выносливость (см. § 5) можно не производить, если соблюдается условие
(8.8а)
где σ-1, — предел выносливости материала при изгибе (симметричный цикл); Kd — масштабный коэффициент; Кп — эффективный коэффициент концентрации напряжений в опасном сечении; [ s ] — допускаемый коэффициент запаса прочности по выносливости; Kd , Ka , [ s ] — устанавливаются в шагах 8.17—8.18.
Когда применяют метод расчета валов, изложенный в шаге 8.15? Чем отличаются расчеты по формулам (8.7), (8.8) и (8.2), (8.3)?
8.16. Порядок приближенного (проектировочного) расчета валов на прочность по Мэкв:
1. По чертежу узла составляют расчетную схему (рис. 8.9, а).
2. Определяют действующие на вал силы; если они действуют не в одной плоскости, то их необходимо разложить по двум взаимно перпендикулярным плоскостям. При угле между плоскостями менее 30° все силы можно рассматривать как действующие в одной плоскости.
|
|
|
В схеме (см. рис. 8.9, а) Мк — крутящий момент, возникающий в поперечных сечениях вала; FB и FT — силы, действующие на вал в вертикальной и в горизонтальной плоскостях.
|
|
Рис. 8.9. Расчетная схема валов: а — схема нагружения; б — эпюра изгибающего момента в
вертикальной плоскости; в — эпюра изгибающего момента в горизонтальной плоскости; г —
эпюра крутящего момента; д — эскиз вала
3. Определяют опорные реакции:
в вертикальной плоскости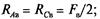 
в горизонтальной плоскости 
.
4. Изгибающие моменты Ми и их эпюры:
в вертикальной плоскости — в сечении Аи С МИ В = 0;
в сечении В 
(рис. 8.9, б);
в горизонтальной плоскости — в сечении А и С Миг= 0;
в сечении В 
(рис. 8.9, в).
5. Суммарный изгибающий момент в сечении В
(8.9)
6. Определяют крутящий момент и строят эпюру (см. рис. 8.9, г):
(8.10)
где Р — мощность, Вт; со — угловая скорость, рад/с.
7. По формуле (8.6) определяют эквивалентный момент, диаметр вала между опорами определяют по формуле
(8.7):
Полученное значение d округляют до ближайшего большего стандартного (см. шаг 8.12).
8. Определяют диаметры под подшипниками don (рис. 8.9, д) и округляют до большего стандартного значения.
Как определить диаметр вала don под опорой С для схемы нагрузки вала, показанной на рис. 8.9, а?
Дата добавления: 2019-09-13; просмотров: 625; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!