Модифицированный метод Эйлера с пересчетом

Содержание

 

ВВЕДЕНИЕ

1. ПОСТАНОВКА ЗАДАЧИ

2. ОБЗОР ЛИТЕРАТУРЫ

2.1 Методы решения

2.2 Общая постановка задачи решения ОДУ

3. ПРОЕКТИРОВАНИЕ МАТЕМАТИЧЕСКОГО ОБЕСПЕЧЕНИЯ

3.1.0 Математический метод решения задачи методом Рунге-Кутты

3.1.1 Блок-схема метода Рунге-Кутты

3.1.2 Анализ погрешности метода Рунге-Кутты

3.1.3 Достоинства и недостатки метода Рунге-Кутты

3.1.4 Математический метод решения задачи модифицированным методом Эйлера

3.1.5 Блок-схема модифицированного метода Эйлера

3.1.6 Анализ погрешности модифицированного метода Эйлера

3.2 Архитектура разрабатываемых програмних средств

3.3 Требования к программному изделию

4. РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ

5. ЭКСПЕРИМЕНТАЛЬНЫЕ РАСЧЕТЫ

ЗАКЛЮЧЕНИЕ

ЛИТЕРАТУРА

ПРИЛОЖЕНИЕ

 

ВВЕДЕНИЕ

 

Дифференциальные уравнения - это уравнения, в которых неизвестными являются не переменные (т. е. числа), а функции одной или нескольких переменных. Эти уравнения (или системы) включают соотношения между искомыми функциями и их производными. Если в уравнения входят производные только по одной переменной, то они называются обыкновенными дифференциальными уравнениями (ОДУ). В противном случае говорят об уравнениях в частных производных. Таким образом, решить дифференциальное уравнение - значит определить неизвестную функцию на определенном интервале изменения ее переменных.

Как известно, одно обыкновенное дифференциальное уравнение или система ОДУ имеет единственное решение, если помимо уравнения определенным образом заданы начальные или граничные условия. В соответствующих курсах высшей математики доказываются теоремы о существовании и единственности решения в зависимости от тех или иных условий. Имеются два типа задач:

1. задачи Коши - для которых определены начальные условия на искомые функции, т. е. заданы значения этих функций в начальной точке интервала интегрирования уравнения;

2. краевые задачи - для которых заданы определенные соотношения сразу на обеих границах интервала.

Как правило, решение задач Коши для ОДУ - задача, хорошо разработанная и с вычислительной точки зрения не слишком сложная. Большое значение здесь имеет представление результатов и анализ зависимостей решения от различных параметров системы.

В данной работе рассматривается один из способов решение дифференциальных уравнений – метод Адамса.

 

1. ПОСТАНОВКА ЗАДАЧИ

 

Целью данного проекта есть реализация решения ОДУ 2-го порядка вида x”=-4x’ методом Рунге-Кутты, модифицированным методом Эйлера и построение на ЭВМ системы отображения результатов в табличной форме и в виде графика.

Разрабатываемая программа должна выполнять следующие функции:

1) Ввод пользователем данных.

2) Построение на их основе дифференциального уравнения.

3) Проведение анализа такой модели на адекватность, построение графика.

4) Анализ результатов.

5) Вывод полученных результатов на экран.

2. ОБЗОР ЛИТЕРАТУРЫ

 

2.1 Методы решения

 

Дифференциальные уравнения являются основным математическим инструментом моделирования и анализа разнообразных явлений и процессов в науке и технике.

Методы их решения подразделяются на два класса:

1) аналитические методы, в которых решение получается в виде аналитических функций;

2) численные (приближенные) методы, где искомые интегральные кривые получают в виде таблиц их численных значений.

Применение аналитических методов позволяет исследовать полученные решения методами математического анализа и сделать соответствующие выводы о свойствах моделируемого явления или процесса. К сожалению, с помощью таких методов можно решать достаточно ограниченный круг реальных задач. Численные методы позволяют получить с определенной точностью приближенное решение практически любой задачи. В работе рассмотрен два из численных методов решения дифференциального уравнения - метод Рунге-Кутта и модифицированный метод Эйлера.

 

2.2 Общая постановка задачи решения обыкновенных дифференциальных уравнений

 

Обыкновенными дифференциальными уравнениями описывают задачи движения системы взаимодействующих материальных точек, сопротивление материалов и многое другое. Ряд важных задач для уравнений в частных производных также сводятся к задачам для обыкновенных дифференциальных уравнений. Таким образом, решение обыкновенных дифференциальных уравнений занимает важное место среди прикладных задач физики, химии, техники.

Конкретная прикладная задача может приводить к дифференциальному уравнению любого порядка или системе уравнений любого порядка. Однако обыкновенные дифференциальные уравнения n-го порядка можно с помощью замены свести к эквивалентной системе n уравнений первого порядка.

Различают три основных типа задач для решения обыкновенных дифференциальных уравнений: задачи Коши, краевые задачи и задачи на собственные значения. В этой курсовой работе будут рассматриваться методы решения задач Коши.

Пусть задано дифференциальное уравнение первого порядка в виде

 

 (1.1)

 

и начальное условие

 

 (1.2)

 

Задача Коши состоит в том, чтобы найти функцию

 

,

 

являющуюся решением уравнения (1.1) и удовлетворяющую условию(1.2).

Методы решения можно условно разбить на точные, приближенные и численные. К точным относятся методы, с помощью которых можно выразить решение дифференциального уравнения через элементарные функции. Приближенные методы – это методы, в которых решение получается как предел некоторой последовательности. Численные методы – это алгоритмы вычисления приближенных значений искомого решения на некоторой выбранной сетке значений аргумента. Решение при этом получается в виде таблицы.

 

3. ПРОЕКТИРОВАНИЕ МАТЕМАТИЧЕСКОГО ОБЕСПЕЧЕНИЯ

 

3.1.0 Математический метод решения задачи

 

Метод Рунге-Кутта

Метод Рунге-Кутта — важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Формально, методом Рунге — Кутты является модифицированный и исправленный метод Эйлера, они представляют собой схемы второго порядка точности. Существуют стандартные схемы третьего порядка, не получившие широкого распространения. Наиболее часто используется и реализована в различных математических пакетах (Matlab, MathCAD) стандартная схема четвёртого порядка.

Метод Рунге—Кутты 4 порядка

Рассмотрим задачу Коши

 

 

Тогда приближенное значение в последующих точках вычисляется по итерационной формуле:

 

 

где h — величина шага сетки по x и вычисление нового значения проходит в четыре стадии:

 

 

Этот метод имеет четвёртый порядок точности, т.е. суммарная ошибка на конечном интервале интегрирования имеет порядок O(h⁴) (ошибка на каждом шаге порядка O(h⁵)) [1].

 

3.1.1 Блок схема метода Рунге-Кутты

 

 

3.1.2 Анализ погрешности метода Рунге-Кутты

Из теории приближенных методов известно, что при шаге интегрирования h имеет место оценка

 

,

 

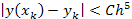так что погрешность одного шага вычислений имеет порядок . Суммарная погрешность за n шагов будет порядка . Отсюда, если увеличить n в два раза. То погрешность уменьшиться примерно в 16 раз. Поэтому для оценки приближенного решения 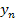, полученного с шагом h, повторяют вычисление с шагом 2h и за абсолютную погрешность принимают число

 

,

 

где  - приближенное решение с шагом 2h.

Приведенная оценка является оценкой метода и не учитывает погрешность при округлении.[2]

 

3.1.3Достоинства и недостатки метода Рунге-Кутты

Методы Рунге-Кутта обладают следующими отличительными свойствами:

* Эти методы одноступенчатые: чтобы найти y[m+1], нужна информация только о предыдущей точке x[m],y[m].

* Они согласуются с рядом Тейлора вплоть до членов порядка h^p,

где p - различна для разных методов и называется порядком метода.

* Они не требуют вычисления производных от f(x,y), а требуют только вычисления самой функции.

Именно благодаря 3) эти методы удобны для практических вычислений, однако для вычисления одной последующей точки решения нам придется вычислять f(x,y) несколько раз при различных x и y.

 

3.1.4Модифицированный метод Эйлера:

Метод Эйлера — наиболее простой численный метод решения (систем) обыкновенных дифференциальных уравнений. Впервые описан Леонардом Эйлером в 1768 году в работе «Интегральное исчисление»^[1]. Метод Эйлера является явным, одношаговым методом первого порядка точности, основанном на аппроксимации интегральной кривой кусочно линейной функцией, т. н. ломаной Эйлера.

Описание метода

Пусть дана задача Коши для уравнения первого порядка

где функция определена на некоторой области . Решение разыскивается на интервале . На этом интервале введем узлы

Приближенное решение в узлах , которое обозначим через определяется по формуле

Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.

 

Модифицированный метод Эйлера с пересчетом

Вычисления по методу Эйлера с пересчетом делаются в два этапа.

Прогноз:

.

Коррекция:

.

Модифицированный метод Эйлера с пересчетом имеет второй порядок точности, однако для его реализации необходимо дважды вычислять правую часть функции. Заметим, что метод Эйлера с пересчетом представляет собой разновидность методов Рунге-Кутты .

 

3.1.5 Блок схема модифицированного метода Эйлера.

 3.1.6 Анализ погрешности модифицированного метода

Метод Эйлера является методом первого порядка. Если функция непрерывна в и непрерывно дифференцируема по переменной в , то имеет место следующая оценка погрешности

где — средний шаг, то есть существует такая, что .

Заметим, что условия гладкости на правую часть, гарантирующие единственность решения задачи Коши, необходимы для обоснования сходимости метода Эйлера.

3.2 Архитектура разрабатываемых програмних средств

 

Схема взаимодействия программ

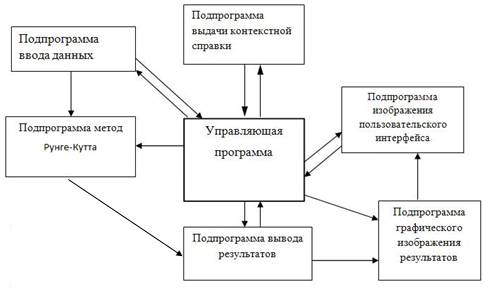
Рис1. Структурная схема программы

 

Программа представляет собой следующие функциональные блоки :

- Управляющая программа:

функции: общее управление программой;

вх.данные: команды пользователя и ОС;

вих. данные: управляющие команды другими блоками программы;

- Подпрограмма изображения пользовательского интерфейса:

функции: изображение удобных для пользователя элементов управления и руководство ими;

вх. данные: типы элементов управление, их свойства;

вых. данные: элементы управления на экране, меню;

- Подпрограмма ввода данных:

функции: ввод данных пользователем;

вх. данные: исходные данные, метод получения информации;

вых. данные: преобразование входных данных во внутренние переменные;

- Подпрограмма метод Рунге-Кутта:

функции: нахождение очередной точки

вх. данные: начальная точка, шаг, значение функции и производной в ней ;

вых. данные: масив значений производных в n точах;

- Подпрограмма вывода результатов:

функции: вывод результатов работы программы;

вх. данные: массивы значений связанных определенным отношением x и х1 отображающие результаты расчёта произвольного дифференциального уравнения 1-го или 2-го порядка методом Рунге-Кутты;

вых. данные: результаты работы программы на экране;

- Подпрограмма графического представления результатов

 

- Подпрограмма модифицированный метод Эйлера:

функции: нахождение очередной точки

вх. данные: начальная точка, шаг, значение функции и производной в ней ;

вых. данные: масив значений производных n точках;

- Подпрограмма вывода результатов:

функции: вывод результатов работы программы;

вх. данные: массивы значений связанных определенным отношением x и х1 отображающие результаты расчёта произвольного дифференциального уравнения 1-го или 2-го порядка модифицированным методом Эйлера;

вых. данные: результаты работы программы на экране;

- Подпрограмма графического представления результатов

 

 

Перечень программных документов:

· Техническое задание;

· Пояснительная записка;

· Текст задания на языке програмирования Delphi.

 

4. РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ

---

Дата добавления: 2019-09-02; просмотров: 1061; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!