Замена переменной под знаком определенного интеграла.
Пусть выполнены следующие условия:
1) функция 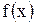 непрерывна на сегменте
непрерывна на сегменте 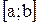 ;
;
2) сегмент 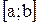 является множеством значений некоторой функции
является множеством значений некоторой функции 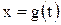 , определенной на сегменте
, определенной на сегменте 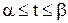 и имеющей на этом сегменте непрерывную производную;
и имеющей на этом сегменте непрерывную производную;
3) 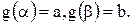
При этих условиях справедлива формула
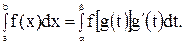 (4)
(4)
Формула (4) показывает, что если вычислен интеграл, стоящий в левой части этой формулы, то также вычислен интеграл, стоящий в правой части, и наоборот. Указанная формула называется формулой замены переменной под знаком определенного интеграла.
Рассмотрим некоторую первообразную 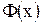 функции
функции 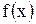 . По формуле (2) имеем
. По формуле (2) имеем
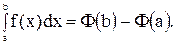 (5)
(5)
Так как функции 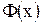 и
и 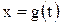 дифференцируемы на соответствующих сегментах, то сложная функция
дифференцируемы на соответствующих сегментах, то сложная функция 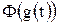 дифференцируема на сегменте
дифференцируема на сегменте 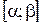 . Поэтому, применяя правило дифференцирования сложной функции, получим
. Поэтому, применяя правило дифференцирования сложной функции, получим
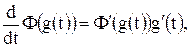 (6)
(6)
причем производная 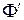 вычисляется по аргументу х:
вычисляется по аргументу х: 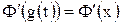 , где
, где 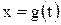 . Поскольку
. Поскольку 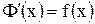 , то при
, то при 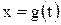 получим
получим 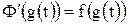 . Подставляя это значение
. Подставляя это значение 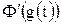 в правую часть равенства (6), получим
в правую часть равенства (6), получим
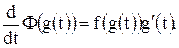
Следовательно, функция 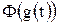 , определенная на сегменте
, определенная на сегменте 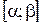 , является на этом сегменте первообразной для функции
, является на этом сегменте первообразной для функции 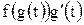 , и поэтому, согласно формуле (2),
, и поэтому, согласно формуле (2),
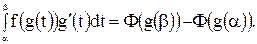
Так как 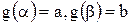 , то
, то
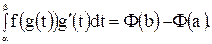
Сравнивая последнюю формулу с формулой (5), мы убеждаемся в справедливости формулы (4).
|
|
|
Отметим, что:
1) при вычислении определённого интеграла методом подстановки возвращаться к старой переменной не требуется;
2) часто вместо подстановки 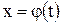 применяют подстановку
применяют подстановку 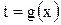 ;
;
3) не следует забывать менять пределы интегрирования при замене переменных.
Пример 1.
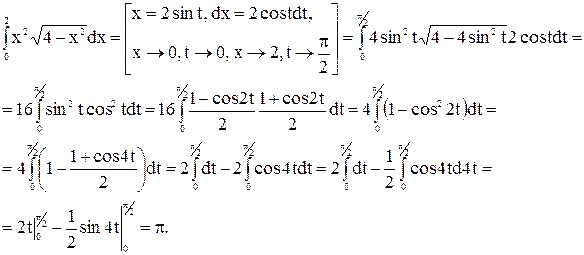
Формула интегрирования по частям.
Пусть функций 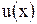 и
и 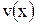 имеют непрерывные производные на сегменте
имеют непрерывные производные на сегменте 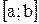 . Тогда имеет место следующая формула интегрирования по частям определенных интегралов:
. Тогда имеет место следующая формула интегрирования по частям определенных интегралов:
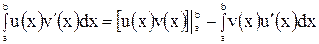 . (7)
. (7)
Так как 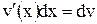 и
и 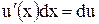 , то эту формулу записывают еще следующим образом:
, то эту формулу записывают еще следующим образом:
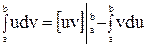 . (8)
. (8)
В справедливости этих формул убедиться нетрудно. Действительно, функция 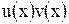 является первообразной для функции
является первообразной для функции 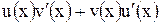 . Поэтому
. Поэтому
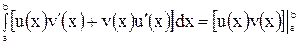 .
.
Отсюда, используя свойства определенных интегралов, мы и получим формулы (7) и (8).
Пример 2.
1) 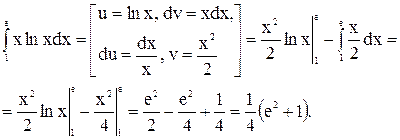
2) 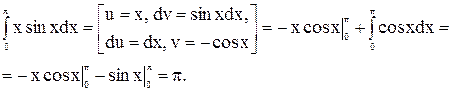
Геометрические и физические приложения
Определённого интеграла.
Площадь плоской фигуры.
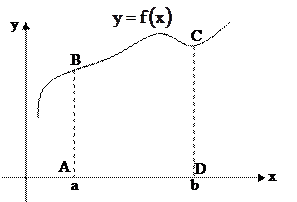 Площадь криволинейной трапеции ABCD, ограниченной сверху графиком функции
Площадь криволинейной трапеции ABCD, ограниченной сверху графиком функции 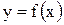 , слева и справа - прямыми
, слева и справа - прямыми 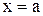 и
и 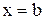 соответственно, снизу - осью Ох, вычисляется по формуле
соответственно, снизу - осью Ох, вычисляется по формуле
|
|
|
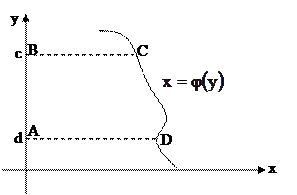
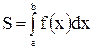 .
.
Площадь криволинейной трапеции ABCD, ограниченной справа графиком функции 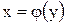 , сверху и снизу - соответственно прямыми
, сверху и снизу - соответственно прямыми 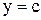 ,
, 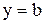 , слева - осью Оу, определяется формулой
, слева - осью Оу, определяется формулой
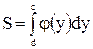 .
.
 Если функция
Если функция 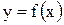 - не положительна на отрезке
- не положительна на отрезке 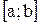 , то площадь S над кривой
, то площадь S над кривой 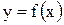 на
на 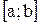 равна определённому интегралу от
равна определённому интегралу от 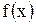 на
на 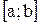 , взятому со знаком «минус»:
, взятому со знаком «минус»: 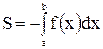 .
.
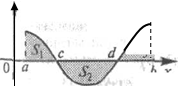
Пусть на отрезке 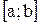 задана непрерывная функция
задана непрерывная функция 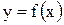 общего вида. Предположим также, что исходный отрезок можно разбить точками на конечное число интервалов так, что на каждом из них функция
общего вида. Предположим также, что исходный отрезок можно разбить точками на конечное число интервалов так, что на каждом из них функция 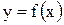 будет знакопостоянна или равна нулю. Площадь заштрихованной фигуры
будет знакопостоянна или равна нулю. Площадь заштрихованной фигуры 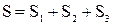 , т.е. равна алгебраической сумме соответствующих определенных интегралов:
, т.е. равна алгебраической сумме соответствующих определенных интегралов: 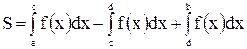 .
.
Теорема 1. Пусть на отрезке 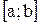 заданы непрерывные функции
заданы непрерывные функции 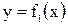 и
и 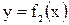 такие, что
такие, что 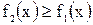 . Тогда площадь S фигуры, заключенной между кривыми
. Тогда площадь S фигуры, заключенной между кривыми 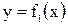 и
и 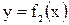 , на отрезке
, на отрезке 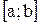 вычисляется по формуле
вычисляется по формуле 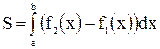 .
.
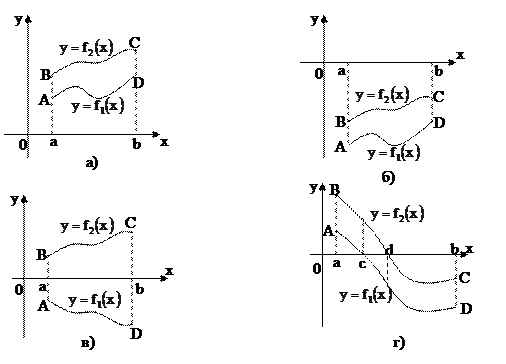 |
Проиллюстрируем теорему графически. Возможны несколько случаев расположения кривых на отрезке 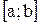 .
.
1. 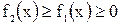 , рис. а.
, рис. а.
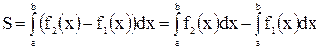 .
.
2. 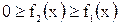 , рис. б.
, рис. б.
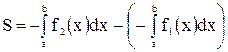 .
.
3. 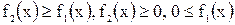 , рис. в.
, рис. в.
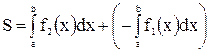 .
.
4. Общий случай (рис. г) сводится к частным случаям, рассмотренным выше, если разбить отрезок 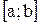 на отдельные отрезки
на отдельные отрезки 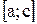 ,
, 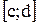 ,
, 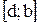 .
.
Если криволинейная трапеция ограничена кривой, заданной параметрически
|
|
|
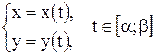 ,
,
прямыми 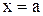 и
и 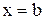 и осью Ох, то площадь ее находится по формуле
и осью Ох, то площадь ее находится по формуле 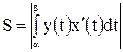 , где
, где 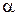 и
и 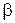 определяются из равенств
определяются из равенств 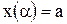 и
и 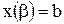 .
.
Пример 3. Вычислить площадь фигуры, ограниченной эллипсом 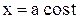 ,
, 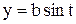 .
.
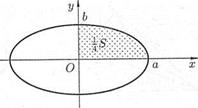 Найдем сначала
Найдем сначала 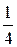 площади S. Здесь х изменяется от 0 до а, следовательно, t изменяется от
площади S. Здесь х изменяется от 0 до а, следовательно, t изменяется от 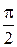 до 0. Находим:
до 0. Находим:
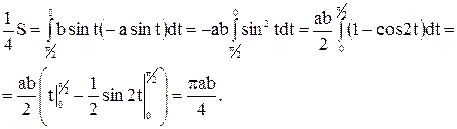
Значит, 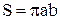 .
.
Найдем площадь S криволинейного сектора, т. е. плоской фигуры, ограниченной непрерывной линией 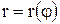 и двумя лучами
и двумя лучами 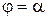 и
и 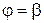
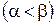 , где
, где 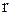 и
и 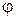 - полярные координаты. Искомая площадь равна
- полярные координаты. Искомая площадь равна 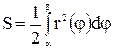 .
.
Пример 4. Найти площадь фигуры, ограниченной «трехлепестковой розой» 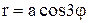 .
.
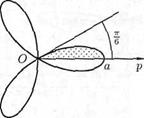 Найдем сначала площадь половины одного лепестка «розы», т. е.
Найдем сначала площадь половины одного лепестка «розы», т. е. 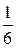 часть всей площади фигуры:
часть всей площади фигуры:
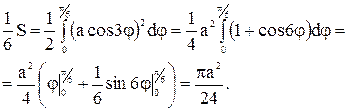
Следовательно, 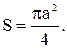
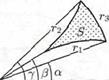
Если плоская фигура имеет «сложную» форму, то лучами, выходящими из полюса, ее следует разбить на криволинейные секторы, к которым применить полученную формулу для нахождения площади. Так, для фигуры, изображенной на рисунке, имеем:
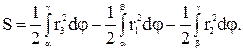
Дата добавления: 2019-09-02; просмотров: 516; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
