Основные правила интегрирования.
Существование первообразной
Для непрерывной функции.
Прежде чем перейти к доказательству теоремы о существовании первообразной для непрерывной функции, введем понятие интеграла с переменным верхним пределом.
Пусть функция  интегрируема на любом сегменте, содержащемся в интервале
интегрируема на любом сегменте, содержащемся в интервале  , и пусть с - некоторая фиксированная точка этого интервала. Тогда, каково бы ни было число х из интервала
, и пусть с - некоторая фиксированная точка этого интервала. Тогда, каково бы ни было число х из интервала  , функция
, функция  интегрируема на сегменте
интегрируема на сегменте  . Поэтому на интервале
. Поэтому на интервале  определена функция
определена функция

которую называют интегралом с переменным верхним пределом.
Теорема 1. Любая непрерывная на интервале  функция
функция  имеет на этом интервале первообразную. Одной из первообразных является функция
имеет на этом интервале первообразную. Одной из первообразных является функция

где с - любая фиксированная точка интервала  .
.
Доказательство. Достаточно доказать, что для любого фиксированного х из интервала  существует предельное значение
существует предельное значение  , причем это предельное значение равно
, причем это предельное значение равно  . Имеем, в силу свойства 6 определенных интегралов
. Имеем, в силу свойства 6 определенных интегралов

По формуле среднего значения находим

где x - число, заключенное между числами x и  . Поскольку функция
. Поскольку функция  непрерывна в точке х, то при
непрерывна в точке х, то при 
 . Поэтому из последней формулы находим
. Поэтому из последней формулы находим


Замечание 1. Аналогично доказывается теорема о существовании первообразной у непрерывной на сегменте  функции. Отметим, что в этом случае в качестве нижнего предела интегрирования с можно взять а.
функции. Отметим, что в этом случае в качестве нижнего предела интегрирования с можно взять а.
|
|
|
Замечание 2. При доказательстве теоремы мы установили существование производной от интеграла с переменным верхним пределом и доказали, что эта производная равна подынтегральной функции.
 (1)
(1)
2. Основная формула интегрального исчисления.
Любые две первообразные данной функции  отличаются на постоянную. Поэтому, согласно теореме 1 и замечанию 1 к этой теореме, можно утверждать, что любая первообразная
отличаются на постоянную. Поэтому, согласно теореме 1 и замечанию 1 к этой теореме, можно утверждать, что любая первообразная  непрерывной на сегменте
непрерывной на сегменте  функции
функции  имеет вид
имеет вид

где С — некоторая постоянная.
Полагая в последней формуле сначала  , а затем
, а затем 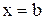 и используя свойство определенных интегралов, найдем
и используя свойство определенных интегралов, найдем

Из этих равенств вытекает соотношение
 (2)
(2)
называемое основной формулой интегрального исчисления или формулой Ньютона - Лейбница.
Итак, для вычисления определенного интеграла от непрерывной функции  нужно составить разность значений произвольной ее первообразной для верхнего и нижнего пределов интегрирования.
нужно составить разность значений произвольной ее первообразной для верхнего и нижнего пределов интегрирования.
Отметим, что основная формула интегрального исчисления открывает широкие возможности для вычисления определенных интегралов, поскольку задача вычисления определенного интеграла сводится к задаче разыскания первообразной функции.
|
|
|
Формулу (2) иногда записывают в иной форме. Именно разность  обозначают символом
обозначают символом 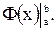 Тогда
Тогда
 (3)
(3)
Рассмотрим несколько примеров:
1) 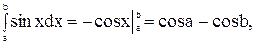
2) 
3) 
4) 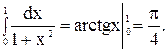
Пусть функция  непрерывна на отрезке
непрерывна на отрезке  симметричном относительно точки
симметричном относительно точки  . Тогда,
. Тогда,

Дата добавления: 2019-09-02; просмотров: 165; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
