Розрахунок енергії зондуючого сигналу
Оскільки перед РЛС, параметри якої потрібно розрахувати, відповідно до вихідних даних не ставиться задача розрізняння цілей за радіальною швидкістю, то в ній можна застосувати узгоджену внутріперіодну обробку і некогерентну міжперіодну обробку 
- імпульсної пачки. Для цього випадку максимальна віддаль дії визначається співвідношенням:
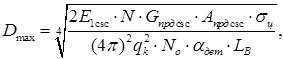(1.26)
де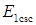 
- імпульсна енергія випроміненого імпульсу, Дж;
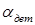- коефіцієнт втрат при некогерентній обробці послідовності із N імпульсів;
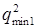- граничне відношення сигнал/шум на виході узгодженого з одним із імпульсів фільтру, який забезпечує потрібну якість виявлення при когерентній обробці.
З урахуваннями (1.26) енергія зондуючого сигналу в одному імпульсі 
визначається співвідношенням:
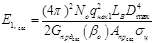. (1.26)
.
Енергія 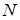- імпульсного пакету, що приймається, буде рівнятись
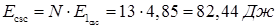. (1.27)
Із розрахованої енергії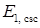 
і заданої потужності 
можна визначити протяжність одного радіоімпульсу зондуючого сигналу
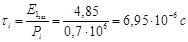. (1.28)
Для перевірки коректності приведених розрахунків необхідно виконати контрольний розрахунок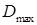 
:
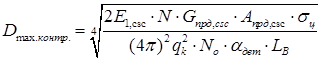, (1.29)
,
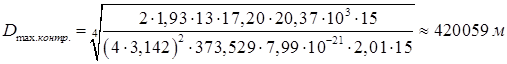і визначити відносну похибку:
. (1.30)
. (1.31)
Перевіряємо виконання умови
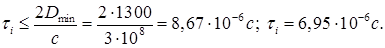(1.32)
Умова виконується.
Вибір і опис зондуючого сигналу
Вибір зондуючого сигналу
Коефіцієнт стиснення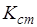 
сигналу (база) визначається як добуток ширини його спектру на тривалість:
|
|
|
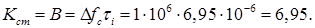(2.1)
Характер та якість інформації, що вилучається РЛС з прийнятого коливання, залежать від структури та властивостей зондуючого сигналу. Призначення РЛС в значній мірі визначає властивості зондуючого сигналу, тому що навіть теоретично не існує радіолокаційного сигналу, який би ідеально підходив би для будь-яких застосувань.
На вибір зондуючого сигналу впливають віддаль виявлення цілей, роздільна здатність РЛС, невизначеності різного виду, точність визначення параметрів радіолокаційного сигналу, практичне виконання пристроїв генерації, випромінювання та обробки сигналу та інші загальні вимоги. Ці фактори часто суперечать один одному (як теоретично, так і практично). Тому при виборі зондуючого сигналу часто доводиться вдаватися до компромісних рішень.
Виходячи із оптимізованих даних, отриманих у п.1 зондуючий сигнал повинен бути складним база якого дорівнює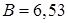 
. При такій базі краще вибрати біфазний сигнал (БФ), оскільки при малій базі сигналу, спектр ЛЧМ-сигналу є нерівномірним, що призводить до важкості реалізації узгодженого фільтру.
Біфазний сигнал на основі кодів Баркера, які при непарних 
існують лише при 
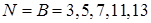, що витікає з виразів: при парному :
|
|
|
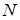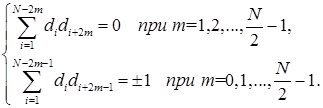(2.2)
при непарному :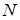
(2.3)
Кореляційна функція кодів Баркера при F = 0: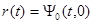 
:
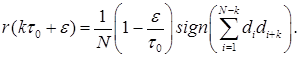(2.4)
Іншим перерізом цієї функції (площиною t = 0) є:
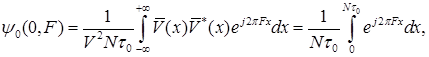(2.5)
яке приводить до рівняння:
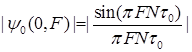. (2.6)
При цьому побічні максимуми менші головного максимуму приблизно в 5 разів. Складні сигнали кодів Баркера також мають наступні переваги перед іншими складними сигналами:
відносно малу тривалість головного викиду;
переважно велике перевищення центрального викиду над боковими;
Отже послідовність коду Баркера для 
наступна:
| N |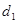 
| 
| 
| 
| 
| 
| 
|
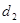
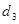
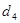
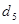
| 7 | +1 | +1 | +1 | -1 | -1 | +1 | -1 |
Дата добавления: 2019-09-02; просмотров: 421; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!