Геометрический смысл дифференциала
Лекция № 1
Основные правила дифференцирования
Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.
1) (u v) = u v
2) (uv) = uv + uv
3) 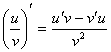 , если v 0
, если v 0
Эти правила могут быть легко доказаны на основе теорем о пределах.
Производные основных элементарных функций:
1)С = 0; 9) 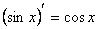
2)(xm) = mxm-1; 10) 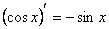
3) 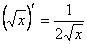 11)
11) 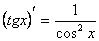
4) 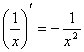 12)
12) 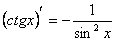
5) 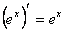 13)
13) 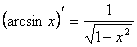
6) 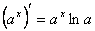 14)
14) 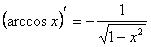
7) 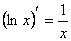 15)
15) 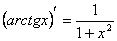
8) 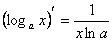 16)
16) 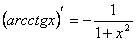
Логарифмическое дифференцирование
Дифференцирование многих функций упрощается, если их предварительно прологарифмировать. Для этого поступают следующим образом. Если требуется найти y' из уравнения y=f(x), то можно:
1. Прологарифмировать обе части уравнения (по основанию е) ln y = ln f(x) = j(x).
2. Продифференцировать обе части равенства, считая ln y сложной функцией от переменной x: 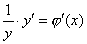 .
.
3. Выразить y' = y·j'(x) = f(x)·(lnx)'.
Примеры.
1. y = xa – степенная функция с произвольным показателем.
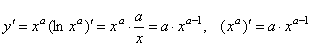 .
.
2. 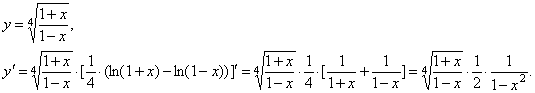
Показательно-степенная функция и ее дифференцирование
Показательно-степенной функцией называется функция вида y = uv, где u=u(x), v=v(x).
Логарифмическое дифференцирование применяется для нахождения производной от показательно-степенной функции.
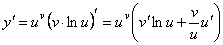
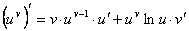
Примеры
1. 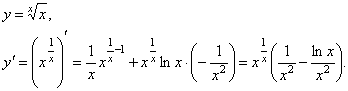
2. 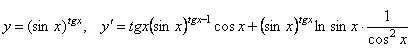 .
.
Таблица производных
Объединим в одну таблицу все основные формулы и правили дифференцирования, выведенные ранее. Всюду будем полагать u=u(x), v=v(x), С=const. Для производных основных элементарных функций будем пользоваться теоремой о производной сложной функции.
|
|
|
1. 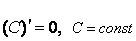 .
.
2. 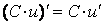 .
.
3. 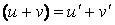 .
.
4. 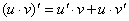 .
.
5. 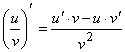 .
.
а) 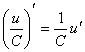 .
.
б) 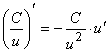 .
.
6. 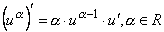 .
.
7. 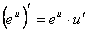 .
.
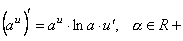 .
.
8. 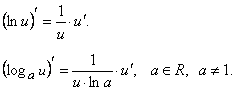
9. 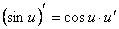 .
.
10. 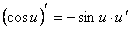 .
.
11. 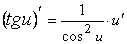 .
.
12. 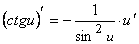 .
.
13. 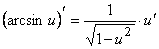 .
.
14. 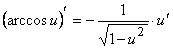 .
.
15. 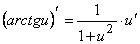 .
.
16. 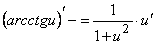 .
.
17. 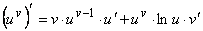 .
.
Примеры
1. 
2. 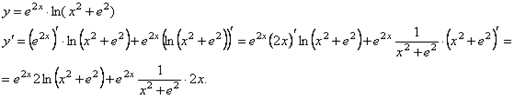
3. 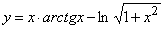 . Найти y'(–1).
. Найти y'(–1).

Производная обратных функций
Пусть требуется найти производную функции у = f(x) при условии, что обратная ей функция x = g(y) имеет производную, отличную от нуля в соответствующей точке.
Для решения этой задачи дифференцируем функцию x = g(y) по х:
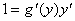
т.к. g(y) 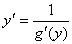
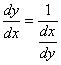
т.е. производная обратной функции обратна по величине производной данной функции.
Пример. Найти формулу для производной функции arctg.
Функция arctg является функцией, обратной функции tg, т.е. ее производная может быть найдена следующим образом:
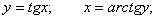
Известно, что 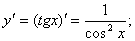
По приведенной выше формуле получаем:
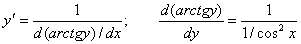
Т.к. 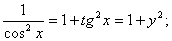 то можно записать окончательную формулу для производной арктангенса:
то можно записать окончательную формулу для производной арктангенса:
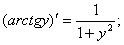
Понятие дифференциала функции. Связь между дифференциалом и производной
Пусть функция y=f(x) дифференцируема на отрезке [a; b]. Производная этой функции в некоторой точке х0 [a; b] определяется равенством
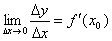
Следовательно, по свойству предела
|
|
|
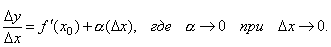
Умножая все члены полученного равенства на Δx, получим:
Δy = f '(x0)·Δx + a·Δx.
Итак, бесконечно малое приращение Δy дифференцируемой функции y=f(x) может быть представлено в виде суммы двух слагаемых, из которых первое есть (при f '(х0) ≠ 0) главная часть приращения, линейная относительно Δx, а второе – бесконечно малая величина более высокого порядка, чем Δx. Главную часть приращения функции, т.е. f '(х0)·Δx называют дифференциалом функции в точке х0 и обозначают через dy.
Таким образом, если функция y=f(x) имеет производную f '(x) в точке x, то произведение производной f '(x) на приращение Δx аргумента называют дифференциалом функции и обозначают:
| dy = f '(x)·Δx | (1) |
Найдем дифференциал функции y= x. В этом случае y' = (x)' = 1 и, следовательно, dy=dx=Δx. Таким образом, дифференциал dxнезависимой переменной xсовпадает с ее приращением Δx. Поэтому формулу (1) мы можем записать так:
| dy = f '(x)dx |
Но из этого соотношения следует, что 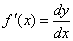 . Следовательно, производную f '(x) можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.
. Следовательно, производную f '(x) можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.
Ранее мы показали, что из дифференцируемости функции в точке следует существование дифференциала в этой точке.
|
|
|
Справедливо и обратное утверждение.
Если для данного значения x приращение функции Δy = f(x+Δx) – f(x) можно представить в виде Δy = A·Δx + α, где α – бесконечно малая величина, удовлетворяющая условию 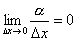 , т.е. если для функции y=f(x) существует дифференциал dy=A·dx в некоторой точке x, то эта функция имеет производную в точке x и f '(x)=А.
, т.е. если для функции y=f(x) существует дифференциал dy=A·dx в некоторой точке x, то эта функция имеет производную в точке x и f '(x)=А.
Действительно, имеем 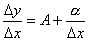 , и так как
, и так как 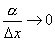 при Δx→0, то
при Δx→0, то 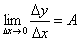 .
.
Таким образом, между дифференцируемостью функции и существованием дифференциала имеется очень тесная связь, оба понятия равносильны.
Примеры. Найти дифференциалы функций:
1. 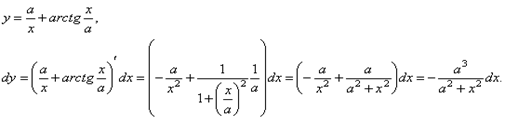
2. 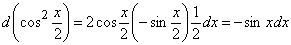 .
.
Геометрический смысл дифференциала
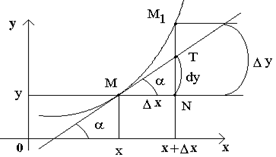
Рассмотрим функцию y=f(x) и соответствующую ей кривую. Возьмем на кривой произвольную точку M(x; y), проведем касательную к кривой в этой точке и обозначим через α угол, который касательная образует с положительным направлением оси Ox. Дадим независимой переменной x приращение Δx, тогда функция получит приращение Δy = NM1. Значениям x+Δx и y+Δy на кривой y = f(x) будет соответствовать точка
M1(x+Δx; y+Δy).
Из ΔMNT находим NT=MN·tg α. Т.к. tg α = f '(x), а MN = Δx, то NT = f '(x)·Δx. Но по определению дифференциала dy=f '(x)·Δx, поэтому dy = NT.
|
|
|
Таким образом, дифференциал функции f(x), соответствующей данным значениям x и Δx, равен приращению ординаты касательной к кривой y=f(x) в данной точке х.
Дата добавления: 2019-07-15; просмотров: 199; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
