Теорема об инвариантности дифференциала
Ранее мы видели, что если u является независимой переменной, то дифференциал функции y=f '(u) имеет вид dy = f '(u)du.
Покажем, что эта форма сохраняется и в том случае, когда u является не независимой переменной, а функцией, т.е. найдем выражение для дифференциала сложной функции. Пусть y=f(u), u=g(x) или y = f(g(x)). Тогда по правилу дифференцирования сложной функции:
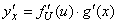 .
.
Следовательно, по определению
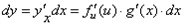 ,
,
но g'(x)dx= du, поэтому dy= f'(u)du.
Мы доказали следующую теорему.
Теорема. Дифференциал сложной функции y=f(u), для которой u=g(x), имеет тот же вид dy=f'(u)du, какой он имел бы, если бы промежуточный аргумент u был независимой переменной.
Иначе говоря, форма дифференциала не зависит от того, является аргумент функции независимой переменной или функцией другого аргумента. Это свойство дифференциала называется инвариантностью формы дифференциала.
Пример. 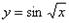 . Найти dy.
. Найти dy.
Учитывая свойство инвариантности дифференциала, находим
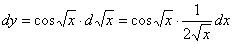 .
.
Применение дифференциала к приближенным вычислениям
Пусть нам известно значение функции y0=f(x0) и ее производной y0' = f '(x0) в точке x0. Покажем, как найти значение функции в некоторой близкой точке x.
Как мы уже выяснили приращение функции Δyможно представить в виде суммы Δy=dy+α·Δx, т.е. приращение функции отличается от дифференциала на величину бесконечно малую. Поэтому, пренебрегая при малых Δx вторым слагаемым в приближенных вычислениях, иногда пользуются приближенным равенством Δy≈dyили Δy»f'(x0)·Δx.
|
|
|
Т.к., по определению, Δy = f(x) – f(x0), то f(x) – f(x0)≈f'(x0)·Δx.
Откуда
| f(x) ≈ f(x0) + f'(x0)·Δx |
Примеры:
1. y = x2 – 2x. Найти приближенно, с помощью дифференциала, изменение y (т.е. Δy), когда x изменяется от 3 до 3,01.
Имеем Δy≈dy=f'(x)·Δx.
f'(x)=2x – 2 ,f'(3)=4, Δx=0,01.
Поэтому Δy ≈ 4·0,01 = 0,04.
2. Вычислить приближенно значение функции 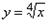 в точке x = 17.
в точке x = 17.
Пусть x0= 16.
Тогда Δx = x – x0= 17 – 16 = 1,
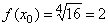 ,
,
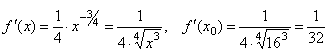 .
.
Таким образом, 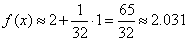 .
.
3. Вычислить ln 0,99.
Будем рассматривать это значение как частное значение функции y=lnx при х=0,99.
Положим x0 = 1. Тогда Δx = – 0,01, f(x0)=0.
 , f '(1)=1.Поэтому f(0,99) ≈ 0 – 0,01 = – 0,01.
, f '(1)=1.Поэтому f(0,99) ≈ 0 – 0,01 = – 0,01.
Дата добавления: 2019-07-15; просмотров: 620; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
