Симметричные двойственные задачи
Рассмотрим задачу производственного планирования. Пусть предприятие имеет m видов ресурсов объемом 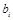 единиц. Эти ресурсы должны быть использованы для выпуска n видов продукции. Пусть
единиц. Эти ресурсы должны быть использованы для выпуска n видов продукции. Пусть 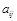 – норма потребления i-го вида ресурса на производство единицы j-ой продукции;
– норма потребления i-го вида ресурса на производство единицы j-ой продукции; 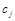 – цена реализации j-ой продукции;
– цена реализации j-ой продукции; 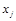 – объем производства j-ой продукции, обеспечивающий предприятию максимальную выручку.
– объем производства j-ой продукции, обеспечивающий предприятию максимальную выручку.
План производства 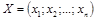 следует составить из условия максимизации общей стоимости продукции
следует составить из условия максимизации общей стоимости продукции 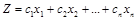 при ограничениях на использовании ресурсов
при ограничениях на использовании ресурсов
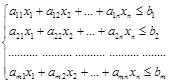
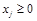 ,
, 
Или в краткой форме записи математическая модель задачи имеет вид:
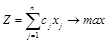 (1)
(1)
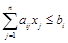 ,
, 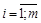 (2)
(2)
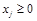 ,
,  (3)
(3)
Задачу (1) – (3) называют исходной.
По исходным данным задачи (1) – (3) сформируем другую экономическую задачу.
Предположим, что предприятию разрешено на его усмотрение реализовать все указанные ресурсы. Необходимо установить цены на них – 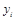 ,
, 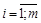 , пользуясь следующими соображениями:
, пользуясь следующими соображениями:
– покупатель стремится минимизировать их общую стоимость;
– предприятие согласно продать по ценам, дающим прибыль не меньшую, чем выручка, которую оно может получить от реализации изготовленной продукции.
Эти требования можно записать в виде следующей ЗЛП:

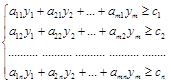
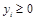 ,
, 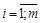
Или в краткой форме записи:
|
|
|
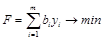 (4)
(4)
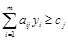 ,
,  (5)
(5)
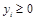 ,
, 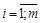 (6)
(6)
Полученную задачу (4) – (6) называют двойственной. Переменные 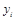 называются двойственными оценками, или теневыми ценами.
называются двойственными оценками, или теневыми ценами.
Задачи (1) – (3) и (4) – (6) называют парой взаимно двойственных симметричных задач, т. к. они обладают следующими свойствами:
1. Если в одной задаче ищется максимум целевой функции, то в другой – минимум.
2. Коэффициенты при переменных в целевой функции одной задачи являются правыми частями ограничений другой задачи и, наоборот.
3. В каждой задаче система ограничений задается в виде неравенств, причем все они одного смысла: если задача на max, то все неравенства содержат знаки « 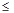 », если на min, то все неравенства содержат знаки «
», если на min, то все неравенства содержат знаки « 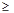 ».
».
4. Матрицы ограничений прямой и двойственной задач являются транспонированными друг к другу.
5. Число неравенств в системе ограничений одной задачи равно числу переменных другой задачи.
6. Условие неотрицательности переменных сохраняется в обеих задачах.
Примечание: Понятие «прямой» и «двойственной» задач условно.
Построение модели двойственной задачи
|
|
|
Используя свойства (1–6), покажем на конкретном примере построение двойственной задачи.
Пример. Пусть исходная задача имеет вид:

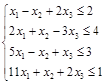
 ,
, 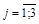
Нужно составить к ней двойственную.
Решение. Запишем расширенную матрицу системы ограничений и транспонируем ее.
| 1 | –1 | 2 | 2 | 1 | 2 | 5 | 11 | 2 | |||
| 2 | 1 | –3 | 4 | АТ= | –1 | 1 | –1 | 1 | 3 | ||
| А = | 5 | –1 | 1 | 3 | 2 | –3 | 1 | 2 | 1 | ||
| 11 | 1 | 2 | 1 | 2 | 4 | 3 | 1 | min | |||
| 2 | 3 | 1 | max |
Теперь запишем двойственную задачу по АТ с переменными 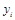 ,
, 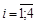 .
.
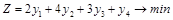
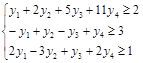
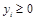 ,
, 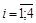 .
.
Пример. К заданной задаче записать двойственную:
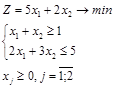
Решение. Так как задача на min, то все неравенства должны иметь знаки « 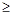 ». С этой целью второе ограничение умножим на (–1); при этом знак неравенства изменится на противоположный. Теперь задача будет иметь вид:
». С этой целью второе ограничение умножим на (–1); при этом знак неравенства изменится на противоположный. Теперь задача будет иметь вид:
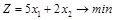

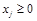 ,
, 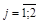
Запишем матрицы А и АТ.
| 1 | 1 | 1 | 1 | –2 | 5 | |||
| А = | –2 | –3 | –5 | АТ= | 1 | –3 | 2 | |
| 5 | 2 | min | 1 | –5 | max |
Двойственная задача:

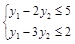
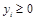 ,
, 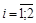 .
.
Дата добавления: 2019-07-15; просмотров: 197; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
