Розподіл імовірностей випадкових похибок
Результати вимірів е випадковими оскільки передбачити їх величину неможливо. Тоді і їх похибки будуть випадковими і для них можна вказати лише межу, в яких вони змінюються згідно з першою властивістю.
Неперервні випадкові похибки можна характеризувати законом розподілу, як об'єктивно існуючим зв'язком між випадковими величинами і їх імовірностями.
При багаторазових випробуваннях закон розподілу ряду істинних випадкових похибок можна характеризувати функціями:
1. Інтегральною функцією розподілу
( 
)
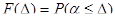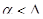2. Функцією щільності
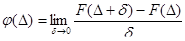
де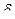 
- приріст випадкової похибки 
.
Звернемося до постулату Гаусса, згідно з яким найбільш імовірним значенням шуканої величини є середнє арифметичне Із результатів повторних вимірювань. Скористаємося теоремою:
Якщо випадкові похибки відповідають постулату Гаусса, то законом розподілу випадкових похибок буде нормальний закон. В методі максимальної правдоподібності Фішера також доведено, що для нормального закону розподілу випадкових величин оцінкою параметра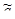 
є середнє арифметичне.
Функція щільності нормального розподілу випадкових похибок визначиться за формулою
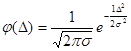
Для нормованих похибок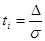 
отримаємо
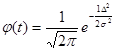
Числові характеристики рівноточних вимірів
Рівноточними, називають виміри, дисперсії яких рівні між собою, тобто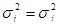 
. Тому рівноточні виміри можна виразити статистичним рядом
|
|
|
( )
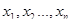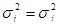Якщо невідоме істинне значення вимірюваної величини Х, то необхідно знайти значення близьке до істинного. Його називають дійсним, або ймовірним значенням виміряної величини. Воно може бути прийнятим, коли точність вимірів задовольняє поставленим вимогам, або - відхилене. Тому постає задача обчислення за результатами вимірів показників як розміру шуканої величини, так і її точності, їх називають числовими характеристиками. В теорії похибок вимірів до числових характеристик відносять:
1. Середнє арифметичне
Використаємо ряд вимірів. Якщо відоме істинне значення вимірюваної величини X, то визначимо ряд істинних похибок
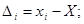
Складемо їх і поділимо на n
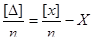
За четвертою властивістю компенсації випадкових похибок 
ліва
частина формули наближається до нуля при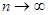 
. Позначимо середнє арифметичне
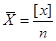
Тоді отримаємо ймовірне співвідношення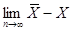 
Принцип арифметичного середнього показує, що при нескінченній кількості вимірів і відсутності систематичних похибок просте арифметичне середнє наближається до істинного значення.
Це означає, що середнє арифметичне X буде найбільш точним, або ймовірніш значенням виміряної величини.
|
|
|
Як виміри, так і похибки вимірів при дотриманні "комплексу умов" належать нормальному закону розподілу. Тоді і за методом ММП Фішера доведено, що середнє арифметичне буде найбільш близьким до істинного.
Практично число вимірів обмежене, тому і обчислене середнє арифметичне буде випадковою величиною, яка може приймати значення в деякому інтервалі, який залежить від числа вимірів та прийнятої довірчої ймовірності.
2. Середня квадратична похибка окремого виміру
Теоретично мірою точності вимірів є дисперсія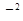 
. За результатами статистичної обробки рядів вимірів визначають емпіричну (або статистичну) дисперсію m2
За ММП Фішера доведено, що коли статистичний ряд, підкоряється нормальному закону розподілу, ефективною точності є дисперсія
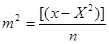
Оскільки розмірність дисперсії ("в квадраті"), то за міру точності приймають емпіричний стандарт або середню квадратичну похибку
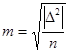
де 
- істинні похибки.
Її називають похибкою Гаусса.
Якщо невідоме істинне значення вимірювальної величини, то використовуємо різниці
,
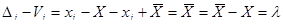де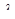 
- систематична похибка.
Коли число вимірів дорівнює n, із формули отримаємо:
, 
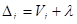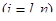
Зведемо вираз до квадрату і підсумуємо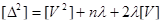 
|
|
|
Якщо в формулі взяти суму ймовірних похибок V, отримаємо:
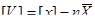
Оскільки середнє арифметичне за формулою дорівнює 
, то в формулі отримаємо:
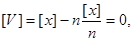
або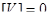 
Формула використовується і для контролю обчислення ймовірних похибок V.
Тоді формула зведеться до вигляду
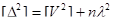
Істинна похибка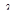 
простої арифметичної середини обчислюється за формулою:
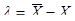або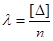 
.
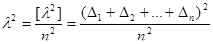
Згідно з четвертою властивістю випадкових похибок
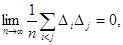
з врахуванням попередніх формул отримаємо
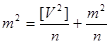
Остаточно отримаємо формулу Бесселя для визначення середньої квадратичної похибки виміру за ймовірними похибками
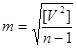
3. Середня квадратична похибка арифметичної середини
Запишемо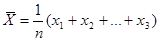 
Оскільки виміри рівноточні, тобто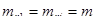 
, а часткові похідні 
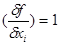, то за формулою отримаємо дисперсію середнього арифметичного
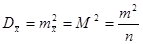
Тоді середня квадратична похибка арифметичного середнього арифметичного буде
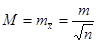
Додатково обчислюють:
4. Середню квадратичну похибку середньої квадратичної похибки
5. Середню квадратичну похибку середньої квадратичної похибки арифметичного середнього
Для оцінки точності похибок вимірів використовують інші критерії.
|
|
|
6. Середню похибку 
, як середнє арифмитичне із суми абсолютних випадкових значень похибок, тобото
7. Середню похибку r. Її визначають в середині зростаючого ряду складеного із абсолютних значень похибок вимірів. Тоді ймовірність серединної похибки буде
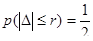
Середня квадратична похибка виміру m має зв’язок середньою та серединною r похибками
;
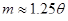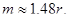
8. Абсолютні похибки. До них належать: середня квадратична (m), середня квадратична арифметичного середнього (М), середня ( ), серединна (r), істинна (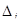 
), ймовірна (Vi) і гранична ( 
)
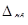9. Відносні похибки. Відношення абсолютної похибки до значення виміряної величини називають відносною похибкою.
Назва відносної похибки відповідає назві абсолютної похибки, наприклад:
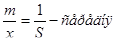квадратична відносна похибка;
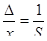- істинна відносна похибка.
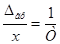- гранична відносна похибка тощо.
Оцінка точності вимірів за допомогою середніх квадратичних похибок m порівняно з середньою та серединною похибками має переваги:
1. Обгрунтованості: ймовірність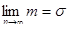 
, тобто при умовах коли число вимірів прямує до нескінченності, середня квадратична похибка прямує до абсолютного значення стандарту.
2. Ефективності: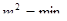 
, тобто значення дисперсії буде мінімальним.
3. На величину середньої квадратичної похибки m вплив більших за абсолютним значенням похибок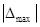 
найбільший.
4. Середня квадратична похибка m зв’язана з граничною похибкою відношенням
,
де t – вибирається із таблиць розподілу Лапласа або Стюдента залежить від надійної ймовірності p та кількості вимірів n.
5. Середня квадратична похибка визначається достатньо надійно при обмеженій кількості вимірів.
Дата добавления: 2019-07-15; просмотров: 177; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!