Цей результат за допомогою теореми Штольца виходить відразу
2. Застосуємо теорему Штольца до доказу наступної цікавої пропозиції (Коші):
Якщо варіанта ап має межа (кінцева або нескінченний), то та ж межа має й варіанта
(«середнє арифметичне» перших п значень варіанти ап).
Дійсно, думаючи по теоремі Штольца
маємо:
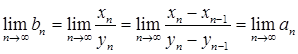
Наприклад, якщо ми знаємо, що 
, те й
3. Розглянемо тепер варіанту (уважаючи до - натурального)
,
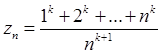яка представляє невизначеність виду 
.
Думаючи в теоремі Штольца
будемо мати
АЛЕ 
так що 
використовуючи наступне твердження
,
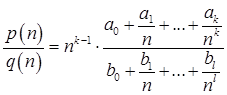
Другий множник тут має кінцева межа 
. Якщо ступеня багаточленів рівні k = l, то межа відносини багаточленів дорівнює межі відносини коефіцієнтів при старших ступенях багаточленів.
Якщо k < l, то розглянуте відношення прагне до 
Якщо k > l, то розглянуте відношення прагне до 
у підсумку ми одержуємо
Висновок
У даній роботі ми розглянули теорему Штольца і її застосування на практиці. Розглянуті приклади показують, що дана теорема в достатній мері полегшує процес знаходження меж невизначених виражень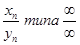 
, допомагаючи обчислити шукану межу, не прибігаючи до допоміжних нерівностей.
Список літератури
1. Г.М. Фихтенгольц. Курс диференціального й інтегрального вирахування. – К., 2004
2. Б.П. Демидович. Збірник задач і вправ по математичному аналізі. - К., 2001
3. Л.Д. Кудрявцев. Курс математичного аналізу, т. 1. - К., 1998.
Дата добавления: 2019-07-15; просмотров: 154; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!