Геометрична інтерпретація стандартної задачі
Геометрична інтерпретація аналітичних задач дає можливість наочно представити їх структуру, що сприяє засвоєнню їхніх основних властивостей та відкриває шляхи виявлення і дослідження інших, більш складних властивостей цих задач. У найпростіших випадках геометричне подання дає змогу знайти розв'язок задачі, однак навіть у тривимірному просторі геометричне розв'язування ускладнюється і створює ряд труднощів у побудові відповідних геометричних фігур, а в просторах вимірності, більшої за три, таке розв'язування і зовсім неможливе.
Можливі різноманітні форми і способи геометричного представлення задач лінійного програмування. Доцільність вибору кожного способу зумовлюється метою, якої хочуть досягти даною геометричною інтерпретацією та особливостями структури самої задачі, в тому числі й формою її представлення.
Для геометричної інтерпретації візьмемо основну задачу лінійного програмування у другій стандартній формі. Для наочності розглянемо найпростіший випадок, коли в системі обмежень (26) і цільовій функції (25) є лише дві змінних 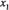 ,
, 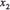
Розглянемо розв'язування нерівностей.
Лема 3. Множина розв'язків нерівності з двома змінними
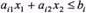
є однією з двох півплощин, на які вся площина ділиться прямою  , включаючи й цю пряму, а інша півплощина з тією ж прямою є множиною розв'язків нерівності
, включаючи й цю пряму, а інша півплощина з тією ж прямою є множиною розв'язків нерівності
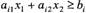
Доведення. Гранична пряма 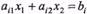 перпендикулярна до вектора нормалі .
перпендикулярна до вектора нормалі . 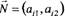 (рис 3.1). Вектор нормалі (його ще називають напрямним вектором ) є градієнтом лінійної функції
(рис 3.1). Вектор нормалі (його ще називають напрямним вектором ) є градієнтом лінійної функції  і показує напрям зростання її значень
і показує напрям зростання її значень 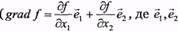 — одиничні вектори вздовж осей
— одиничні вектори вздовж осей 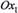 і
і  відповідно; таким чином,
відповідно; таким чином, 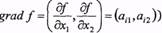 . Справді, нехай
. Справді, нехай 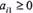 ,
,  . Візьмемо на прямій, яка визначається вектором
. Візьмемо на прямій, яка визначається вектором 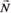 точку
точку  , причому нехай
, причому нехай 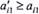 , тобто точка
, тобто точка  лежить далі від початку координат, ніж точка
лежить далі від початку координат, ніж точка 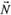 . Очевидно також, що
. Очевидно також, що  . У точці
. У точці 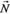 числове значення
числове значення 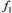 лінійної функції
лінійної функції 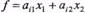 дорівнює
дорівнює 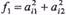 . Аналогічно в точці
. Аналогічно в точці 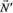 значення
значення 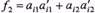 . Ураховуючи, що
. Ураховуючи, що 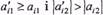 , дістанемо
, дістанемо 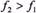
|
|
|
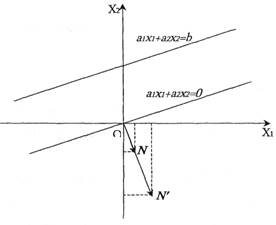
Рис. 1.
Аналогічно можна пересвідчитись, що напрям зменшення значень лінійної функції  збігається з напрямним вектором
збігається з напрямним вектором 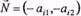
Прямі лінії на площині 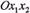 , які паралельні прямій, що визначається рівнянням
, які паралельні прямій, що визначається рівнянням 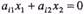 називають лініями рівнів лінійної функції
називають лініями рівнів лінійної функції 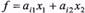 . Користуючись поняттям напрямного вектора
. Користуючись поняттям напрямного вектора 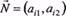 , можемо визначити розміщення півплощин
, можемо визначити розміщення півплощин  і
і 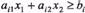 на координатній площині
на координатній площині 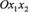 . Півплощина
. Півплощина 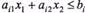 розміщена по той бік прямої
розміщена по той бік прямої  , куди показує напрямний вектор -
, куди показує напрямний вектор - 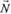 . Аналогічно вектор
. Аналогічно вектор 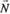 показує, де розміщена півплощина
показує, де розміщена півплощина 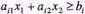 відносно прямої
відносно прямої 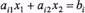 побудуємо напрямний вектор N = (3,-2). Напрямний вектор міститься у шуканій півплощині, яка виділена штриховими лініями (рис 3.2).
побудуємо напрямний вектор N = (3,-2). Напрямний вектор міститься у шуканій півплощині, яка виділена штриховими лініями (рис 3.2).
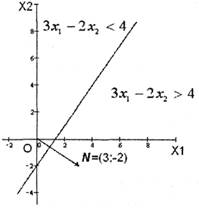
Рис. 3.2
Якщо врахувати, що множина точок, що задовольняє рівняння
|
|
|
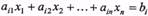 29.)
29.)
при п = 3, є півплощина, а при п > 3 - гіперплощина в n-вимірному просторі, то лему 3 можна поширити на випадок трьох і більше змінних.
Теорема 2. Множиною всіх розв'язків лінійної нерівності з п змінними
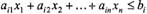
є одним з півпросторів, на які весь простір розділяється площиною або гіперплощиною (29), включаючи й саму площину (гіперплощину).
Розглянемо множину розв'язків систем нерівностей.
Теорема 3. Множиною розв'язків сумісної системи т лінійних нерівностей з двома змінними
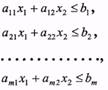
є опуклим многокутником.
Доведення. Кожна з нерівностей у відповідності з лемою 3 визначає одну з півплощин, які є опуклими множинами точок. Множиною розв'язків сумісної системи лінійних нерівностей є множина точок, які належать півплощинам-розв'язкам усіх нерівностей, тобто належать їх перетину. Згідно теореми 2 про перетин опуклих множин ця множина є опуклою і містить скінчене число кутових точок, тобто є опуклим многокутником.
Теорема 4. Множина розв'язків сумісної системи т лінійних нерівностей з п змінними є опуклим многогранником в n-вимірному просторі.
|
|
|
Теорема 5. Множиною всіх допустимих розв'язків сумісної системи т лінійних рівнянь з п змінними ( 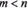 ) є опуклим многогранником в n-вимірному просторі.
) є опуклим многогранником в n-вимірному просторі.
Теорема 6. Оптимальне значення задачі лінійного програмування досягається у вершині многогранника розв'язків системи обмежень.
Результати цього підрозділу дають змогу так інтерпретувати задачі лінійного програмування:
У многограннику (многокутнику у випадку двох змінних) розв'язків системи обмежень задачі лінійного програмування знайти таку вершину, де цільова функція набуває оптимального (найбільшого або найменшого) значення.
Нехай фермер прийняв рішення вирощувати озиму пшеницю і цукрові буряки на площі 20 га, відвівши під цукрові буряки не менше як 5 га. Техніко-економічні показники вирощування цих культур маємо у табл. 2:
Таблиця 2 Показники вирощування сільськогосподарських культур
| Показник (із розрахунку на 1 га) | Озима пшениця | Цукрові буряки | Наявний ресурс |
| Затрати праці, людино-днів | 5 | 25 | 270 |
| Затрати праці механізаторів, людино-днів | 2 | 8 | 80 |
| Урожайність, тонн | 3,5 | 40 | — |
| Прибуток, тис. грн. | 0,7 | 1 | — |
Критерієм оптимальності є максимізація прибутку.
Запишемо економіко-математичну модель структури виробництва озимої пшениці та цукрових буряків, ввівши такі позначення:
|
|
|
x1 — шукана площа посіву озимої пшениці, га;
x2— шукана площа посіву цукрових буряків, га.
Задача лінійного програмування має такий вигляд:
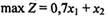 (38)
(38)
за умов:
 (39)
(39)
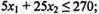 (40)
(40)
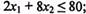 (41)
(41)
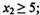 (42)
(42)
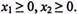 (43)
(43)
Геометричну інтерпретацію задачі зображено на рис. 2.2.
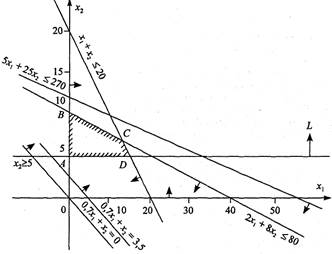
Рис. 2.2. Область допустимих розв'язків задачі
Область допустимих розв'язків цієї задачі дістаємо так. Кожне обмеження, наприклад 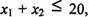 задає півплощину з граничною прямою
задає півплощину з граничною прямою 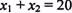 . Будуємо її і визначаємо півплощину, яка описується нерівністю
. Будуємо її і визначаємо півплощину, яка описується нерівністю  .З цією метою в нерівність
.З цією метою в нерівність 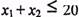 підставляємо координати характерної точки, скажімо,
підставляємо координати характерної точки, скажімо, 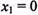 і
і  . Переконуємося, що ця точка належить півплощині
. Переконуємося, що ця точка належить півплощині 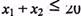 . Цей факт на рис. 2.2 ілюструємо відповідною напрямленою стрілкою. Аналогічно будуємо півплощини, які відповідають нерівностям (39)—(43). У результаті перетину цих півплощин утворюється область допустимих розв'язків задачі (на рис. 2.2 — чотирикутник ABCD). Цільова функція Z = 0,7x1+х2 являє собою сім'ю паралельних прямих, кожна з яких відповідає певному значенню Z. Зокрема, якщо Z=0, то маємо Z = 0,7x1+х2=0. Ця пряма проходить через початок системи координат. Коли Z= 3,5, то маємо пряму 0,7x1+х2=3,5.
. Цей факт на рис. 2.2 ілюструємо відповідною напрямленою стрілкою. Аналогічно будуємо півплощини, які відповідають нерівностям (39)—(43). У результаті перетину цих півплощин утворюється область допустимих розв'язків задачі (на рис. 2.2 — чотирикутник ABCD). Цільова функція Z = 0,7x1+х2 являє собою сім'ю паралельних прямих, кожна з яких відповідає певному значенню Z. Зокрема, якщо Z=0, то маємо Z = 0,7x1+х2=0. Ця пряма проходить через початок системи координат. Коли Z= 3,5, то маємо пряму 0,7x1+х2=3,5.
Дата добавления: 2019-07-15; просмотров: 450; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
