Дві стандартні форми задач лінійного програмування
Загальна форма задачі лінійного програмування (3.1) - (3.6) не придатна для побудови досить простих і ефективних методів розв'язування її, причиною чого е неоднорідність системи умов (3.2) -(3.6). Тому, як правило, задачу зводять до стандартної форми.
В залежності від методів, які застосовуються, розрізняють дві стандартні форми:
основна задача лінійного програмування з обмеженнями-рівностями або перша стандартна форма;
основна задача лінійного програмування з обмеженнями-нерівностями або друга стандартна форма.
Формулювання основної задачі лінійного програмування у першій стандартній формі полягає в наступному: серед усіх невід'ємних розв'язків системи основних обмежень-рівнянь знайти такий, при якому цільова функція набуває найбільшого або найменшого значення:
 (21)
(21)
 (22)
(22)
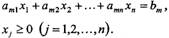 (23)
(23)
Або у короткому запису
 (21а)
(21а)
 (22а)
(22а)
Основна задача лінійного програмування може бути також записана у скалярно-векторній, матричній і векторній формах, якщо скористатись позначеннями:
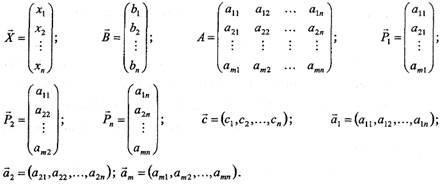
Тут  — вектор-стовпець змінних,
— вектор-стовпець змінних,  — вектор-стовпець вільних членів, А — матриця системи основних обмежень,
— вектор-стовпець вільних членів, А — матриця системи основних обмежень,  - вектор-стовпець матриці А;
- вектор-стовпець матриці А;  — вектор-рядок коефіцієнтів цільової функції,
— вектор-рядок коефіцієнтів цільової функції,  - вектор-рядок матриці А.
- вектор-рядок матриці А.
|
|
|
Скалярно-векторна форма:
 (216)
(216)
 (22б)
(22б)
 (23б)
(23б)
Матрична форма:
 (21в)
(21в)
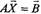 (22в)
(22в)
 (23в)
(23в)
Векторна форма:
 (21г)
(21г)
 (22г)
(22г)
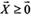 (23г)
(23г)
Лема 1. Будь-яку задачу лінійного програмування у загальній формі можна звести до першої стандартної форми.
|
|
|
Доведення. Покажемо, що будь-яку нерівність, введенням додаткової невідомої можна звести до рівності. Дійсно, нехай деяке обмеження має вигляд

Перепишемо його таким чином:

Введемо позначення 
За побудовою  є невід'ємною величиною. Крім того останнє
є невід'ємною величиною. Крім того останнє
співвідношення є рівняння відносно невідомих 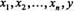 :
:

Отже ми прийшли до рівності еквівалентній вихідної нерівності.
За таким самим алгоритмом можна звести до рівності й нерівність з протилежним знаком, але завжди треба нові невідомі додавати до менших частин нерівностей, бо у протилежному випадку вони не будуть невід'ємними величинами.
Наступний крок полягає в зведені до однорідної системи обмежень на знак. Умови недодатності (3.6) легко перетворюються в умови невід'ємності за допомогою заміни відповідних змінних 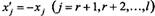 .
.
Складніше позбутися змінних, на знак яких обмежень не накладено. Цього можна досягти двома способами.
1-й спосіб. Якщо число таких змінних (3.7) менше, ніж число обмежень основної групи і вектори-стовпці коефіцієнтів при них разом з деякими іншими утворюють базисний мінор, то, розв'язавши добуту нами систему обмежень-рівностей відносно згаданих змінних, виключаємо їх як з системи умов, так і з цільової функції, залишаючи без уваги формули, що виражають їх через невід'ємні змінні, підставляючи які у залишені вирази, дістаємо й оптимальні значення змінних (3.7).
|
|
|
Хоч цей спосіб придатний для більшості практичних випадків, однак буває, що умови необхідні для його використання, не виконуються.
Тоді цим способом можна виключити лише частину вільних змінних, а до тих, що залишилися у задачі, застосувати 2-й спосіб.
2-й спосіб. Кожну змінну, на знак якої не накладено обмежень, подають у вигляді різниці двох невід'ємних змінних
 (24)
(24)
Визначивши оптимальні значення  та
та  , можемо знайти за (24) і оптимальне значення відповідних
, можемо знайти за (24) і оптимальне значення відповідних 
Приклад 1. Звести до першої стандартної форми таку задачу лінійного програмування:

Розв'язання. Введенням однієї додаткової змінної  та заміною
та заміною  зводимо задачу до вигляду
зводимо задачу до вигляду

Хоч тут кількість змінних без обмеження на знак і менша від кількості основних обмежень, їх не можна вивести з задачі, оскільки вектори-стовпці їхніх коефіцієнтів пропорційні і не можуть разом входити до базисного мінору. Тому виведемо одну з них, а другу замінимо різницею двох невід'ємних змінних.
|
|
|
Запишемо задачу в таблицю (в нульовий рядок записане рівняння, що відповідає цільової функції: 
| № рядка | 
| 
| 
| 
| 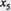
| 
|
| 0 | -6 | 3 | 4 | -5 | 0 | 0 |
| 1 | 2 | -6 | -2 | 
| 0 | 12 |
| 2 | 3 | 1 | -2 | 1 | 0 | 6 |
| 3 | 1 | -1 | -4 | 2 | 1 | 8 |
Вибравши  = 1 ключовим елементом, переходимо до нової таблиці.
= 1 ключовим елементом, переходимо до нової таблиці.
| № рядка | 
| 
| 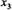
| 
| 
| 
|
| 0 | 4 | -27 | -6 | 0 | 0 | 60 |
| 1 | 2 | -6 | _2 | 1 | 0 | 12 |
| 2 | 1 | 7 | 0 | 0 | 0 | -6 |
| 3 | -3 | 11 | 0 | 0 | 1 | -16 |
Виписуючи окремо 1-й рядок (виразивши з нього,  )
)  і замінивши
і замінивши  , дістаємо першу стандартну форму задачі
, дістаємо першу стандартну форму задачі

де 
Основна задача лінійного програмування у другій стандартній формі полягає в тому, що серед всіх невід'ємних розв'язків системи основних обмежень-нерівностей треба знайти такий, при якому цільова функція буде мати оптимальне значення:
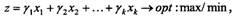 (25)
(25)
 (26)
(26)

 (27)
(27)
Або у короткому запису
 (25а)
(25а)
 (26а)
(26а)
Скалярно-векторна форма:
 (25б)
(25б)
 (26б)
(26б)
 (27б)
(27б)
Матрична форма:
 (25в)
(25в)
 (26в)
(26в)
 (27в)
(27в)
Векторна форма:
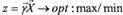 (25г)
(25г)
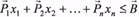 (26г)
(26г)
 (27г)
(27г)
Лема 2. Перша стандартна форма основної задачі лінійного програмування завжди може бути зведена до другої стандартної форми.
Доведення. Припустимо, що невідомі  є вільними;
є вільними;
 - базисними; ранг матриці системи обмежень (22) дорівнює
- базисними; ранг матриці системи обмежень (22) дорівнює 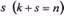
Розв'яжемо систему рівнянь (22) відносно базисних невідомих і нехай розв'язок має вигляд
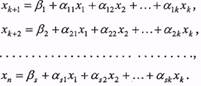 (28)
(28)
Всі невідомі невід'ємні, тому

Враховуючи це, поставимо у відповідність отриманому розв'язку (28) еквівалентну систему нерівностей:

Введемо позначення  і помноживши всі нерівності на -1 отримуємо систему обмежень:
і помноживши всі нерівності на -1 отримуємо систему обмежень:

Очевидно, що остання система обмежень збігається з (26) і рівносильна системі обмежень (3-9) У тому розумінні, що будь-якому розв'язку  системи нерівностей відповідає певний розв'язок
системи нерівностей відповідає певний розв'язок  системи рівнянь (22) Для завершення доведення леми підставимо у цільову функцію (21) замість базисних невідомих
системи рівнянь (22) Для завершення доведення леми підставимо у цільову функцію (21) замість базисних невідомих  їхні вирази (28). Якщо згрупувати подібні члени, то цільова функція набуде вигляду (25). Приклад 2. Звести до другої стандартної форми задачу
їхні вирази (28). Якщо згрупувати подібні члени, то цільова функція набуде вигляду (25). Приклад 2. Звести до другої стандартної форми задачу


Розв'язання. Виписуємо матрицю системи обмежень

і шукаємо ранг матриці. Базисним буде мінор

Отже, ранг  . Базисні невідомі:
. Базисні невідомі:  ; вільні невідомі:
; вільні невідомі: 
Розв'язуємо систему відносно базисних невідомих:

Так як  , то
, то

Запишемо цільову функцію z через вільні невідомі
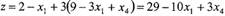
Отже, задача, рівносильна вихідній, має вигляд:

Із лем 1, 2 випливає така теорема.
Теорема 1. Основна задача лінійного програмування у першій стандартній формі і основна задача лінійного програмування у другій стандартній формі еквівалентні між собою
Економічна модель задачі
Фірма спеціалізується на виготовленні та реалізації електроплит і морозильних камер. Припустимо, що збут продукції необмежений, проте обсяги ресурсів (праці та основних матеріалів) обмежені. Завдання полягає у визначенні такого плану виробництва продукції на місяць, за якого виручка була б найбільшою.
Норми використання ресурсів та їх загальний запас, а також ціни одиниці кожного виду продукції наведені в табл. 1.
Таблиця 1 Інформація, необхідна для складання виробничої програми
| Вид продукції | Норми витрат на одиницю продукції | Ціна одиниці продукції, ум. од. | ||
| робочого часу, люд.-год. | листового заліза, м2 | скла, м2 | ||
| Морозильна камера | 9,2 | 3 | — | 300 |
| Електрична плита | 4 | 6 | 2 | 200 |
| Загальний запас ресурсу на місяць | 520 | 240 | 40 | — |
Побудуємо економіко-математичну модель даної задачі.
Позначимо через  кількість вироблених морозильних камер, а через,
кількість вироблених морозильних камер, а через,  — електроплит. Виразимо математично умови, що обмежують використання ресурсів.
— електроплит. Виразимо математично умови, що обмежують використання ресурсів.
Виходячи з нормативів використання кожного з ресурсів на одиницю продукції, що наведені в табл. 1, запишемо сумарні витрати робочого часу:
 .
.
За умовою задачі ця величина
не може перевищувати загальний запас даного ресурсу, тобто 520 люд.-год. Ця вимога описується такою нерівністю:

Аналогічно запишемо умови щодо використання листового заліза та скла:

Необхідно серед множини всіх можливих значень  та
та  знайти такі, за яких сума виручки максимальна, тобто: max
знайти такі, за яких сума виручки максимальна, тобто: max 
Отже, умови задачі, описані в прикладі 1.1, можна подати такою економіко-математичною моделлю:
 5
5
за умов:

Остання умова фіксує неможливість набуття змінними від'ємних значень, тому що кількість виробленої продукції не може бути від'ємною. Розв'язавши задачу відповідним методом математичного програмування, дістаємо такий розв'язок: для максимальної виручки від реалізації продукції необхідно виготовляти морозильних камер — 50 штук, електроплит — 15 (  =50,
=50, 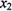 =15).
=15).
Перевіримо виконання умов задачі:
9,2-50 + 4·15 = 520;
3-50 + 6·15 = 240;
2·15 = 30<40.
Всі умови задачі виконуються, до того ж оптимальний план дає змогу повністю використати два види ресурсів з мінімальним надлишком третього.
Виручка становитиме: F = 300-50 + 200-15 = 18000 ум. од.
Отриманий оптимальний план у порівнянні з першим варіантом виробничої програми уможливлює збільшення виручки на
18000-16 800 = 1200 ум. од., тобто на 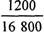 100% = 7,1%
100% = 7,1%
Математична модель задачі
Математична модель стандартної задачі – це її спрощений образ, поданий у вигляді сукупності математичних співвідношень (нерівностей). Загальна задача лінійного програмування (ЛП) подається у вигляді:
знайти максимум (мінімум) функції
 (29)
(29)
або 
за умов
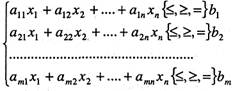 (30)
(30)
 (31)
(31)
Отже, потрібно знайти значення змінних  , які задовольняють умови (30) і (31), тоді як цільова функція набуває екстремального (максимального чи мінімального) значення.
, які задовольняють умови (30) і (31), тоді як цільова функція набуває екстремального (максимального чи мінімального) значення.
Задачу (29)—(2.3) легко звести до канонічної форми, тобто до такого вигляду, коли в системі обмежень (30) всі  (і =1,2, ...... n) невід'ємні, а всі обмеження є рівностями.
(і =1,2, ...... n) невід'ємні, а всі обмеження є рівностями.
Якщо якесь  від'ємне, то, помноживши
від'ємне, то, помноживши  -те обмеження на (—1), дістанемо у правій частині відповідної рівності додатне значення. Коли i-те обмеження має вигляд нерівності ,
-те обмеження на (—1), дістанемо у правій частині відповідної рівності додатне значення. Коли i-те обмеження має вигляд нерівності , 
 , то останню завжди можна звести до рівності, увівши допоміжну змінну
, то останню завжди можна звести до рівності, увівши допоміжну змінну

Аналогічно обмеження виду 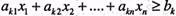 зводимо до рівності, віднімаючи від лівої частини допоміжну змінну
зводимо до рівності, віднімаючи від лівої частини допоміжну змінну  ,тобто І
,тобто І 
Приклад 2.1. Записати в канонічній формі таку задачу ЛП:

за умов
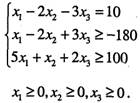
Розв'язування. Помножимо другу нерівність на (-1) і введемо відповідно допоміжні змінні 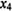 і
і  для другого та третього обмеження:
для другого та третього обмеження:

Неважко переконатися, що допоміжні змінні, у цьому разі  і
і  , є невід'ємними, причому їх уведення не змінює цільової функції.
, є невід'ємними, причому їх уведення не змінює цільової функції.
Отже, будь-яку задачу ЛП можна записати в такій канонічній формі:
знайти максимум функції  (32)
(32)
за умов
 (33)
(33)
 (34)
(34)
Задачу (32)—(34) можна розв'язувати на мінімум, якщо цільову функцію помножити на (-1), тобто

Дата добавления: 2019-07-15; просмотров: 671; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
