Виды математических моделей двойственных задач

Стр 1 из 3Следующая ⇒

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ДАГЕСТАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

ФАКУЛЬТЕТ МАГИСТРЕСКОЙ ПОДГОТОВКИ

Кафедра «Экономическая безопасность, налогообложение и бизнес-информатика»

Курсовая работа

По дисциплине «Математическое моделирование»

на тему:

«Экономический смысл двойственной задачи линейного программирования»

Выполнил: студент 1 курса, гр. И841 Хамидов З.Х.

Проверил: Ханов Р.Р.

Махачкала 2019г.

Студента 1 курса, гр. И 841

Хамидовава З.Х.

Руководитель:

к.э.н., ст. преподаватель

кафедры «ЭБНиБИ» Ханов Р.Р.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФГБОУ ВО ДАГЕСТАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА «ЭКОНОМИЧЕСКАЯ БЕЗОПАСНОСТЬ, НАЛОГООБЛОЖЕНИЕ И БИЗНЕС-ИНФОРМАТИКА»

ЗАДАНИЕ НА КУРСОВОЙ ПРОЕКТ (РАБОТУ)

Студент ____________________________ курс ______ группа __________

1. Тема ________________________________________________________

________________________________________________________________

2. Срок предоставления проекта (работы) к защите ________________________________________________________________

3. Исходные данные для проектирования (научного исследования)

________________________________________________________________

4. Содержание пояснительной записки курсового проекта (работы)

4.1. ____________________________________________________________

4.2. ____________________________________________________________

4.3. ____________________________________________________________

4.4. ____________________________________________________________

4.5. ____________________________________________________________

5. Перечень графического материала _______________________________

________________________________________________________________

Руководитель работы (подпись, Ф.И.О.) ___________ /_______________ /

Задание принял (подпись, Ф.И.О) _____________ / __________________ /

«____» ______________ 2019г.

Календарный план

№ п/п	Этапы работ	Сроки	Примечание
1.	Выбор темы и согласование с руководителем	16.03.2019
2.	Согласование плана и объекта работы	30.03.2019
3.	Сбор материала для курсовой работы
4.	Обработка материала
5.	Изучение литературы по теме работы
6.	Написание введения и первой главы
7.	Написание второй главы
8.	Написание третьей главы и заключения
9.	Оформление работы
10.	Представление работы руководителю
11.	Защита курсовой работы

Оглавление

Глава 1 Двойственность в линейном программировании

1.1 Прямые и двойственные задачи линейного программирования

1.2 Виды математических моделей двойственных задач

1.3 Двойственный симплексный метод

Глава 2 Двойственная задача линейного программирования

2.1 Основы теоремы двойственности

2.1.1 Несимметричные двойственные задачи

2.1.2 Симметричные двойственные задачи

2.2 Решение двойственной задачи линейного программирования

1.1.

Введение

Под двойственной задачей понимается вспомогательная задача линейного программирования, формулируемая с помощью определённых правил непосредственно из условий прямой задачи. Заинтересованность в определении оптимального решения прямой задачи путём решения двойственной к ней задачи обусловлена тем, что вычисления при решении двойственной задачи могут оказаться менее сложными. Трудоёмкость вычислений при решении задач линейного программирования в большей степени зависит от числа ограничений, а не от количества переменных.

Предмет исследования - экономический смысл двойственной задачи линейного программирования.

Целью курсового проекта является:

1. изучить литературу по выбранной теме

2. научиться применять на практике симплекс – метод для решения прямой и двойственной задачи линейного программирования

3. решить двойственную задачу линейного программирования с помощью программы MS Excel.

Настоящий курсовой проект состоит из введения, двух глав, включающих в себя семь параграфов, заключения и списка используемой литературы.

В первой главе рассматриваются основные понятия и предложения теории двойственности задач линейного программирования, виды математических моделей двойственных задач и их экономическая интерпретация.

Во второй главе рассматриваются основы теоремы двойственности, несимметричные и симметричные двойственные задачи, а также составление математической модели и решение двойственной задачи линейного программирования с помощью программы MS Excel.

Глава 1. Двойственность в линейном программировании.

Прямые и двойственные задачи линейного программирования

С экономической точки зрения двойственную задачу можно интерпретировать так: какова должна быть цена единицы каждого из ресурсов, чтобы при заданных количествах ресурсов bi и величинах стоимости единицы продукции Cj минимизировать общую стоимость затрат? А исходную задачу определим следующим, образом: сколько и какой продукции xj(j =1,2,…, n) необходимо произвести, чтобы при заданных стоимостях Cj (j=1,2,…, n) единицы продукции и размерах имеющихся ресурсов bi(i=1,2,…, n) максимизировать выпуск продукции в стоимостном выражении. Большинство задач линейного программирования изначально определяются как исходные или двойственные задачи. Сделав вывод можно говорить о паре двойственных задач линейного программирования.

Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу (линейного программирования), называемую двойственной или сопряженной по отношению к исходной или прямой задаче. Дадим определение двойственной задачи по отношению к общей задаче линейного программирования, состоящей, как мы уже знаем, в нахождении максимального значения функции:

F=c1x1+c2x2+…cnxn

при условиях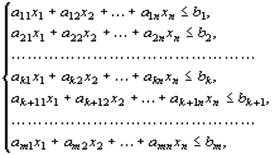

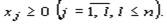
Сравнивая две сформулированные задачи, видим, что двойственная задача составляется согласно следующим правилам:

1. Целевая функция исходной задачи задается на максимум, а целевая функция двойственной на минимум.

2. Матрица

составленная из коэффициентов при неизвестных в системе ограничений исходной задачи, и аналогичная матрица

в двойственной задаче получаются друг из друга транспонированием (т.е. заменой строк столбцами, а столбцов – строками).

3. Число переменных в двойственной задаче равно числу ограничений в системе исходной задачи, а число ограничений в системе двойственной задачи – числу переменных в исходной задаче.

4. Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе исходной задачи, а правыми частями в соотношениях системы двойственной задачи – коэффициенты при неизвестных в целевой функции исходной задачи.

5. Если переменная xj исходной задачи может принимать только лишь положительные значения, то j-е условие в системе двойственной задачи является неравенством вида «>». Если же переменная xj может принимать как положительные, так и отрицательные значения, то 1 – соотношение в системе представляет собой уравнение. Аналогичные связи имеют место между ограничениями исходной задачи и переменными двойственной задачи. Если i – соотношение в системе исходной задачи является неравенством, то i-я переменная двойственной задачи 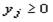. В противном случае переменная уj может принимать как положительные, так и отрицательные значения.

Двойственные пары задач обычно подразделяют на симметричные и несимметричные. В симметричной паре двойственных задач ограничения прямой задачи и соотношения двойственной задачи являются неравенствами вида « 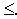«. Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.

Двойственная задача тесно связана задачей линейного программирования. Задача первоначальная называется исходной. Решение двойственной задачи может быть получено из решения исходной и наоборот. Связующим фактом этих двух задач являются коэффициенты Cj функции исходной задачи. Данные коэффициенты называются свободными членами системы ограничений двойственной задачи. Коэффициенты Bi системы ограничений исходной задачи называются коэффициентами двойственной задачи. Транспонированная матрица коэффициентов системы ограничений исходной задачи является матрицей коэффициентов системы ограничений двойственной задачи.

Рассмотрим задачу использования ресурсов. У предприятия есть t видов ресурсов в количестве bi (i=1, 2,…, m) единиц, из которых выпускается n видов продукции. На изготовление 1 ед. i-й продукции тратится aij ед. t-гo ресурса, ее стоимость составляет Cj ед. Необходимо определить план выпуска продукции, обеспечивающий ее максимальный выпуск в стоимостном выражении. Примем за xj (j=1,2,…, n) количество ед. j-й продукций и составляет максимальное значение линейной функции

Z=C1x1+C2x2+ … +Cnxn

Определим ресурсы, которые потребуются для изготовления товара. Обозначим за единицу стоимости ресурсов единицу стоимости выпускаемого товара. А через уi (j=1,2,…, m) стоимость единицы i-го ресурса. Т.е. стоимость всех затраченных ресурсов, которые используются для изобретения единицы j-й продукции, составляет. Цена израсходованных ресурсов не должна превышать цены окончательного товара.

Виды математических моделей двойственных задач

Основываясь на рассмотренных несимметричных и симметричных двойственных задач отметим, что пары двойственных задач математических моделей могут быть представлены следующим образом:

· Симметричные задачи

(1) Исходная задача Двойственная задача

Zmin=CX; fmax =Y>A0;

AX=A0; YA=С

X>0 Y>0

(2) Исходная задача Двойственная задача

Zmax =CX; fmin =YA0;

AX=A0; YA=С

X>0 Y>0

· Несимметричные задачи

(3) Исходная задача Двойственная задача

Zmin=CX; fmax=YA0;

AX=A0; YA=С

X>0

(4) Исходная задача Двойственная задача

Zmax=CX; fmin=YA0;

AX=A0; YA=С

X>0

Поэтому до того, как сформулировать двойственную задачу для данной исходной, необходимо систему ограничений исходной задачи преобразовать должным образом.

Дата добавления: 2019-07-15; просмотров: 421; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!