Несобственные интегралы 1-го и 2-го ряда.
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:
1) Область интегрирования является бесконечной. Например, является бесконечным промежутком {\displaystyle [a,+\infty )} [a,+\infty).
2) Функция f(x) является неограниченной в окрестности некоторых точек области интегрирования.
Если интервал [a,b] конечный и функция интегрируема по Риману, то значение несобственного интеграла совпадает со значением определённого интеграла.
Несобственный интеграл 1 рода возникает, когда по крайней мере одно из чисел a,b бесконечно.
Определение. Пусть существует конечный предел
A=limI(N)=lim∫Naf(x)dx.
N→+∞ N→+∞
Тогда говорят, что несобственный интеграл 1 рода (19) является сходящимся и ему приписывают значение A, саму функцию называют интегрируемой на интервале [a,+∞). Если же указанного предела не существует или он равен ±∞, то говорят, что интеграл (19) расходится.
Несобственные интегралы второго рода
Пусть b есть особая точка функции f(x) и для любого 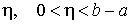 эта функция интегрируема на отрезке
эта функция интегрируема на отрезке 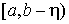 . Тогда предел
. Тогда предел
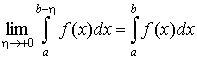 называется несобственным интегралом второго рода. Если этот предел существует и конечен, то говорят, что интеграл сходится или существует, если же этот предел равен бесконечности, то интеграл расходится, или не существует.
называется несобственным интегралом второго рода. Если этот предел существует и конечен, то говорят, что интеграл сходится или существует, если же этот предел равен бесконечности, то интеграл расходится, или не существует.
30) Некоторые специальные интегралы: интеграл Пуассона, Дирихле, Френеля. Понятие комплексных чисел, знакомство с теорией функций комплексного переменного.( Света)
|
|
|
31) Вычисление несобственных интегралов от степенной функции.

32) Признаки сходимости несобственных интегралов (признак сравнения, абсолютный, признак сравнения в предельной форме, признаки Абеля и Дирихле). Абсолютная и условная сходимость
Интегралы первого рода


Интегралы второго рода

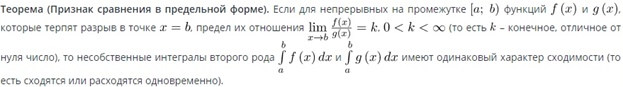
Абсолютная сходимость
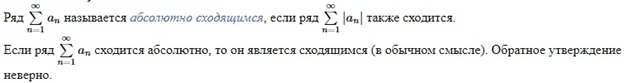
Признак Дирихле

Признак Абеля


33) Задачи линейной и нелинейной оптимизации. Формулировка. ( Света)
34) Понятие функции многих переменных (ФМП). График функции двух переменных.. Линия (поверхности) уровня. Область определения функции.
ФМП- это правило, при котором каждому х=(х1, х2, ….,хn) Î DfÎR^n поставлено в соответствии действительное число f( x )= f( x1, x2, …,xn) f: R^n ® R f: Af® Ef ( По Прилепкиной)
Если каждой точке множества D ставится в соответствие единственное число у из I, то говорят, что задана функция n переменных у=f(x1, …, xn). ( по интернету)
Графиком функции двух переменных z=f(x, y) называется множество точек (х, у, z) 3-мерного пространства, таких, что (х, у)ÎD(z) и z=f(x, y).
|
|
|
| Y |
| X |
| Z |
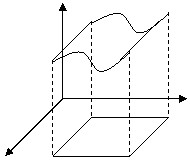
Линией уровня функции двух переменных называется линия на плоскости XOY, принадлежащая D(z), в каждой точке которой функция принимает одно и то же значение.
Уравнение линии уровня: f(x, y)=c, где с - произвольное число.
| =C |
| Z=1/9 |
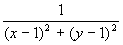
| Z=9 |
| Z=4 |
| Z=1 |
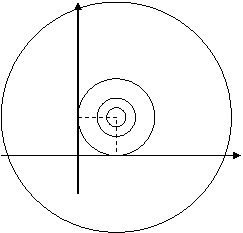
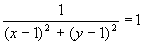 С=1 Z=1;
С=1 Z=1; 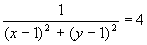 C=4 Z=4
C=4 Z=4
Область определения функции- это множество чисел на котором задается функция
35) Понятие кривой и ее носителя. Вектор скорости движения точки по кривой.
Понятие вектор-функции.
Опр. Непрерывное отображение отрезка [a, b] в пространство R3 называется кривой и обозначается Γ.
Опр. Множество точек пространства R3, на которое отображается отрезок [a, b], называется носителем кривой Γ.
В общем случае криволинейного движения вектор скорости может изменяться как по величине, так и по направлению. Рассмотрим характер этих изменений.
Пусть материальная точка, имевшая в положении A скорость υ и радиус-вектор r, за небольшой интервал времени ∆t совершила перемещение ∆rr и оказалась в точке B, положение которой определяется радиусом-вектором r1 (рис. 3.2). При этом ее скорость изменилась как по величине, так и по направлению, и определяется вектором υ1 .
|
|
|
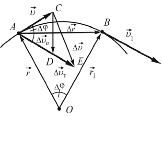 Изменение направления вектора скорости за время ∆t характеризуется углом поворота ∆φ , которому соответствует отрезок CD перемещения конца вектора v при повороте (∆υn=CD). Заметим, что радиус-вектор r также поворачивается на угол ∆φ, которому соответствует перемещение ∆r.
Изменение направления вектора скорости за время ∆t характеризуется углом поворота ∆φ , которому соответствует отрезок CD перемещения конца вектора v при повороте (∆υn=CD). Заметим, что радиус-вектор r также поворачивается на угол ∆φ, которому соответствует перемещение ∆r.
ВЕКТОР-ФУНКЦИЯ, векторная функция - функция r(t) аргумента t, значения которой принадлежат некоторому векторному пространству V.
В конечномерном (размерности m) векторном пространстве V задание вектор-функции эквивалентно заданию ее координат rj(t), 1 ≤ j ≤ m, в некотором базисе
е1, ..., еm пространства V:
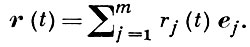
Вектор-функция называется непрерывной, дифференцируемой и т. п. (в точке или в области), если такими являются все функции rj(t).
36) Евклидово пространство.

37) Определение дифференцируемости ФМП. Уравнение касательной плоскости и нормали.
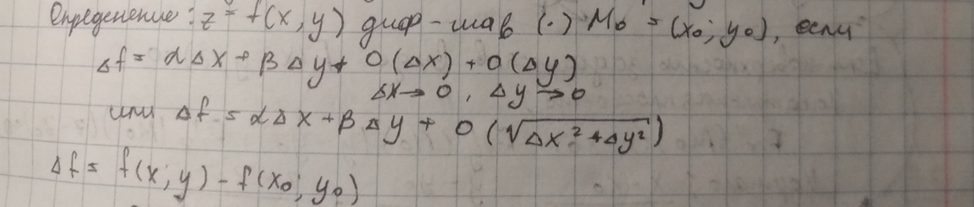
Определение.Касательной плоскостьью к поверхности z = f(x,y) в точке P0(x0,y0,f(x0,y0)) называется плоскость, содержащие все касательные к поверхности, проведённые в точке P0.
Определение.Нормалью к поверхности в точке P называется прямая, проходящая через эту точку перпендикулярно касательной плоскости, проведённой через точку P
|
|
|
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y), в точке M0(x0,y0,z0) имеет вид: z – z0 = f’x(x0,y0)(x – x0) + f’y(x0,y0)(y – y0)
Канонические уравнения нормали к поверхности, заданной уравнением z = f(x,y), в точке M0(x0,y0,z0), где z0 = f(x0,y0), имеют вид:
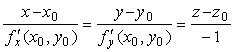
В случае, когда уравнение гладкой поверхности задано в неявном виде: F(x; y; z) = 0 и F(x0; y0; z0) = 0, то уравнение касательной плоскости в точке M0(x0; y0; z0) имеет вид
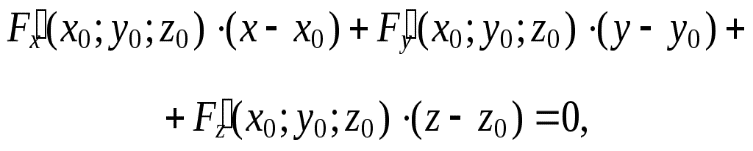 (3)
(3)
а уравнение нормали
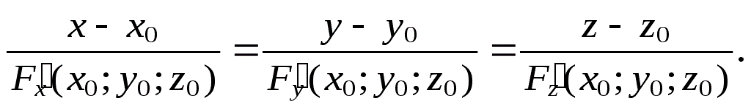
38) Дифференцирование сложной функции (ФМП). Доказательство.
Теорема. Пусть u = f (х, у) задана в области D и пусть х = х(t ) и у = у(t ) определены в области 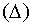 ,причём, когда
,причём, когда 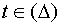 , то х и у принадлежат области D . Пусть функция u дифференцируема в точке M0(x0, y0, z0), а функции х(t ) и у(t ) дифференцируемы в соответствующей точке t0, то сложная функция u = f [x(t), y(t)]=F (t) дифференцируема в точке t0 и имеет место равенство:
, то х и у принадлежат области D . Пусть функция u дифференцируема в точке M0(x0, y0, z0), а функции х(t ) и у(t ) дифференцируемы в соответствующей точке t0, то сложная функция u = f [x(t), y(t)]=F (t) дифференцируема в точке t0 и имеет место равенство:
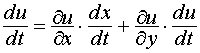 .
.
Доказательство. Так как u дифференцируема по условию в точке (x0, y0), то её полное приращение представляется в виде
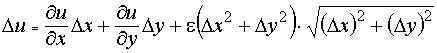 .Разделив это соотношение на
.Разделив это соотношение на 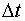 , получим:
, получим:
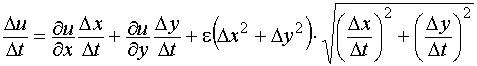 .
.
Перейдём к пределу при 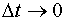 и получим формулу
и получим формулу 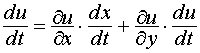 .
.
39) Частные производные. Дифференциал. Градиент, производная по направлению. Доказательство формулы вычисления производной по направлению. Смысл градиента.


40) Частные производные высших порядков. Теорема о равенстве смешанных производных.
Производные высших порядков.
Пусть дана дифференцируемая функция n переменных u( 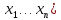 . Пусть также вычислена производная первого порядка по переменной
. Пусть также вычислена производная первого порядка по переменной 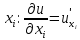 . Эта функция тоже зависит от переменных
. Эта функция тоже зависит от переменных 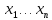 .
.
Возьмем от 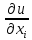 производную по переменной
производную по переменной 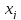 :
: 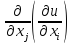 =
= 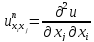 .
.
Функция 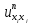 называется частной производной второго порядка от функции u(
называется частной производной второго порядка от функции u( 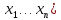 по переменным
по переменным 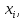
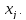 Таким же образом можно определить производные и третьего порядка .
Таким же образом можно определить производные и третьего порядка .
Таким образом, справедлива рекуррентная формула 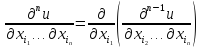 .
.
Производная 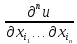 называется смешанной, если среди переменных
называется смешанной, если среди переменных 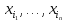 есть несовпадающие.
есть несовпадающие.
Пример. Рассмотрим функцию двух переменных 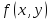 . Производные
. Производные 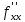 ,
, 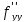 являются несмешанными производными,
являются несмешанными производными, 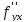 ,
, 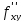 - смешанными производными.
- смешанными производными.
Теорема (о равенстве смешанных производных).
Пусть: 1) функция 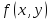 определена в некоторой окрестности точки
определена в некоторой окрестности точки 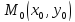 ;
;
2) существуют частные производные 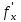 ,
, 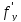 ,
, 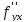 ,
, 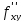 в этой окрестности;
в этой окрестности;
2) производные второго порядка 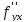 ,
, 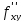 непрерывны в точке
непрерывны в точке 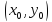 . Тогда
. Тогда 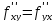 в точке
в точке 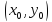 .
.
41) Формула Тейлора для ФМП.
Теорема. Пусть 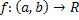 m+1 раз дифференцируемая функция ,
m+1 раз дифференцируемая функция , 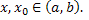 Тогда справедлива формула
Тогда справедлива формула
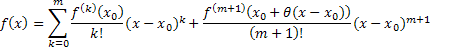 где
где 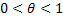 некоторое число.
некоторое число.
41) Понятие квадратичной формы. Критерий Сильвестра знакоопределенности квадратичных форм.

42) Исследование на экстремум функции многих переменных. Необходимое условие. Доказательство. Достаточное условие. Доказательство.

43) Условный экстремум. Метод множителей Лагранжа.
Дата добавления: 2019-07-15; просмотров: 187; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
