Метод замены переменной; Использование табличных формул; Метод подведения под знак дифференциала
Теоремы о точках экстремума.
•Если f — дважды дифференцируема в точке х=с и задана в окрестности х=с: f '(с)=0 и
f "(с)>0, то f имеет минимум (min) в точке с.
• Если f — дважды дифференцируема в точке х=с и задана в окрестности х=с, f ’ (с)=0 и
f "(с)<0, то f имеет максимум (шах) в точке с.
Необходимое и достаточные условия экстремума.
•Необходимое условие существования экстремума функции: если х = хо - точка экстремума, то f ‘(хо) =0 или f '(хо) не существует.
Точки, в которых f (хо) обращается в нуль или не существует, называется критическими. •Достаточное условие существования экстремума функции: если функция y=f(x) непрерывна в точке х = хо и ее окрестности, дифференцируема в этой окрестности (кроме, быть может, самой точки), и производная y'=f (х) при переходе через точку х = хо меняет свой знак, то функция имеет экстремум при х = хо
5) Понятие выпуклой функции. Точка перегиба, необходимое и достаточные условия.
6) Схема исследования функции и построения графика.
7) Дифференциал. Дифференциалы высших порядков. Формула Тейлора с остатком в форме Пеано.
8) Задача об эффективности рекламы. Понятие дифференциального уравнения первого порядка. (У Светы)
9) Понятие первообразной и точной первообразной. Нахождение первообразной от ступенчатой функции.
Определение первообразной функции
Функцию у= F ( x ) называют первообразной для функции у= f ( x ) на заданном промежутке Х, если для всех х ∈ Х выполняется равенство: F ′( x ) = f ( x )
|
|
|
Свойство первообразных
· Если F ( x ) — первообразная для функции f ( x ) на заданном промежутке, то функция f(x) имеет бесконечно много первообразных, и все эти первообразные можно записать в виде F ( x ) + С, где С — произвольная постоянная.
10) Теорема о множестве первообразных. Доказательство.
[Если F ( x ) – какая-нибудь первообразная от функции f ( x ) на интервале ( a , b ), то все ее первообразные имеют вид F ( x ) + С, где С – произвольная постоянная.]
Любые две первообразные f ( x ) отличаются только на константу F ( x ), С( x ) – первообразная. f ( x ) à F ( x )= G ( x )+ C
Доказательство. Пусть G(x) – одна из первообразных от функции f(x) на интервале (a , b), а F(х) – любая другая ее первообразная. Покажем, что функция H(х) = F(х) – G(x) постоянна на интервале (a , b ):
H ’(x) = F ’(x) – G ’(x) = f(x) – f(x) = 0, H ’(x) = 0. Зафиксируем точку х0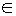 
(a , x), и пусть этолюбая точка из интервала (a , x). Запишем теорему Лагранжа о среднем для функции H(х):H(х) - H(a) = H ’(c)×(x - a) = 0
Т.к H’(c) = H’(x) = 0. Отсюда H(х) = H(a) = С, т. е. F(х) - G(x) = C , F(х) = G(x) + C .
11) Неопределенный интеграл. Таблица интегралов. Проверка некоторых формул дифференцированием.
Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается 
. Выражение 
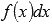называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).
|
|
|
Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.
Основные свойства неопределенного интеграла
1. Производная неопределенного интеграла равна подинтегральной функции: 
2. Дифференциал неопределенного интеграла равен подинтегральному выражению: 
3. Неопределенный интеграл от дифференциала некоторой функции равен сумме самой этой функции и произвольной постоянной: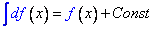 
4. Постоянный множитель можно выносить за знак интеграла: 
, причем 
5. Интеграл суммы (разности) равен сумме (разности) интегралов: 
6. Свойство является комбинацией свойств 4 и 5: 
, причем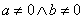 
7. Свойство инвариантности неопределенного интеграла: Если 
, то 
8. Свойство: Если , то
Проверка некоторых формул дифференцированием. Результат интегрирования проверим дифференцированием. Для этого найдем производную
Таким образом, производная от неопределенного интеграла равна подынтегральной функции, следовательно, интеграл от данной функции найден, верно.
|
|
|
11) Формула замены переменных. Доказательство. Занесение под дифференциал. Интеграл от линейной зависимости.
Теорема. Пусть функции 
и 
определены на промежутках 
и 
соответственно, причем 
, т. е. все значения функции 
принадлежат .
Если функция 
имеет на первообразную 
, а функция дифференцируема на , то следующая функция 
имеет на первообразную 
и при этом выполняется равенство: 
Доказательство. Т.к. все значения 
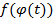, то на определены сложные функции 
и . Далее, т.к. - первообразная функции на , то 
, 
. Учитывая, что по условию функция 
также дифференцируема на . Тогда по теореме о дифференцируемости сложной функции
можно найти производную от функции: 
Последнее означает, что: является первообразной функции 
на 
.
Таким образом, 
С другой стороны, по теореме об общем виде первообразной: 
Подставим в него вместо 
: 
Учитывая, что 
и 
равны правые части, то левые части тоже равны: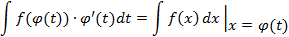 
Пусть требуется найти неопределенный интеграл ∫f(x)dx. Предположим,что существуют дифференцируемые функции u=ϕ(x) и v=g(u) такие, что f(x)dx=g(ϕ(x))dϕ(x)=g(ϕ(x))ϕ′(x)dx=g(u)du. Тогда ∫f(x)dx=∫g(ϕ(x))ϕ′(x)dx=∫g(u)du
|
|
|
Указанное преобразование подынтегрального выражения называют подведением под знак дифференциала.
Тогда, если ∫f(x)dx=F(x)+C и u=ϕ(x), то имеет место следующее равенство: ∫f(u)du=F(u)+C
12)
13) Интегрирование по частям. Доказательство.
14) Интегрирование рациональных функций. Сведение интеграла от неправильной дроби к интегралу от правильной дроби.
15) Метод неопределенных коэффициентов.
16) Интегрирование правильных дробей. Типы простых дробей и интегралы от них. (у меня)
17) Конструкция определенного интеграла на примерах: вычисление объема продукции, нахождение площади.
Вычисление площади: 
18) Определение определенного интеграла, разбиения, размеченного разбиения, интегральной суммы Римана, верхней и нижней сумм Дарбу.
Определенный интеграл – это предел интегральной суммы 
(Ci)∆Xi, где ∆Xi=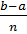 
2) Разбиением отрезка [ a ; b ] называется набор чисел Х0,…, Хn, такой что а=Х0<X1<X2<…<Xn=b
3) Размеченное разбиение отрезка [ a ; b ] Т: Х0<X1<X2<…<Xn=bк 
к Ꞓ[Xk+1,Xk], k=1,2,…,n
4) Интегральная сумма Римана. 
[a;b](f;v)= (εi) ∆Xi; 
= 
5) Mi=sup f(x), xꞒ[Xi-1;Xi], 
(T)= 
∆Xi верхняя грань
mi=inf f(x), xꞒ[Xi-1;Xi], 
(T)= 
∆Xi нижняя грань
18)
19) 
Линейность интеграла Римана.
20) Пример неинтегрируемой функции (функция Дирихле). Необходимое условие интегрируемости. 
- функция Дирихле
Т - любое разбиение, S*(T) = ∑ Mi ∆ix = ∑∆ix, Mi = max f(x), x ∈ [xi-1; xi] , S*(T) = ∑ mi ∆ix = 0
mi = min f(x), x ∈ [xi-1; xi] ⇒не интегрируемо. Необходимое условие интегрируемости: Если f(x) интегрируемо по Риману [a; b], то она ограничена на [a; b].
21) Интегрирование тригонометрических функций. Универсальная подстановка, формулы понижения степени и другие приемы.
∫R(sinx, cosx)dx, где R – рациональная функция (Функция рациональная относительно как синуса, так и косинуса)
Универсальная тригонометрическая подстановка:
t = x/2, dx = 2dt/1+t2 , sin x = 2t/1+t2, cos x = (1-t2)/( 1+t2)
Интегрирование тригонометрических функций:
Использование тригонометрических формул
sin² x + cos² x = 1, tg x * ctg x = 1, tg x = sin x / cos x, ctg x = cos x / sin x, 1 + tg² x = 1 / cos² x
1 + ctg² x = 1 / sin², xsin² x = (1 - cos 2x) / 2, cos² x = (1 + cos 2x) / 2, tg²x = (1 / cos² x) – 1
cos 2x = cos² x - sin² x, cos 2x = 2cos² x – 1, cos 2x = 1 - 2sin² x, sin 2x = 2sin x * cos x
Использование свойств неопределенного интеграла (интеграл от суммы равен сумме интегралов и тд.);
Метод замены переменной; Использование табличных формул; Метод подведения под знак дифференциала
22) Вычисление среднего значения времени на производство единицы изделия.
t(x) – функция затрат времени на изготовление изделия (t=ax-b)
t(1) = a – время на изделие 1. b – коэфицент производства.
среднее время, затраченное на изготовления [x1,x2] – tср
23) Свойства определенного интеграла (аддитивность интеграла по множеству, интегрирование неравенств, оценка модуля интеграла). Доказательство.
24) Первая теорема о среднем. Ее модификация. Геометрический смысл. Доказательство.
Геом смысл: Для непрерывной неотрицательной функции f(x) теорема о среднем значениии утверждает существование прямоугольника с основанием b − a и высотой, равной значению функции f(x) в некоторой точке ξ О [a,b], площадь которого равна площади криволинейной трапеции
1 Теорема о среднем: Пусть функция {\displaystyle f(x)}f(x) интегрируема на отрезке {\displaystyle [a;b]}[a;b], и ограничена на нём числами m {\displaystyle m} и {\displaystyle M}M так, что m =< f(x) =<M{\displaystyle m\leq f(x)\leq M}. Тогда существует такое число Ню, что, m =< Ню =<M{\displaystyle m\leq f(x)\leq M}, что ∫abf(x)dx=μ(b−a)
Док-во: Из неравенства m≤f(x)≤M по свойству монотонности интеграла имеем: m(b−a)≤∫abf(x)dx≤M(b−a). Обозначив μ=1/(b−a)∫baf(x)dx, получим требуемое утверждение. Так определённое число μ называют средним значением функции f(x) на отрезке [a;b], откуда и название теоремы.{\displaystyle \mu }{\displaystyle m\leq \mu \leq M}
{\displaystyle \int \limits _{a}^{b}f(x)dx=\mu (b-a)}
25) Вторая теорема о среднем. Формулировка.
Если функция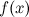 
интегрируема на отрезке 
, а функция 
монотонна на этом отрезке, то существует такая точка 
, что
Следствие 1. Если функция 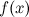интегрируема на отрезке , а функция является монотонно убывающей на этом отрезке и 
, тогда существует такая точка , что
Следствие 2. Если функция 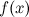интегрируема на отрезке , функция является монотонно возрастающей на рассматриваемом отрезке и , тогда существует такая точка , что
26) Интеграл с переменным верхним пределом. Теорема о его свойствах. Доказательство.
Непрерывность интеграла:
Дифференцируемость: Если функция ff интегрируема на отрезке [a,b][a,b] и непрерывна в точке x0∈[a,b]x0∈[a,b], то функция F(x)=∫axf(t)dtF(x)=∫axf(t)dt дифференцируема в точке x0x0, причем
F′(x0)=f(x0).(4). Доказательство:
27) Формула Ньютона-Лейбница. Доказательство.
Теорема. Если функция f(x) непрерывна на промежутке [a,b], то
| (1) |
где F(x) – первообразная функции f(x):
| (2) |
Формула (1) называется формулой Ньютона–Лейбница.
Доказательство. Сначала покажем, что функция
| (3) |
является первообразной функции f(x).
Согласно определению производной,
| (4) |
С учетом свойства 6,
| (5) |
Тогда
| (6) |
Применяя теорему о среднем к промежутку 
, представим интеграл в числителе в виде
| (7) |
где 
и 
при 
.
Следовательно,
| (8) |
Возвратимся к уравнению (3). Полагая x = a, находим значение постоянной C:
| (9) |
Полагая в этом же уравнении x = b, получаем:
 
| (10) |
Таким образом, для вычисления определенного интеграла от f(x) по промежутку [a,b] достаточно найти первообразную F(x) функции f(x), вычислить ее в точках a и b и вычесть F(a) из F(b).
28) Замена переменной и интегрирование по частям в определенном интеграле.
Замена переменной. Пусть 
-- дифференцируемое отображениеcнепрерывной производной и такое, что 
, а 
-- непрерывная функция, заданная на отрезке 
. Тогда
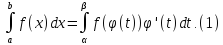
Доказательство. Пусть 
-- первообразная функции . Тогда по формуле замена переменной в неопределенном интеграле функция 
есть первообразная функции 
. Применим формулу Ньютона-Лейбница дважды:
-- что и требовалось доказать.
Интегрирование по частям. Пусть 
и 
-- дифференцируемые функции на отрезке . Тогда
Доказательство. Соотношение 
проинтегрируем от 
до 
b получим 
что эквивалентно (2).
29) Проблемы в определении интеграла Римана. Определение несобственных интегралов первого и второго рода.
Функция f называется интегрируемой по Риману на отрезке [a,b], если для любой последовательности разбиений 
, n = 1, 2, ...,
отрезка [a,b], мелкость которых стремится к нулю: 
| 
n| = 0 , и для любого выбора точек 
, k = 1, 2, ..., 
, последовательности интегральных сумм
, n = 1, 2, ...,
имеют и притом один и тот же предел.
Этот предел называется интегралом Римана функции f по отрезку [a,b]. Его обозначают 
и пишут
Дата добавления: 2019-07-15; просмотров: 299; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!