Формула интегрирования по частям определенного интеграла.
⇐ ПредыдущаяСтр 2 из 2
Пусть u и v - непрерывно дифференцируемые функции. Проинтегрируем равенство d(uv)=udv+vdu в пределах от a до b.
 |
В левой части применим формулу Ньютона-Лейбница:
Получим:
 |  |  |
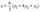 (2)
Доказательство. Подставляя в уравнение у=Ах2+Вх+С координаты точек М1, М2, М3, получаем у1=Аh2-Вh+С; у2=С; у3=Аh2+Вh+С, откуда следует, что
2Аh2+2С=у1+у3; С=у2 (3)
Учитывая соотношение (3), имеем
(2)
Доказательство. Подставляя в уравнение у=Ах2+Вх+С координаты точек М1, М2, М3, получаем у1=Аh2-Вh+С; у2=С; у3=Аh2+Вh+С, откуда следует, что
2Аh2+2С=у1+у3; С=у2 (3)
Учитывая соотношение (3), имеем
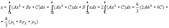 Рассмотрим снова криволинейную трапецию, ограниченную произвольной кривой y=f(x). Разобьем отрезок [a, b] на 2p равных отрезков точками a=x0<x1<x2<...<x2k<x2k+1<x2k+2<...<x2n-1<x2n=b, а кривую y=f(x) с помощью прямых x=xk на 2n соответствующих частей точками М0 , М1 , М2 , ..., М2k , М2k+1 , М2k+2, ..., М2n-2 , М2n-1 , М2n (рис. 3).
Через каждую тройку точек
М0 М1 М2 , ..., М2k М2k+1 М2k+2, ..., М2n-2 М2n-1 М2n
проведем кривую вида у=Ах2+Вх+С (см. лемму 1.1). В результате получим n криволинейных трапеций, ограниченных сверху параболами или прямыми (эти трапеции заштрихованы на рис. 3). Так как площадь частичной криволинейной трапеции, соответствующей отрезку [x2k, x2k+2], приближенно равна площади соответствующей “параболической” трапеции, то по формуле (2) имеем [в данном случае h=(b-a)/(2n)]
Рассмотрим снова криволинейную трапецию, ограниченную произвольной кривой y=f(x). Разобьем отрезок [a, b] на 2p равных отрезков точками a=x0<x1<x2<...<x2k<x2k+1<x2k+2<...<x2n-1<x2n=b, а кривую y=f(x) с помощью прямых x=xk на 2n соответствующих частей точками М0 , М1 , М2 , ..., М2k , М2k+1 , М2k+2, ..., М2n-2 , М2n-1 , М2n (рис. 3).
Через каждую тройку точек
М0 М1 М2 , ..., М2k М2k+1 М2k+2, ..., М2n-2 М2n-1 М2n
проведем кривую вида у=Ах2+Вх+С (см. лемму 1.1). В результате получим n криволинейных трапеций, ограниченных сверху параболами или прямыми (эти трапеции заштрихованы на рис. 3). Так как площадь частичной криволинейной трапеции, соответствующей отрезку [x2k, x2k+2], приближенно равна площади соответствующей “параболической” трапеции, то по формуле (2) имеем [в данном случае h=(b-a)/(2n)]
 где yk=f(xk), k=0, 1, 2, ...,2n. Складывая почленно эти приближенные равенства, получаем приближенную формулу
где yk=f(xk), k=0, 1, 2, ...,2n. Складывая почленно эти приближенные равенства, получаем приближенную формулу
 или в развернутом виде
или в развернутом виде
 Эта формула называется формулой парабол или формулой Симпсона.
30.Приближенное вычисление определенного интеграла. Формула трапеций.
Эта формула называется формулой парабол или формулой Симпсона.
30.Приближенное вычисление определенного интеграла. Формула трапеций.
 Пусть требуется вычислить интеграл
Пусть требуется вычислить интеграл  , где f(x) - непрерывная функция. Для простоты рассуждений ограничимся случаем, когда f(x)³ 0. Разобьем отрезок [a, b] на n отрезков точками a=x0<x1<x2<...<xk-1<xk<...<xn=b и с помощью прямых х=хk построим n прямолинейных трапеций (эти трапеции заштрихованы на рис. 1). Сумма площадей трапеций приближенно равна площади криволинейной трапеции, т.е.
Где f(xk-1) и f(xk) - соответственно основания трапеций; xk - xk-1 = (b-a)/n - их высоты.
Таким образом, получена приближенная формула
, где f(x) - непрерывная функция. Для простоты рассуждений ограничимся случаем, когда f(x)³ 0. Разобьем отрезок [a, b] на n отрезков точками a=x0<x1<x2<...<xk-1<xk<...<xn=b и с помощью прямых х=хk построим n прямолинейных трапеций (эти трапеции заштрихованы на рис. 1). Сумма площадей трапеций приближенно равна площади криволинейной трапеции, т.е.
Где f(xk-1) и f(xk) - соответственно основания трапеций; xk - xk-1 = (b-a)/n - их высоты.
Таким образом, получена приближенная формула
 которая и называется формулой трапеций. Эта формула тем точнее, чем больше n.
31.Несобственные интегралы с бесконечными пределами. +++32.Несобственные интегралы второго ряда.
Несобственными интегралами называются: 1) интегралы с бесконечными пределами; 2) интегралы от неограниченных функций. Несобственный интеграл от функции f(x) в пределах от a до +Ґ определяется равенством
которая и называется формулой трапеций. Эта формула тем точнее, чем больше n.
31.Несобственные интегралы с бесконечными пределами. +++32.Несобственные интегралы второго ряда.
Несобственными интегралами называются: 1) интегралы с бесконечными пределами; 2) интегралы от неограниченных функций. Несобственный интеграл от функции f(x) в пределах от a до +Ґ определяется равенством
 Если этот предел существует, то несобственный интеграл называется сходящимся; если же предел не существует, - расходящимся. Аналогично
Если этот предел существует, то несобственный интеграл называется сходящимся; если же предел не существует, - расходящимся. Аналогично
 и
и
 Если функция f(x) имеет бесконечный разрыв в точке с отрезка [a,b] и непрерывна при a <= x < с и с < x < b, то по определению, полагают
Если функция f(x) имеет бесконечный разрыв в точке с отрезка [a,b] и непрерывна при a <= x < с и с < x < b, то по определению, полагают

 Sn+1=Sn+an+1
Выражение
a1+a2+…+ а n +an+1+… (1)
обозначается символом
Sn+1=Sn+an+1
Выражение
a1+a2+…+ а n +an+1+… (1)
обозначается символом  и называется числовым рядом.
Числа а1, а2,…,а n,… называются членами ряда, а число аn- n – м членом или общим членом ряда.
Простейшие свойства числовых рядов
1о. Сходимость ряда не нарушится, если произвольным образом изменить (переставить, добавить или отбросить) конечное число членов ряда.
2о. Сходящийся ряд можно почленно умножить на любой множитель
и называется числовым рядом.
Числа а1, а2,…,а n,… называются членами ряда, а число аn- n – м членом или общим членом ряда.
Простейшие свойства числовых рядов
1о. Сходимость ряда не нарушится, если произвольным образом изменить (переставить, добавить или отбросить) конечное число членов ряда.
2о. Сходящийся ряд можно почленно умножить на любой множитель  , т.е. если ряд
, т.е. если ряд  имеет сумму S, то ряд
имеет сумму S, то ряд
 3о. Сходящиеся ряды можно почленно складывать и вычитать, т.е. если даны ряды
3о. Сходящиеся ряды можно почленно складывать и вычитать, т.е. если даны ряды
 то ряд
то ряд
 34.Необходимые условия сходимости ряда.
Теорема: Пусть числовой ряд
u1+u2+...+un+... , (1)
сходится, а S - его сумма. Тогда при неограниченном возрастании числа n членов ряда его общий член un стремится к нулю Доказательство. Из условия теоремы имеем
34.Необходимые условия сходимости ряда.
Теорема: Пусть числовой ряд
u1+u2+...+un+... , (1)
сходится, а S - его сумма. Тогда при неограниченном возрастании числа n членов ряда его общий член un стремится к нулю Доказательство. Из условия теоремы имеем

 Так как
Sn - Sn-1 = un
то
Так как
Sn - Sn-1 = un
то
 Следует отметить, что этот признак является лишь необходимым, но не достаточным признаком сходимости ряда, так как можно указать ряд, для которого выполняется равенство
Следует отметить, что этот признак является лишь необходимым, но не достаточным признаком сходимости ряда, так как можно указать ряд, для которого выполняется равенство
 ,
а он, однако не является сходящимся. Так гармонический ряд
,
а он, однако не является сходящимся. Так гармонический ряд
 ,
для которого
,
для которого
 ,
расходится. Но согласно доказанному необходимому признаку сходимости ряда, если
,
расходится. Но согласно доказанному необходимому признаку сходимости ряда, если
 ,
то ряд (1) расходится. В самом деле, если бы он сходился, то
,
то ряд (1) расходится. В самом деле, если бы он сходился, то
 равнялся бы нулю. Таким образом, доказанная нами теорема иногда позволяет, не вычисляя суммы Sn, сделать заключение о расходимости того или иного ряда. Например, ряд
равнялся бы нулю. Таким образом, доказанная нами теорема иногда позволяет, не вычисляя суммы Sn, сделать заключение о расходимости того или иного ряда. Например, ряд
 ,
расходится, так как
,
расходится, так как
 ,
35.Сходимость гармонического ряда.
-------( нету)
,
35.Сходимость гармонического ряда.
-------( нету)
 и
и  имеет место неравенство
имеет место неравенство
 (8)
n =1,2,…
Тогда:
1. Если сходится ряд
(8)
n =1,2,…
Тогда:
1. Если сходится ряд  , то сходится и ряд
, то сходится и ряд  2. Если расходится ряд
2. Если расходится ряд  , то расходится и ряд
, то расходится и ряд  .
Этот признак утверждает, что при выполнении условия (8) из сходимости ряда с большими членами вытекает сходимость ряда с меньшими членами, а из расходимости ряда с меньшими членами вытекает расходимость ряда с большими членами.
Теорема 2. (Предельный признак сравнения).
Пусть члены рядов
.
Этот признак утверждает, что при выполнении условия (8) из сходимости ряда с большими членами вытекает сходимость ряда с меньшими членами, а из расходимости ряда с меньшими членами вытекает расходимость ряда с большими членами.
Теорема 2. (Предельный признак сравнения).
Пусть члены рядов  и
и  положительны и
положительны и
 Тогда ряды
Тогда ряды  и
и  одновременно сходятся или одновременно расходятся.
37.Признак сравнения.
Пусть даны два ряда с полжительными членами.
одновременно сходятся или одновременно расходятся.
37.Признак сравнения.
Пусть даны два ряда с полжительными членами.  и
и  Причем, каждый член ряда
Причем, каждый член ряда  не превосходит соответствующего члена ряда
не превосходит соответствующего члена ряда  , то есть
, то есть  для всех
для всех  . Тогда
· если сходится ряд
. Тогда
· если сходится ряд  с большими членами, то сходится и ряд
с большими членами, то сходится и ряд  с меньшими членами;
· если расходится ряд
с меньшими членами;
· если расходится ряд  с меньшими членами, то расходится и ряд
с меньшими членами, то расходится и ряд  с большими членами.
Теорема остается верна, если соотношения между членами рядов выполняются не для всех
с большими членами.
Теорема остается верна, если соотношения между членами рядов выполняются не для всех  , а лишь начиная с некоторого номера
, а лишь начиная с некоторого номера  .
При использовании признаков сравнений чаще всего исследуемый ряд сравнивают с бесконечной геметрической пргрессией
.
При использовании признаков сравнений чаще всего исследуемый ряд сравнивают с бесконечной геметрической пргрессией  , которая сходится при
, которая сходится при  и расходится при
и расходится при  , или с рядом
, или с рядом  , который сходится при
, который сходится при  и расходится при
и расходится при  .
38.Признак Даламбера.
Пусть l - предел отношения последующего члена un+1 ряда (1) к предидущему un при n ® ¥ , т.е.
.
38.Признак Даламбера.
Пусть l - предел отношения последующего члена un+1 ряда (1) к предидущему un при n ® ¥ , т.е.
 Тогда, если l < 1, то ряд l сходится, если l > 1, то ряд l расходится, Если же l = 1, то вопрос о сходимости ряда (1) остается открытым. Доказательство. Согласно определению предела переменной величины, равенство
Тогда, если l < 1, то ряд l сходится, если l > 1, то ряд l расходится, Если же l = 1, то вопрос о сходимости ряда (1) остается открытым. Доказательство. Согласно определению предела переменной величины, равенство
 означает, что, начиная с некоторого номера n, выполняются неравенства
означает, что, начиная с некоторого номера n, выполняются неравенства
 где e - наперед заданное сколь угодно малое положительное число. Рассмотрим три случая: а) пусть l < 1 . Тогда всегда можно взять e настолько малым, чтобы выполнялось неравенство
l + e < 1
и, начиная с некоторого n , неравенство
где e - наперед заданное сколь угодно малое положительное число. Рассмотрим три случая: а) пусть l < 1 . Тогда всегда можно взять e настолько малым, чтобы выполнялось неравенство
l + e < 1
и, начиная с некоторого n , неравенство
 где q = l + e , в силу чего (см. теорему 1) ряд (1) будет сходящимся; б) пусть l > 1 . Выбираем e так, чтобы
e = l - 1 > 0
Тогда l - e = 1 и
где q = l + e , в силу чего (см. теорему 1) ряд (1) будет сходящимся; б) пусть l > 1 . Выбираем e так, чтобы
e = l - 1 > 0
Тогда l - e = 1 и
 т.е. ряд (1) расходится (см. теорему 1) в) пусть l = 1 . Тогда ряд (1) может быть как сходящимся, так и расходящимся. В самом деле, для гармонического ряда
т.е. ряд (1) расходится (см. теорему 1) в) пусть l = 1 . Тогда ряд (1) может быть как сходящимся, так и расходящимся. В самом деле, для гармонического ряда
 который расходится, имеем,
который расходится, имеем,
 С другой стороны, ряд
С другой стороны, ряд
 сходится, а для него также
сходится, а для него также
 потому что
потому что
 Таким образом, доказано, что если
то ряд (1) сходится; если l > 1 , то ряд (1) расходится.
39.Интегральный признак Коши.
Пусть
Таким образом, доказано, что если
то ряд (1) сходится; если l > 1 , то ряд (1) расходится.
39.Интегральный признак Коши.
Пусть  - непрерывная, неотрицательная, монотонно убывающая функция, определенная при
- непрерывная, неотрицательная, монотонно убывающая функция, определенная при  . Тогда ряд
. Тогда ряд  и интеграл
и интеграл  либо оба сходятся, либо оба расходятся.
Доказательство. Ввиду монотонности при всех
либо оба сходятся, либо оба расходятся.
Доказательство. Ввиду монотонности при всех  выполняются неравенства
выполняются неравенства  . Интегрируя, получаем
. Интегрируя, получаем  . Тогда
. Тогда  , или
, или  . Поэтому если
. Поэтому если 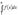 сходится, то
сходится, то  . Тогда
. Тогда 
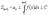 и
и  ,
,  ряд сходится.
Пусть теперь наоборот, известно, что ряд сходится. Тогда
ряд сходится.
Пусть теперь наоборот, известно, что ряд сходится. Тогда  . Взяв произвольное
. Взяв произвольное  выберем
выберем  так, чтобы
так, чтобы  . Тогда
. Тогда 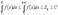 . Значит,
. Значит,  сходится.
40.Знакопеременные ряды.
Числовой ряд, члены которого имеют различные знаки, называется знакопеременным рядом.
Пусть дан знакопеременный ряд
сходится.
40.Знакопеременные ряды.
Числовой ряд, члены которого имеют различные знаки, называется знакопеременным рядом.
Пусть дан знакопеременный ряд
 . (1)
Рассмотрим ряд, составленный из модулей его членов:
. (1)
Рассмотрим ряд, составленный из модулей его членов:
 . (2)
Определение 1. Ряд (1) называется условно сходящимся, если сам ряд (1) сходится, а ряд (2), составленный из абсолютных величин, расходится.
Определение 2. Ряд (1) называется абсолютно сходящимся, если сам ряд (1) сходится и ряд из абсолютных величин тоже сходится.
Теорема. Если ряд, составленный из абсолютных величин членов знакопеременного ряда, сходится, то и сам ряд сходится (из абсолютной сходимости следует условная).
41.Знакочередующиеся ряды. Признак Лейбница.
Признак Лейбница.
Пусть дан знакочередующийся ряд
. (2)
Определение 1. Ряд (1) называется условно сходящимся, если сам ряд (1) сходится, а ряд (2), составленный из абсолютных величин, расходится.
Определение 2. Ряд (1) называется абсолютно сходящимся, если сам ряд (1) сходится и ряд из абсолютных величин тоже сходится.
Теорема. Если ряд, составленный из абсолютных величин членов знакопеременного ряда, сходится, то и сам ряд сходится (из абсолютной сходимости следует условная).
41.Знакочередующиеся ряды. Признак Лейбница.
Признак Лейбница.
Пусть дан знакочередующийся ряд
 (монотонно стремится к 0), тогда А сходится.
Доказательство.
(монотонно стремится к 0), тогда А сходится.
Доказательство.
 Т.к.
Т.к. 
 .
.
 ,
,  , то есть последовательность частичных сумм
, то есть последовательность частичных сумм  убывает, а
убывает, а  возрастает.
возрастает.
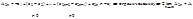 Каждая из последовательностей
Каждая из последовательностей  ограничена и
ограничена и  .
Следовательно,
.
Следовательно,  .
.

 Заметим, что:
Заметим, что:
 .
.
 42.Степенные ряды. Признак Абеля.
Признак Абеля.
Пусть дан ряд:
42.Степенные ряды. Признак Абеля.
Признак Абеля.
Пусть дан ряд:
 :
: 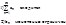
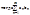 Доказательство.
Доказательство.
 Доказано.
43.Теорема об интервале сходимости степенного ряда.
44.Теорема о радиусе сходимости степенного ряда.
Доказано.
43.Теорема об интервале сходимости степенного ряда.
44.Теорема о радиусе сходимости степенного ряда.
|
|
|
Дата добавления: 2019-07-15; просмотров: 140; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
