Замена переменных в определенном интеграле.
Метод неопределенных коэффициентов.
1. Разложим знаменатель на множители:
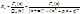
2. Правильная дробь разлагается в сумму простейших и каждому множителю вида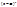 
соотв. сумма из n простейших дробей вида:
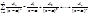с неопределенным коэф. A1 …n
Каждому множителю вида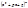 
соот. сумма из m простейших дробей вида: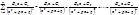 
с неопределенным коэф.B1 C1…
3. Неизвестный коэф. находится методом неопределенных коэф., основанном на: определении, что 2 многочлена тождественно совпадают, если у них равные коэффициенты при одинаковых степенях.
4. Приравнивая коэф. при одинаковых степенях в левой и правой частях, получим систему линейных уравнений относительно неизвестного уравнения.
Понятие интегральной суммы. Геометрический смысл.
Определение. Пусть непрерывная функция от одной переменной задана на отрезке [a, b].
1) Тогда разбиением отрезка [a, b] называется конечное множество точек х0 , х1 ... хn , где
а = х0 < х1< х2 < .... < хn-1 < хn = b
2) обозначим через D хi = хi – хi-1, i=1, 2, …, n
Диаметром разбиения называется
D = 
- длина максимального из отрезков разбиения.
На каждом отрезке 
, i = 1, 2, …, n, произвольно выберем 
и составим сумму
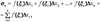(13)
которая называется интегральной суммой Римана функции f(х), соответствующей
данному разбиению отрезка [а, b] и выбору точек 
.
Теперь выясним геометрический смысл интегральных сумм Римана.
Пусть f (х) непрерывная на отрезке [а, b] функция, причем f (х) 
0, 
.
Произведение f( )Dхi равно заштрихованной площади прямоугольника с основанием D х= хi - хi-1 и высотой f ( ).
|
|
|
Тогда сумма
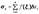
представляет собой сумму площадей n прямоугольников, с основаниями D хi и высотами f ( ), i = 1, 2…, n. Здесь х0=а, хn = b.
Если при стремлении к нулю диаметра разбиения отрезка [а, b] существует предел (14), то определенный интеграл представляет собой площадь криволинейный трапеции.
Свойства определенного интеграла.
Df. Промежуток с гранич. т. A и B ориентированным, если указано направление перехода от т. A к т. B.
1. Пусть сущ. определенный интеграл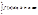 
сущ. определенный интеграл 
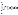и справедливо равенство
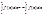
2. 
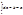
Док-во:
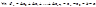
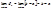
3. Свойство линейности определенного интеграла:
1. Пустьф-ии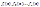 
интегрируемы на 
***
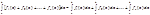
2. Пусть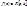 
, то для любой произвольной постоянной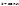 
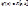- справедлива формула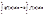 
4. Аддитивность определенного интеграла:
Пусть ф-ия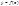 
интегрируема на большем их трех помежутков 
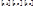, тогда она интегрируема на обоих меньших промежутках и справедлива формула:
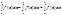Свойство монотонности.
1. Пусть ф-ия 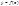неотрицательна на 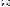и интегрируема на нем, 
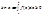Док-во: В силу н-ва для ф-ий любая интегрируема ф-ия неотрицательна Þ любая последовательность интегрируемых сумм будет иметь неотрицательный предел Þ интеграл будет неотрицательным.
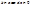
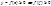2. Пусть ф-ия 
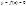на 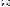, искл. конечн. точек, и интегрируема на 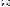, тогда 
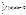Док-во: Из интегрируемости следует, что предел не зависит от выбора разбиения на 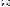. Достаточно строить инт. разбиения так, чтобы точки, в которых ф-ия равна нулю, являлись точками разбиения. А следовательно в силу аддитивности интеграл по всему прмежутку равен сумме интегралов по частичным промежуткам, т.к ****
Df Две ф-ии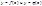 
, заданные на 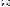, значения которых различны на 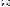лишь в конечном ч. точек называются эквивалентными на этом отрезке.
3. Инт. от эквивалентных ф-ий совп.
Пусть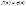 
эквивалентны и интегрируемы на 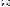, тогда 
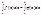(они не совпадают а интегралы совпадают).
Д-во:
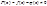на лишь в конеч. ч. точек отр. , следовательно по 2му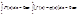 
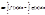4. Пусть 
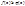на 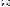, кроме конечного ч. точек, 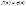инт. на , 
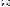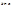, то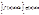 
5. Пусть 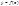инт-ма на 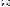Þ модуль ф-ии тоже интегрируем на 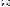и справедливо неравенство:
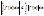6. Пусть 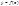интегрируема на 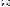, , 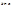то существует М, такая что 
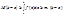25.Интеграл с переменным верхним пределом.
Теорема о его непрерывности.
Теорма: Если функция f ( x ) интегрируема на отрезке [a,b], то функция
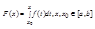непрерывна на этом отрезке.
Доказательство: Дадим числу х приращение ∆х так, чтобы х+∆х Î [ a , b ]. Для наглядности изобразим на числовой оси один из возможных вариантов расположения точек:
 |
|
|
|
|
|
|
 |
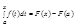a x 0 x х+∆х b
 |
 |
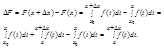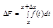Получим:
По теореме (Если функция y=f(x) интегрируема на отрезке, то интегрируема и абсолютная величина |f(x)|, причем
 |
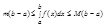…(на этом теорема закончилась, но неравенство относится к ней.) и следствию из теоремы (Если на отрезке [a,b] функция f(x) интегрируема и удовлетворяет неравенству m£f(x)£M. То выполняются неравенства:
(на этом следствие из теоремы закончилось)
получаем:
Отсюда следует, что при ∆х→0 будет ∆ F →0. Это доказывает непрерывность функции F ( x ). Отметим, что для подынтегральной функции f ( x ) точка х может быть точкой разрыва.
Формула Ньютона-Лейбница.
Пусть F(x) -произвольная первообразная для функции f(x), заданной на промежутке [a,b]. Так как две первообразные одной и той же функции отличаются на постоянное слагаемое, то верно равенство (1):
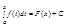
( в качестве числа х0 взято число а).
 |
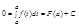В этом тождестве положим х=а и получим ,
Откуда С = -F(a). Формула (1) примет вид:
|
|
|
Заменяя здесь х на b, приходим к формуле Ньютона-Лейбница:
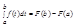
Иногда ее правую часть записывают короче с помощью двойной подстановки:
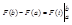
Замена переменных в определенном интеграле.
Теорема: при замене переменной х на t по формуле x = φ ( t ) равенство (1)
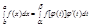
Справедливо при условиях:
1. φ(α) = а, φ(β) = b,
2. φ'(t) непрерывна на отрезке [α,β],
3 f(x) непрерывна на отрезке [a,b], а f[φ(t)] определена непрерывна на отрезке [α,β].
 |
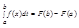Доказательство: при наших предположениях левая и правая части равенства (1) существуют и существуют первообразные подынтегральные функции. Пусть ∫f(x)dx = F(x)+C. Тогда, как легко проверить дифференцированием обеих частей, справедливо равенство ∫f[φ(t)]φ'(t)dt = F[φ(t)]+C правая часть дифференцируется как сложная функция). Применяем формулу Ньютона-Лейбница
Получаем
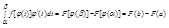
(по условию 1)
правые части этих двух равенств оказываются одинаковыми, следовательно, можно приравнять левые части. Приравнивая их, приходим к равенству (1). Ч.т.д.
Дата добавления: 2019-07-15; просмотров: 214; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!