Понятие базиса системы векторов
Определение. Базисом конечной системы векторов называется непустая линейно независимая подсистема, эквивалентная всей системе.
Теорема 1. Всякая конечная система векторов, содержащая хотя бы один ненулевой вектор, обладает базисом. Любые два базиса конечной системы векторов состоят из одинакового числа векторов.
Доказательство. Пусть дана конечная система векторов
. 
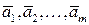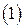
Предположим, что она содержит хотя бы один ненулевой вектор, например,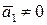 
. если система векторов 
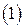состоит только из одного вектора , который отличен от нуля, то эта система является базисом.
Предположим, что 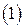состоит из 
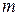векторов, где 
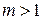. Здесь возможно два случая:
1) векторы системы - линейно независимы, значит, они образуют базис;
2) среди векторов системы 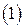есть хотя бы один вектор, который является линейной комбинацией остальных векторов системы 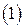, т.е. эта система линейно зависима.
Предположим, что среди векторов системы 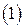вектор 
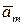есть линейная комбинация (л.к.) остальных векторов этой системы. Вычеркнем его из системы, и тогда получится новая система
. 
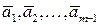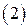
Рассмотрим систему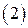 
. Возможны два случая:
1) Среди векторов системы 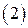нет таких векторов, которые бы являлись л.к. остальных, т.е. векторы линейно независимы. Значит, они образуют базис.
|
|
|
2) Система 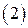линейно зависима. Значит, хотя бы один из векторов этой системы есть л.к. остальных векторов этой системы. Пусть это будет вектор 
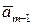. Вычеркнем его из системы 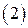и получим новую систему
. 
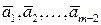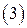
С системой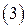 
поступаем далее так же, как и с системой 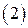. И, наконец, придем к такой системе векторов, которая будет являться линейно независимой подсистемой системы 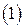, а, значит, будет базисом этой системы.
Покажем, что любые два базиса системы 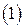состоят из одинакового числа векторов. В самом деле, пусть мы имеем два базиса системы :
, 
. 
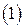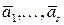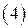
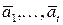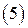
Тогда по второму следствию из определения эквивалентности двух систем, они состоят из одинакового числа векторов. Теорема доказана.
Ранг конечной системы векторов
Определение. Число векторов, входящих в базис конечномерной системы векторов называют рангом этой системы.
Теорема 1. Если система векторов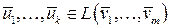 
, то ранг системы векторов 
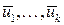не превосходит ранга системы векторов 
.
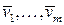Доказательство. Если все векторы системы векторов 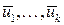нулевые, то теорема очевидна. Пусть хотя бы один из векторов системы ненулевой, тогда среди векторов 
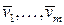есть ненулевые векторы. По теореме о базисе обе эти системы обладают базисами. Предположим, что система векторов 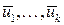обладает базисом 
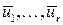. А система векторов 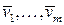обладает базисом 
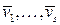. Ясно, что
|
|
|
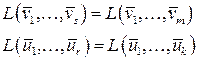
Значит,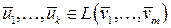 
, откуда следует, что 
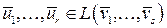. Поскольку векторы 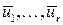образуют базис системы векторов 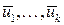, то они являются линейно независимыми. Значит, 
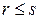. Теорема доказана.
Теорема 2. Ранг любой подсистемы конечной системы векторов не больше ранга всей системы векторов.
Доказательство непосредственно следует из теоремы 1.
Теорема 3. Эквивалентные конечные системы векторов имеют один и тот же ранг.
Доказательство непосредственно следует из теоремы 1.
Теорема 4. Ранг любой конечной системы векторов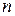 
-мерного арифметического векторного пространства не больше .
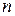Доказательство. Рассмотрим в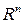 
систему векторов
.
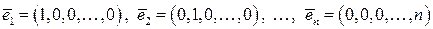Легко видеть, что она линейно независима. Теперь наряду с этой рассмотрим другую систему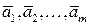 
. Ясно, что 
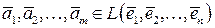, поскольку 
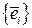являются базисом пространства 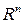. отсюда следует, что ранг системы векторов 
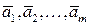не превосходит числа 
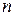. Теорема доказана.
Теорема 5. Если конечная система векторов имеет ранг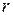 
, то любая ее подсистема, состоящая из 
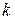векторов при 
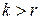- линейно зависима.
|
|
|
Доказательство. При нулевых векторах теорема очевидна. Пусть дана система векторов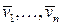 
и она имеет базис 
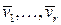. Рассмотрим некоторую подсистему данной системы векторов, состоящую из векторов 
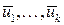, тогда векторы данной подсистемы
.
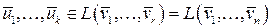Тогда мы имеем по следствию 1, что система векторов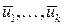 
- линейно зависима.
Теорема 6. Пусть ранг системы векторов
, 
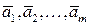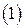
равен рангу следующей системы векторов
. 
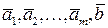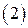
Тогда вектор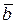 
можно представить в виде л.к. векторов системы .
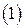Доказательство. Если ранг системы равен нулю, то теорема очевидна. пусто ранг системы векторов 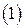равен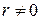 
и векторы 
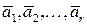- базис системы 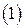. По условию теоремы ранг системы 
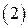также равен 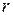, т.е. подсистема 
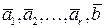линейно зависима. Тогда вектор 
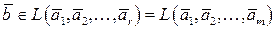. Это значит, что вектор 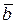- линейная комбинация системы векторов .
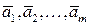Пример. Дана система векторов
.
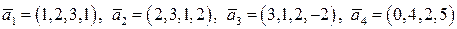Найти базис и ранг системы векторов; выразить через найденный базис все остальные векторы системы.
Решение. Составим из данных векторов матрицу и с помощью цепочки э.п. приведем ее к ступенчатому виду:
|
|
|
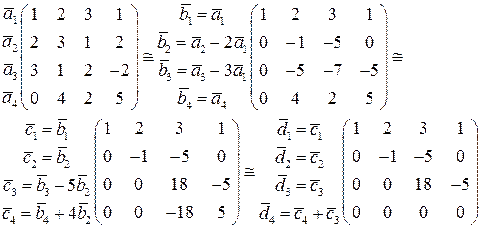
Ступенчатая матрица имеет нулевую строку. Значит система векторов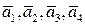 
- линейно зависима, причем векторы 
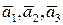образуют базис. Поэтому ранг этой системы векторов равен 3. Раз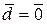 
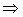
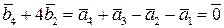
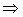
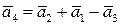, т.е. мы нашли выражение вектора 
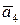через базисные векторы.
Дата добавления: 2019-03-09; просмотров: 1309; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!