Эквивалентные системы векторов
Векторные системы
Определение векторного пространства
Пусть дано поле действительных чисел 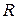 . Всякое непустое множество
. Всякое непустое множество 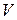 называется векторным пространством над полем
называется векторным пространством над полем 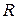 , если на этом множестве задана бинарная операция сложения и операция умножения на скаляр, причем выполняются следующие условия (аксиомы векторного пространства):
, если на этом множестве задана бинарная операция сложения и операция умножения на скаляр, причем выполняются следующие условия (аксиомы векторного пространства):
-
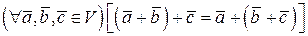 ;
; -
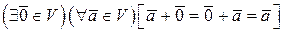 ;
; -
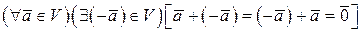 ;
; -
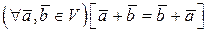 ;
; -
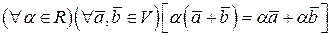 ;
; -
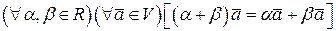 ;
; -
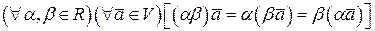 ;
; -
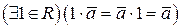 .
.
Арифметическое 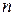 -мерное векторное пространство
-мерное векторное пространство
Пусть нам дано поле действительных чисел 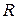 . Рассмотрим так называемое декартово произведение множеств
. Рассмотрим так называемое декартово произведение множеств
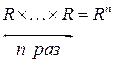
Элементом этого множества будет упорядоченная система чисел 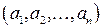 . Ее мы будем обозначать
. Ее мы будем обозначать 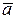 и называть
и называть 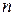 -мерным вектором.
-мерным вектором.
Рассмотрим еще один 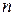 -мерный вектор
-мерный вектор 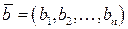 . Числа
. Числа 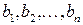 назовем координатами этого вектора и введем в рассмотрение сумму векторов
назовем координатами этого вектора и введем в рассмотрение сумму векторов 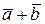 :
:
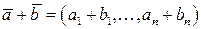 .
.
Возьмем 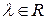 и
и 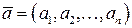 . Определим произведение скаляра
. Определим произведение скаляра 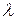 на вектор
на вектор 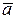 следующим образом:
следующим образом:
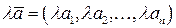 .
.
Легко видеть, что 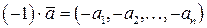 . Этот вектор мы будем называть противоположным для
. Этот вектор мы будем называть противоположным для 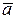 и обозначать
и обозначать 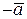 .
.
Множество всех 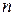 -мерных векторов обозначают через
-мерных векторов обозначают через 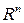 . Легко видеть, что множество
. Легко видеть, что множество 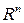 обладает структурой векторного пространства, т.е. на множестве
обладает структурой векторного пространства, т.е. на множестве 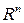 для операции сложения векторов и умножения вектора на скаляр выполняются аксиомы 1-8 векторного пространства. Поэтому множество
для операции сложения векторов и умножения вектора на скаляр выполняются аксиомы 1-8 векторного пространства. Поэтому множество 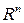 называют арифметическим
называют арифметическим 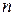 -мерным векторным пространством.
-мерным векторным пространством.
Пример. Найти линейную комбинацию 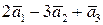 , если
, если 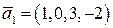 ,
, 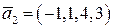 ,
, 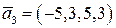 .
.
Решение: найдем векторы
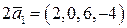 ,
, 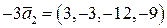 ,
, 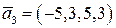 .
.
Складывая их, получим:
|
|
|
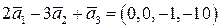 .
.
Линейная зависимость и независимость системы векторов
Пусть дана система векторов
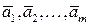
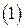
из 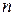 -мерного векторного пространства
-мерного векторного пространства 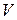 над полем
над полем 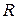 . Составим выражение
. Составим выражение
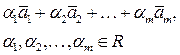
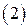
и назовем это выражение линейной комбинацией векторной системы 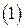 . Скаляры называют коэффициентами этой линейной комбинации. Если все коэффициенты в выражении
. Скаляры называют коэффициентами этой линейной комбинации. Если все коэффициенты в выражении  равны нулю, то линейная комбинация называется тривиальной.
равны нулю, то линейная комбинация называется тривиальной.
Составим следующее выражение:
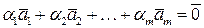 .
. 
Если равенство 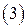 выполняется только при нулевых коэффициентах
выполняется только при нулевых коэффициентах 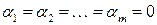 , то говорят, что система векторов
, то говорят, что система векторов 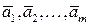 линейно независима. Если существует хотя бы один коэффициент
линейно независима. Если существует хотя бы один коэффициент 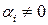 , что выполняется равенство
, что выполняется равенство 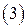 , то говорят, что система векторов
, то говорят, что система векторов 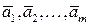 линейно зависима.
линейно зависима.
Будем говорить, что вектор 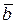 есть линейная комбинация векторов
есть линейная комбинация векторов 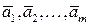 , если выполняется следующее условие:
, если выполняется следующее условие:
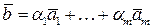 .
.
Под линейной оболочкой векторов системы 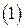 будем понимать множество всевозможных линейных комбинаций векторов этой системы. Линейную оболочку векторов системы
будем понимать множество всевозможных линейных комбинаций векторов этой системы. Линейную оболочку векторов системы 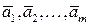 будем обозначать
будем обозначать
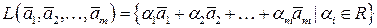 .
.
Теорема 1. система векторов, содержащая нулевой вектор линейно зависима.
|
|
|
Доказательство.Пусть нам дана система векторов 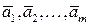 . Предположим, что она содержит нулевой вектор
. Предположим, что она содержит нулевой вектор 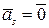 . Составим выражение:
. Составим выражение:
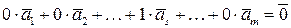 .
.
Поскольку коэффициент при векторе 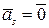 отличен от нуля, то из последнего равенства следует, что исходная система векторов линейно зависима.
отличен от нуля, то из последнего равенства следует, что исходная система векторов линейно зависима.
Теорема 2. Система векторов линейно зависима, если какая-нибудь ее подсистема линейно зависима.
Доказательство. Пусть дана система векторов 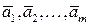 , которая содержит линейно зависимую подсистему
, которая содержит линейно зависимую подсистему 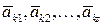 , поэтому
, поэтому
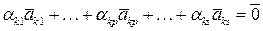 , где
, где 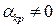 .
.
Тогда справедливо:
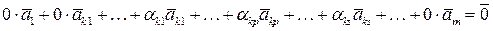 .
.
Откуда следует, что система 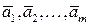 линейно зависима.
линейно зависима.
Следствие. Любая подсистема линейно независимой системы векторов линейно независима.
Теорема 3. Система векторов 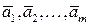 , где хотя бы один вектор (например,
, где хотя бы один вектор (например, 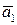 ) отличен от нуля, линейно зависима тогда и только тогда, когда какой-нибудь вектор этой системы есть линейная комбинация остальных векторов этой же системы.
) отличен от нуля, линейно зависима тогда и только тогда, когда какой-нибудь вектор этой системы есть линейная комбинация остальных векторов этой же системы.
Доказательство. Пусть дана система векторов 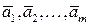 , удовлетворяющая условиям теоремы и пусть она линейно зависима. Тогда существует хотя бы один коэффициент
, удовлетворяющая условиям теоремы и пусть она линейно зависима. Тогда существует хотя бы один коэффициент 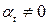 , что выполняется следующее равенство:
, что выполняется следующее равенство:
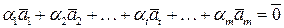 .
.
Тогда:
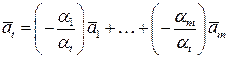 .
. 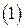
Обратно. Пусть вектор 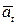 – линейная комбинация остальных векторов системы, т.е. выполняется
– линейная комбинация остальных векторов системы, т.е. выполняется 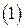 . Тогда можно записать:
. Тогда можно записать:
|
|
|
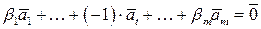
Следовательно, 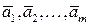 линейно зависима. Теорема доказана.
линейно зависима. Теорема доказана.
Теорема 4. Если система векторов 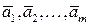 - линейно независима, а система векторов
- линейно независима, а система векторов 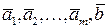 - линейно зависима, то
- линейно зависима, то 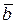 - линейная комбинация системы векторов
- линейная комбинация системы векторов 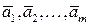 , причем единственная.
, причем единственная.
Доказательство. Предположим, что система векторов 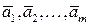 линейно независима. Тогда равенство
линейно независима. Тогда равенство 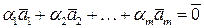 выполняется только при нулевых коэффициентах, т.е.
выполняется только при нулевых коэффициентах, т.е.
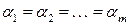 .
. 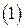
Но система векторов 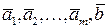 - линейно зависима. Тогда равенство
- линейно зависима. Тогда равенство
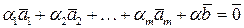
выполняется хотя бы при одном коэффициенте, отличном от нуля. Но, учитывая равенство 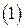 , видим, что
, видим, что 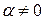 . Из последнего равенства мы можем найти вектор
. Из последнего равенства мы можем найти вектор 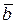 как линейную комбинацию векторов:
как линейную комбинацию векторов:
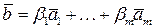 .
. 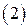
Равенство 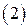 единственно. Докажем это методом от противного.
единственно. Докажем это методом от противного.
Пусть имеет место другое разложение 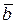 по векторам
по векторам 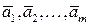 , т.е.:
, т.е.:
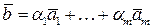 .
. 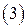
Вычитая из равенства 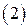 равенство
равенство 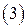 почленно, получим:
почленно, получим:
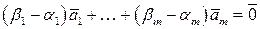 .
.
Но 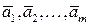 линейно независимы. Поэтому последнее равенство справедливо только при нулевых коэффициентах:
линейно независимы. Поэтому последнее равенство справедливо только при нулевых коэффициентах:
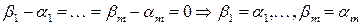 .
.
Теорема 5. Если 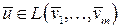 , а
, а 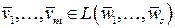 , то
, то 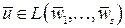 .
.
Доказательство. Т.к. 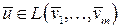 , то
, то
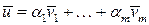 .
. 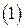
|
|
|
Т.к. 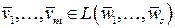 , то
, то
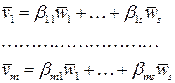
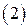
Подставляя в равенство 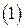 вместо векторов
вместо векторов 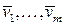 их значения по формулам
их значения по формулам 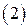 , получим, что
, получим, что  - линейная комбинация векторов
- линейная комбинация векторов 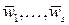 , т.е.
, т.е. 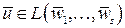 . Теорема доказана.
. Теорема доказана.
Теорема 6. Если система векторов 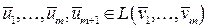 , то векторы
, то векторы 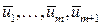 линейно зависимы.
линейно зависимы.
Доказательство. Пусть
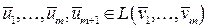 .
. 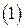
Предположим, что это система ненулевых векторов. Докажем теорему методом математической индукции по числу 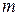 . Проверим справедливость теоремы при
. Проверим справедливость теоремы при 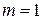 . Поскольку имеет место условие
. Поскольку имеет место условие 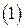 , то
, то
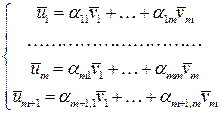
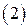
1) Пусть 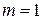 . Из
. Из 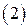 следует:
следует:
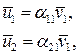
т.е. векторы 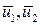 линейно зависимы. При
линейно зависимы. При 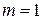 теорема верна.
теорема верна.
2) Предположим, что теорема верна при 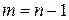 и на этом основании докажем, что она верна и при
и на этом основании докажем, что она верна и при 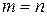 . Пусть
. Пусть 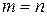 , тогда система
, тогда система 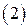 примет следующий вид:
примет следующий вид:
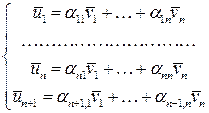
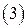
Если в правых частях системы 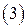 все коэффициенты при векторе
все коэффициенты при векторе 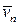 равны нулю, то получим, что
равны нулю, то получим, что 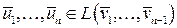 . Значит по индуктивному предположению система векторов
. Значит по индуктивному предположению система векторов 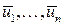 - линейно зависима, а, значит, будет линейно зависимой и система векторов
- линейно зависима, а, значит, будет линейно зависимой и система векторов 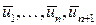 . если хотя бы один из коэффициентов при векторе
. если хотя бы один из коэффициентов при векторе 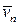 отличен от нуля, например,
отличен от нуля, например, 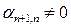 , то, исключая вектор
, то, исключая вектор 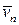 из первых
из первых 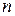 равенств, получим:
равенств, получим:
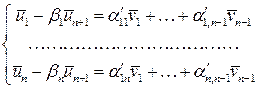
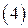
Из 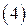 следует, что система векторов
следует, что система векторов 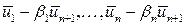 линейно зависима, откуда
линейно зависима, откуда
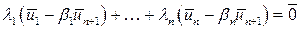 ,
,
где хотя бы один из коэффициентов отличен от нуля. Откуда следует, что система векторов 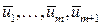 линейно зависима. теорема доказана.
линейно зависима. теорема доказана.
Следствие 1. Если система векторов 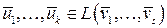 , где
, где 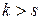 , то система векторов линейно зависима.
, то система векторов линейно зависима.
Следствие 2. Если система векторов 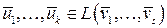 и система векторов
и система векторов 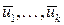 линейно независима, то
линейно независима, то 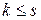 .
.
Эквивалентные системы векторов
Пусть даны две системы векторов: 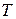 и
и 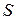 . Будем говорить, что две системы векторов
. Будем говорить, что две системы векторов 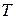 и
и 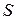 находятся в отношении
находятся в отношении 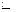 , если каждый ненулевой вектор одной из этих систем можно представить в виде линейной комбинации векторов другой системы. Записывается следующим образом:
, если каждый ненулевой вектор одной из этих систем можно представить в виде линейной комбинации векторов другой системы. Записывается следующим образом:
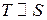
Легко видеть, что данное отношение есть отношение эквивалентности, т.е. оно рефлексивно, симметрично и транзитивно.
Из определения эквивалентности двух систем векторов непосредственно следует:
1) 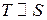
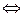 их линейные оболочки равны;
их линейные оболочки равны;
2) если две конечные системы векторов эквивалентны и каждая из них линейно независима, то эти системы состоят из одинакового числа векторов.
Под элементарными преобразованиями (э.п.) конечной системы векторов будем понимать:
1) умножение какого-нибудь вектора системы на скаляр 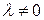 ;
;
2) прибавление (вычитание) к одному из векторов системы другого вектора данной системы, умноженного на скаляр;
3) исключение из системы или введение в систему нулевого вектора, причем это преобразование называется особенным.
Теорема 1. Если одна из конечных систем векторов получается из другой системы векторов в результате цепочки э.п., то эти системы векторов эквивалентны.
Доказательство. Пусть дана конечная система векторов
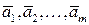 .
. 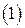
Перейдем от этой системы к следующей системе:
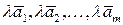 ,
, 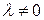 .
. 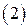
Ясно, что 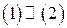 .
.
Перейдем от системы 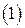 к следующей системе:
к следующей системе:
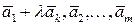 ,
, 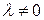 .
. 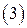
Легко видеть, что 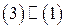 . Применяя к
. Применяя к 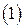 э.п. вида 1) и 2), снова приходим к эквивалентной системе.
э.п. вида 1) и 2), снова приходим к эквивалентной системе.
Следует заметить, что применение к системе 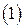 преобразование вида 3), снова приведет к эквивалентной системе. Поэтому в силу транзитивности отношения
преобразование вида 3), снова приведет к эквивалентной системе. Поэтому в силу транзитивности отношения 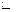 система векторов, получающаяся из системы
система векторов, получающаяся из системы 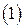 в результате цепочки э.п. снова эквивалентна исходной системе.
в результате цепочки э.п. снова эквивалентна исходной системе.
Дата добавления: 2019-03-09; просмотров: 1506; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
