Когда человек теряет богатство, он ничего не теряет. Когда человек теряет здоровье, он теряет кое-что. Когда человек теряет характер, он теряет все. © Билли Грэм 1003 - | 775 - или читать все...
Обратная связь Пожаловаться на материал

Расчет переходной и импульсной характеристик цепи


⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Чтобы судить о возможностях электротехнических устройств, принимающих и передающих входные воздействия, прибегают к исследованию их переходных и импульсных характеристик.

Переходная характеристика h(t) линейной цепи, не содержащей независимых источников, численно равна реакции цепи на воздействие единичного скачка тока или напряжения в виде единичной ступенчатой функции 1(t) или 1(t – t0) при нулевых начальных условиях (рис. 14). Размерность переходной характеристики равна отношению размерности реакции к размерности воздействия. Она может быть безразмерной, иметь размерность Ом, Сименс (См).

 

 

Импульсная характеристика k(t) линейной цепи, не содержащей независимых источников, численно равна реакции цепи на воздействие единичного импульса в виде d(t) или d(t – t0) функции при нулевых начальных условиях. Ее размерность равна отношению размерности реакции к произведению размерности воздействия на время, поэтому она может иметь размерности с–1, Ом×с–1, См×с–1.

Импульсную функцию d(t) можно рассматривать как производную единичной ступенчатой функции d(t) = d1(t)/dt. Соответственно, импульсная характеристика всегда является производной по времени от переходной характеристики: k(t) = h(0+)d(t) + dh(t)/dt. Эту связь используют для определения импульсной характеристики. Например, если для некоторой цепи h(t) = 0,7e–100t, то k(t) = 0,7d(t) – 70e–100t. Переходную характеристику можно определить классическим или операторным методом расчета переходных процессов.

Между временными и частотными характеристиками цепи существует связь. Зная операторную передаточную функцию, можно найти изображение реакции цепи: Y(s) = W(s)×X(s), т.е. передаточная функция содержит полную информацию о свойствах цепи как системы передачи сигналов от ее входа к выходу при нулевых начальных условиях. При этом характер воздействия и реакции соответствуют тем, для которых определена передаточная функция.

Передаточная функция для линейных цепей не зависит от вида входного воздействия, поэтому она может быть получена из переходной характеристики. Так, при действии на входе единичной ступенчатой функции 1(t) передаточная функция с учетом того, что 1(t) = 1/s, равна

W(s) = L[h(t)] / L[1(t)] = L[h(t)] / (1/s), где L[f(t)] — обозначение прямого преобразования Лапласа над функцией f (t). Переходная характеристика может быть определена через передаточную функцию с помощью обратного преобразования Лапласа, т.е. h(t) = L–1[W(s)(1/s)], где L–1[F(s)] — обозначение обратного преобразования Лапласа над функцией F(s). Таким образом, переходная характеристика h(t) представляет собой функцию, изображение которой равно W(s) /s.

При действии на вход цепи единичной импульсной функции d(t) передаточная функция W(s) = L[k(t)] / L[d(t)] = L[k(t)] / 1 = L[k(t)]. Таким образом, импульсная характеристика цепи k(t) является оригиналом передаточной функции. По известной операторной функции цепи с помощью обратного преобразования Лапласа можно определить импульсную характеристику: k(t)  W(s). Это означает, что импульсная характеристика цепи единственным образом определяет частотные характеристики цепи и наоборот, так как

W( jw) = W(s)s = jw. Поскольку по известной импульсной характеристике можно найти переходную характеристику цепи (и наоборот), то последняя тоже однозначно определяется частотными характеристиками цепи.

Пример 8. Рассчитать переходную и импульсную характеристики цепи (рис. 15) для входного тока и выходного напряжения при заданных параметрах элементов: R = 50 Ом, L1 = L2 = L = 125 мГн,
С = 80 мкФ.

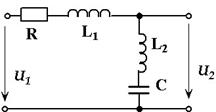
Решение. Примéним классический метод расчета. Характеристическое уравнение Zвх = R + pL +
+ 1 / (pC) = 0 при заданных параметрах элементов имеет комплексно-сопряженные корни: p1,2 =
= – d ±  jwсв = – 100 ±  j200, что определяет колебательный характер переходного процесса. В этом случае законы изменения токов и напряжений и их производных в общем виде записывают так:

y(t) = (M сoswсвt + N sinwсвt)e–dt + yвын; dy(t) / dt =

=[(–Md  + Nwсв) ´ сos wсвt – (Mwсв + Nd)sinwсвt]e–dt + dyвын / dt, где wсв — частота свободных колебаний; yвын — вынужденная составляющая переходного процесса.

Вначале найдем решение для uC (t) и iC (t) = C duC (t) / dt, воспользовавшись вышеприведенными уравнениями, а затем по уравнениям Кирхгофа определим необходимые напряжения, токи и, соответственно, переходные и импульсные характеристики.

Для определения постоянных интегрирования необходимы начальные и вынужденные значения указанных функций. Их начальные значения известны: uC (0+) = 0 (из определения h(t) и k(t)), так как i C (t) = i L(t) = i(t), то i C (0+) = i L(0+) = 0. Вынужденные значения определим из уравнения, составленного согласно второму закону Кирхгофа для t  0+: u1 = R i(t) + (L1 + L2) i(t) / dt + u C(t), u1 = 1(t) = 1 = сonst,

отсюда u C(¥) = uC вын = 1, i C (¥) = i C вын = i(¥) = 0.

Составим уравнения для определения постоянных интегрирования M, N:

u C (0+) = M + uC вын (0+), iC (0+) = С(–Md  + Nwсв) + i C вын (0+); или: 0 = M + 1; 0 = –M 100  +  N 200; отсюда: M = –1, N = –0,5. Полученные значения позволяют записать решения uC(t) и iC (t) = i(t): u C (t) = [–сos200t – -0,5sin200t)e–100t + 1] B, i C (t) = i(t) = [80×10–6(100 - 100)сos200t – (–200 - 50) sin200t)]e–100t] = 0,02 ´
´ sin200t)e–100t A. Согласно второму закону Кирхгофа,

u2 (t) = uC (t) + u L2 (t), u L2 (t) = u L (t) = Ld i(t) / dt = (0,5сos200t – 0,25sin200t) ´ e–100t B. Тогда u2 (t) =

 =(–0,5сos200t – 0,75sin200t) e–100t + 1 = [–0,901sin(200t + 33,69°) e–100t + 1] B.

Проверим правильность полученного результата по начальному значению: с одной стороны, u2 (0+) = –0,901 sin (33,69°) + 1 = 0,5, а с другой стороны, u2 (0+) = uС (0+) + u L (0+) = 0 + 0,5 — значения совпадают.

Определим переходные и импульсные характеристики схемы: hi (t) = i(t) / u1(t) = i(t) / (1 B) = 0,02 sin200t e–100t См; ki (t) = hi(0+) d(t) + dhi (t) / dt = (4 сos200t – 2 sin200t) e–100t См/с; hu2 (t) =
= u2(t) / u1(t) = u2 (t) / (1 B) = [–0,901sin(200t + 33,69°) e–100t + 1] б/р, ku2 (t) = hu2 (0+) d(t) + dhu2 (t) / dt = 0,5d(t) + (–180,2 сos200t + 90,1 sin200t) e–100t с–1.

Расчет переходных процессов

Пример 9. Рассчитать изменение тока i1 и напряжения u2 в схеме четырехполюсника (рис. 16, а) для режима холостого хода (Zн = ¥) на интервале t0 £ t £ t0 + T при подключении его к клеммам с напряжением u12 в момент t0, когда напряжение u11(t0) = 0, du11(t0)/dt > 0, т.е. в момент перехода отрицательной полуволны напряжения в положительную (рис. 16, б). Значения параметров элементов схемы и входного напряжения: R1 = 45 Ом, R2 = 8 Ом,
R3 = 10 Ом, L = 50 мГн, С = 250 мкФ, u11(t) = 14,1sin(103t + p/4) B, u12(t) = [20, t0+ £ t £ t0 + T/2– ; –20, t0 + T/2+ £ t £ t0+ T–], T = 6,28 × 10–3 с.

Рис. 16

Решение. Подготовим схему — выберем условно положительные направления токов и напряжений. Определим независимые начальные условия uC (t0+) и iL(t0+) из значений uC (t) и iL(t), рассчитанных до коммутации: uC (t0+) = uC (t0–), iL(t0+) = iL(t0–). Значение uC (t) и iL(t) = i1(t) рассчитаем с использованием метода комплексных амплитуд: I1m = U1m / Zвх, U1m = 14,1e jp/4,   Zвх = R1 + jwL1 + R3 + R2(–j / wC) / (R2 – j / wC) = =45 + j50 + 10 + 8(–j4) / (8 – j4) = 56,6 + j46,8. Тогда I1m = (10 + j10)/(56,6 + j46,8) = (0,1917 + j0,0182) = =0,193exp( j5,42°)  i1(t) = 0,193sin(103t + 5,42°). Напряжение UCm = Zbc I1m = [R2(–j / wC) / (R2 – j / wC)] I1m = =(1,6 – j3,2) ´ (0,1917 + j0,0182) = 0,365 – j0,584 = 0,689exp(–j58°)

 uC (t) = 0,689sin(103t – 58°).

Определим время коммутации t0 из заданного условия u11(t0) = 0, du11(t0) / dt > 0: u11(t0) = 14,1sin(wt0 + p/4) = 0, отсюда t0 = –p/(4w), wt0 = –p/4 = – 45°. Соответственно, iL(t0–) = iL(t0+) = 0,193sin(– 45° + 5,42°) =

= – 0,123; uC (t0+) = uC (t0–) = 0,689sin(– 45° – 58°) = – 0,671.

В последующем расчете начало отсчета t0 примем за ноль, тогда iL(t0+) = iL(0+) = – 0,123 А, uC (t0+) =

= uC (0+) = – 0,671 В.

Характер переходного процесса зависит от корней характеристического уравнения. Характеристическое уравнение составим методом входного сопротивления: Z( p) = R1 + pL + R3 + (R2 / pC ) /
/ (R2 + 1 / pC) = 0. После преобразования получим Z( p) = p2 +
+ p[(R1R2C + L) / (R2LC )] + (R1 + R2) / ( R2LC ) = 0. Введем обозначения и рассчитаем

d  = (R1R2C + L) / (2R2LC ) = 800,  = (R1 + R2) /  (R2LC) = 630 000:  p2 + 2dp +  =  p2 + 2800p + 630 000 = 0, корни p1,2 = – d ± 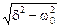= – 800 ± = – 800 ±100, p1 = – 700 с–1, p2 = – 900 с–1.

На основании полученных корней запишем выражения для токов, напряжений и их производных (так как система второго порядка) в общем виде:

                          y(t) = yсв + yвын=A1exp( p1t) + A2exp( p2t) + yвын;

                         dy(t)/dt = p1A1exp( p1t) + p2A2exp( p2t) + dyвын/dt.                     (1)

Для определения зависимых начальных условий и установившихся значений токов и напряжений составим систему уравнений согласно законам Кирхгофа, которая будет справедлива на интервале

0+ £ t £ ¥:

                      u12(t) = R1i1 + uL + R3i1 + uC, uC – R2i2 = 0, i1 = i2 + i3.                 (2)

Первый интервал 0+ £ t £ T/2– : u12(t) = 20 В.

Найдем зависимые начальные условия для момента коммутации ключа t0+, для которого

iL(0+) = i1(0+) = – 0,123 А, uC (0+) = – 0,671 В: i2(0+) = – 0,0839 А, i3(0+) = – 0,207 А, uL (0+) = 27,436 В.

Определим вынужденные значения (t = ¥) токов и напряжений из уравнений (2), зная, что при постоянном (не изменяющемся во времени) воздействии uL(¥) = 0, i3(¥) = i С (¥) = 0. Получим:

i1(¥) = u12 / (R1 + R2 + R3) = 0,317 А, uC (¥) = i1(¥)R2 = 2,54 В.

Составим уравнения для определения постоянных интегрирования выражений i1(t) и uL(t) согласно (1): i1(0+) = A1 + A2 + i1(¥), uL(0+) = L(di1/dt)(0+) = L(p1A1 +p2A2) + uL(¥); –0,123 = A1 + A2 +
+ 0,317; 27,436 = 0,05[(–700) A1 + (– 900) A2] + 0. Решая уравнения, найдем A1 = 0,761, A2 = – 1,202. Окончательно решение для i1(t) и uL(t): i1(t) = (0,761e–700t – 1,202e–900t + 0,317) А, uL(t) = (–26,635e–700t +
+ 54,1202e–900t) В.

Аналогично, используя начальные и вынужденные значения, найдем решение для u С (t) и i3(t) = i С (t) = С du С / dt на первом интервале входного воздействия:

u С (t) = (– 15,24e–700t + 12,02e–900t + 2,54) В; i3(t) =

=(2,665e–700t – 2,704e–900t) А; u2(t) = u С(t) + i1(t)R3 = (– 7,63e–700t + 5,715) В.

Второй интервал T/2+ £ t £ T– : u12(t) = – 20 В.

Скачкообразное изменение входного напряжения в момент
t = T/2 создало новые условия для протекания переходного процесса. Методика расчета аналогична методике для первого интервала. Прежними остаются только корни, так как структура и параметры элементов схемы не изменились, а напряжение источника входного воздействия на корни не влияет.

Независимые начальные условия uC (T/2+) и iL(T/2+) = i1(T/2+) определим из uC (t) и iL(t) первого интервала: uC (T/2+) = uC (T/2–) = (–15,24e–700T/2 + 12,02e–900T/2 + 2,54) = 1,56, i1(T/2+) = i1(T/2–) =
= (0,761e–700T/2 – 1,202e–900T/2 + 0,317) = 0,331, T/2 = 3,14 × 10–3 с.

Зависимые начальные условия и вынужденные значения токов и напряжений вычислим, воспользовавшись уравнениями (2): i2(T/2+) = 0,195 А, i3(T/2+) = 0,136 А, uL(T/2+) = – 39,765 В; uL(¥) = 0 В, i3(¥) = 0 А, i1(¥) = i2(¥) = u12 / (R1 + R2 + R3) = – 0,317 А, uC(¥) = R2i2(¥) = – 2,54 В.

Решение для i1(t) и u2(t) найдем, используя uC (t) и iC (t) и уравнения (2). С учетом смещения процессов по оси времени относительно начала отсчета получим: uC (t) = uCсв + uCвын = A1 ´
´ exp[p1(t – T/2)] + A2 exp[p2(t – T/2)] + uCвын; iC(t) = CduC (t) / dt =
= Cp1A1exp[(p1(t – T/2)] + Cp2A2exp[(p2t – T/2)]+ iCвын.

При t = (T/2+): uC (T/2+) = A1 + A2 + uCвын(T/2+); iC (T/2+) = Cp1A1 + Cp2A2 + iCвын(T/2+). Подставляя в эту систему начальные и вынужденные значения токов и напряжений, найдем постоянные интегрирования: – 1,56 = A1 + A2 – 2,54; 0,136 = 0,05(– 700)A1 + 0,05 ´ (– 900) A2; A1 = 21,17; A2 = –17,07. Следовательно,

uC (t) = {21,17exp[–700(t – T/2)] – 17,07exp[–900(t – T/2)] – 2,54} B;
iC(t) = i3(t) = {–3,705exp[(–700(t – T/2)] + 3,841exp[(–900(t – T/2)]} A;

 i2(t) = u С (t)/R2 = {2,646exp[–700(t – T/2)] – 2,134exp[–900(t – T/2)] –
– 2,54} A; i1(t) = i2(t) + i3(t) = {– 1,06 exp[–700(t – T/2)] + 1,71 ´ exp[– 900(t – T/2)] – 0,317} A;

 u2(t) = u С(t) + i1(t)R3 = {10,58 ´ exp[– 700(t – T/2)] – 5,715} B.

Чтобы убедиться в правильности полученных результатов, выполним проверку:

1. Определим из найденных решений значения i1(T/2–) и i1(T/2+). Согласно закону коммутации, i1(t) = iL(t) не может измениться скачком, т.е. i1(T/2–) = i1(T/2+): i1(T/2–) = 0,331 А, i1(T/2+) =
= 0,3305 А — равенство соблюдается с достаточной точностью.

2. Изменение входного напряжения u12(t) в момент t = T/2 на (–2U12) = – 40 B может уравновесить в данной схеме только напряжение на индуктивность, так как остальные напряжения скачком измениться не могут, следовательно, uL(T/2+) – uL(T/2–) = – 40. Проверим, используя найденные решения:

uL(T/2+) = u12(T/2+) – uС(T/2+) – i1(T/2+)(R1 + R3) = – 39,765 В, uL(T/2–) = 0,248 В, uL(T/2+) – uL(T/2–) =

= –39,765 – 0,248 = –40,013 В — результаты совпадают с достаточной точностью. При первой коммутации изменение напряжения на индуктивном элементе UL должно равняться 20 В (проверьте!).

Расчет электрической цепи частотным методом
при несинусоидальном воздействии

Расчет линейной электрической цепи при периодическом несинусоидальном воздействии на основании принципа суперпозиции проводится для каждой составляющей воздействия (после разложения его в ряд Фурье) отдельно, так, как если бы в цепи действовала только эта составляющая. Расчет цепи для постоянной составляющей проводится так же, как в случае, когда к цепи подключен источник постоянного напряжения.

При расчете цепи для отдельных гармонических составляющих следует пользоваться символическим методом (методом комплексных амплитуд). Для k-й гармоники комплексное сопротивление ветви, содержащей последовательно соединенные элементы R, L и C, Z(k ) = R + jkw1L – j/(kw1C), где w1 = 2p / T = 2p f  — частота основной (первой) гармоники, k — номер гармоники (k = 1, 2, 3, ...).

Выбранный метод расчета цепи (по законам Кирхгофа, контурных токов и т.д.) для одной гармонической составляющей не зависит от метода расчета той же цепи для другой гармоники. Из выражения для комплексной передаточной функции W( jw) = Y( jw) / X( jw) = Ym( jw) / Xm( jw), определяемой как отношение комплексных амплитуд (комплексных действующих значений) электрических величин на выходе и входе цепи в заданном режиме работы, следует, что при заданном гармоническом воздействии
uвх = Umвхsin(wt +yu) выходное напряжение можно определить следующим образом:

U mвых = W( jw)U mвх = W(w )Umвхexp[ j(yuвх + j)].

Так как периодическое несинусоидальное воздействие имеет дискретный спектр с частотами kw1, то при действии на вход цепи k-й гармоники появится реакция с частотой kw1, амплитудой

Umвых = W(kw1)Umвх и начальной фазой yuвых = [yuвх + j(kw1)].  Здесь W(kw1) — модуль, j(kw1) — аргумент коэффициента передачи по напряжению цепи на частоте kw1.

Суммируя все выражения для мгновенных значений гармоник, включая постоянную составляющую выходного напряжения, согласно принципу суперпозиции будем иметь выражение для выходного напряжения.

Пример 11. Для схемы четырехполюсника (см. рис. 2) рассчитать uвых(t) при входном воздействии u1(t) в виде разнополярных прямоугольных импульсов (рис. 17), ряд Фурье которого содержит только синусоидальные составляющие нечетных гармоник (k = 1, 3, 5, ...): u1(t) = = .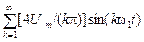

 

Решение. Будем считать АЧХ и ФЧХ заданного четырехполюсника
известными (см. пример 5): W(w) = 1 / / [(1 – w2LC)2 + (wRC)2]1/2, j(w) = -jarctg[wRC/(1 – w2LC)].

На рис. 13 показаны графики этих характеристик.

Заменим в АЧХ и ФЧХ текущую частоту w на дискретную kw1:

W(kw1) = 1/[(1 – k2w12LC)2 + (kw1RC)2]1/2, j(kw1) = - jarctg[kw1RC/(1 – k2w12LC)].  

Выходное напряжение в общем виде может быть записано следующим образом:

Нетрудно заметить, что четырехполюсник осуществляет изменение спектра входного напряжения. Вследствие этого выходное напряжение отличается по форме от входного воздействия.

 

Дата добавления: 2019-03-09; просмотров: 2568; Мы поможем в написании вашей работы!

Поделиться с друзьями:


⇐ Предыдущая123Следующая ⇒


Мы поможем в написании ваших работ!
.
.
© 2014-2024 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.042)