Спектральное представление сигналов
Основы теории сигналов
Электрические сигналы
Виды сигналов
Сигнал – это любой материальный носитель информации, являющийся функцией во времени.
| Рисунок 1.1 - Пример сигнала |
Зависимость функции сигнала от времени S( t) – может иметь различную размерность: световой поток, звуковое давление и пр. В теории сигналов обычно s(t) – обобщённое название амплитуды, так сказать «сигнал вообще», независимо от его размерности (рисунок 1.1). В электронике сигналом почти всегда является функция напряжения u( t), значительно реже – тока i( t). В дальнейшем по умолчанию будем обозначать сигнал в виде напряжения: u( t).
Сигналы можно разделить на детерминированные и случайные. Значение детерминированного сигнала точно определено в любой момент времени, а случайного – нет.
Теоретически любой сигнал является случайным, со своим средним значением, дисперсией и др. Однако, для упрощения описания и изучения сигналов используется их идеализированная математическая модель, и считают сигнал детерминированным.
Сигналы можно разделить на непрерывные, дискрет-ные и дискретно-непрерывные.
В непрерывных сигналах (называемых также аналоговы-ми) и значение сигнала u( t) и время t могут принимать бесконечное множество значений (в определенном диапазоне). Пример аналогового сигнала показан на рисунке 1.2.
| Рисунок 1.2 - Пример графика аналогового сигнала |
| Рисунок 1.3 - Пример дискретного сигнала |
|
|
|
В дискретно-непрерывных сигналах один параметр является дискретным, а другой непрерывным. Например, на рисунке 1.4а u( t) - является дискретным параметром, а время t – непрерывным, а на рисунке 1.4б – наоборот.
Реальные сигналы, очевидно, являются непрерывными, но, если время переходного процесса достаточно мало, для упрощения считаются дискретными
| Рисунок 1.4 – Дискретно-непрерывные сигналы |
| Рис. 4. Пример дискретно-непрерывного сигнала |
| Рисунок 1. 5 - Последовательность прямоугольных импульсов |
Такие импульсы имеют два уровня: логический ноль «0» (при этом U( t)< U °) и логическая единица «1» (U( t)> U ¢); и называются цифровыми.
Основными характеристиками цифровых прямоугольных импульсов являются: период Т, частота повторения импульсов f и длительность импульсов τ (читается – «тау»).
|
|
|
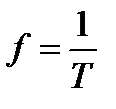- частота повторения импульсов;
- скважность;
Скважность показывает во сколько раз период повторе-ния импульсов больше их длительности. Часто используется показатель, обратный скважности, называемый по-английски: Duty Cycle (рабочий цикл), обычно измеряется в процентах.
Последовательность прямоугольных импульсов с Q = 2 (Duty Cycle 50%) называется меандром (рисунок 1.6).
| Рисунок 1.6 - Меандр (Т = 2 τ) |
Теоретически любой реальный сигнал является непре-рывным, а дискретные сигналы являются идеализированной математической моделью. Кроме того, любой реальный сигнал должен быть дифференцируемым в любой точке, т. к. теорети-чески напряжение или ток не могут измениться мгновенно.
Рассмотрим теперь реальный прямоугольный импульс. Как видно на рисунке 1.7, он является непрерывным: переход между уровнями не происходит мгновенно.
Длительность импульса t обычно определяется по уров-ню 0,1 от амплитуды U. Нарастание и спад напряжения имеют экспоненциальный характер. Участок нарастания напряжения называется фронтом (или передним фронтом), а участок спада – срезом (или задним фронтом). Для простоты их определяют между уровнями 0,1 U и 0,9 U.
t1 – длительность фронта;
t2 – длительность среза.
|
|
|
В общем случае t1 ¹ t2.
Рисунок 1.7 - Реальный прямоугольный импульс
Для любого сигнала конечной длительности t энергия сигнала равна:
.
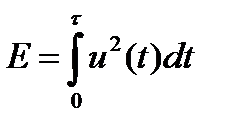Мощность сигнала равна: . 
Спектральное представление сигналов
Во многих случаях сигналы имеют сложную форму. С целью упрощения анализа и преобразования сигналов их представляют в виде конечной или бесконечной суммы элементарных (базисных) функций. (Аналог – разложение вектора в координатном базисе).
- обобщенный ряд Фурье где:
С k – постоянные коэффициенты ряда Фурье;
- базисные функции.
Таким образом, сигнал представляется в виде линейной комбинации базисных функций.
Базисные функции удобно выбирать так, чтобы они:
- имели простое аналитическое выражение;
- позволяли легко вычислять коэффициенты С k;
- достаточно просто технически реализовывались.
В качестве базисных функций в теории сигналов иногда выбирают d-функцию («дельта-функцию» или функцию Дира-ка), иногда функции Уолша и т. д.
Однако в подавляющем большинстве случаев используют разложение сигнала в ряд Фурье, т. е. в качестве базисных выбирают гармонические функции.
Пусть имеется периодический сигнал с периодом Т. Тогда его можно представить рядом Фурье:
|
|
|
Коэффициенты 
, 
, 
определяются следующим образом:
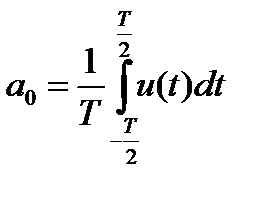- постоянная составляющая;
;
;
где 
- угловая частота
Существуют и другие формы записи ряда Фурье.
;
; 
.
Если использовать формулы Эйлера, то можно записать ряд Фурье в комплексной форме:
;
;
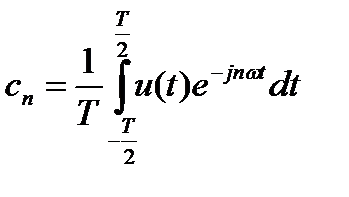В этом случае базисные функции - 
.
График зависимости амплитуды каждой гармоники от частоты w называется спектральной диаграммой. Зависимость Un( w) называется амплитудным спектром. Зависимость j n( w) называется фазовым спектром.
Как правило, более важным для анализа сигнала является амплитудный спектр. Рассмотрим его на примере одного из самых распространенных сигналов: последовательности прямоу-гольных импульсов (рисунок 1.8).
| Рисунок 1.8 - Последовательность прямоугольных импульсов сигнала |
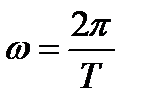, определяю-щейся периодом повторения импульсов. Таким образом, рассто-яние между соседними гармониками определяется периодом сигнала. Огибающая спектра, показанная на рисунке штрихо-вой линией, зависит от типа сигнала. То есть – для треугольных или пилообразных импульсов форма её будет другой.
Амплитуды Un спектральных составляющих с увеличени-ем их номера убывают согласно закону вида sin x)/ x:
| Рисунок 1.9 - Амплитудный спектр последовательности прямоугольных импульсов |
.
Частоты, на которых амплитуда каждой гармоники Un( w) обращается в ноль, зависят от длительности импульса. Мини-мальная из этих частот определяет эффективную ширину спек-тра Dw. Чем меньше длительность импульса, тем более широким получается спектр 
.
Аналогично может быть построен спектр фаз (фазо-частотная спектрограмма); в этом случае длины вертикальных отрезков пропорциональны начальным фазам спектральных составляющих сигнала. Так как ухо человека не реагирует на фазы колебаний, в звуковом радиовещании пользуются только амплитудно-частотными спектрограммами. В том случае, когда спектры сигналов занимают много октав, при построении спектрограмм обычно пользуются логарифмической шкалой частот, на которые откладываются не частоты, а их десятичные логарифмы.
Некоторые свойства спектров
1. При увеличении периода T частота уменьшается, линии на спектральной диаграмме сближаются, а амплитуда гармонических составляющих уменьшается.
В случае непериодического сигнала считаем, что T ® ¥, тогда спектр из линейчатого становится сплошным.
Введем понятие спектральной плотности S( w):
| Рисунок 1.10 - Спектральная плотность последовательности прямоугольных импульсов |
S( w) показывает амплитуду гармонических составляю-щих внутри полосы частот d w (заштрихованная область).
По известной S( w) одиночного импульса легко построить спектр последовательности импульсов:
.
Таким образом, форма графика спектральной плотности характеризует огибающую сигнала и зависит от формы сигнала.
2. При увеличении длительности импульса t его спектр сужается и наоборот.
Если сигналу u( t) соответствует спектральная плотность S(ω), то сигналу ku( t) соответствует спектральная плотность S( ω)/ k
Интерес представляет d-функция. Это теоретически импульс с длительностью равной нулю и бесконечно большой амплитудой. При этом интеграл от него конечен и равен едини-це, т.е. энергия сигнала конечна. d-функция имеет бесконечный равномерный спектр, называемый «белым шумом». Т.е. все амплитуды гармоник в спектре одинаковы (рисунок 1.11).
| Рисунок 1. 11 - Спектр d-функции |
Дата добавления: 2019-03-09; просмотров: 502; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!