РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ КРАМЕРА
Рассмотрим систему n линейных уравнений с n неизвестными x1,x2,…,xn:
(10)
, 
. (11)
Определителем системы (10) называется определитель матрицы из коэффициентов уравнений этой системы. Обозначим его буквой ∆. Определитель, полученный из определителя системы заменой столбца из коэффициентов при неизвестной xk свободными членами, обозначим через ∆k, где k-одно из чисел 1,2,…,n (способы вычисления ∆ рассматриваются в методических указаниях «Матрицы и определители»)
Теорема 2. Если определитель системы (10) отличен от нуля, то система имеет единственное решение
, 
, …, 
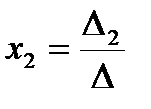, (12)
где ∆ и ∆k определены формулами (11).
Замечание. Линейная система, определитель которой отличен от нуля, называется невырожденной. Таким образом, невырожденная система имеет единственное решение, определяемое формулами Крамера.
Решить системы методом Крамера.
Пример 1
Составим определитель ∆ данной системы и определители ∆k (k=1,2):
, 
, 
.
Так как ∆=5,∆1=20,∆2=-25, то по формулам (10) получаем
, 
.
Пример 2
Составим определитель системы и определители ∆k (k=1,2,3):
, 
,
, 
.
Определитель системы ∆=-6≠0, т.е. выполнено условие теоремы 1. Вычисляем определители ∆1, ∆2, ∆3, получаем ∆1=-18,
∆2=-12,∆3=-6. Система имеет единственное решение:
|
|
|
, 
, 
.
Далее рассмотрим примеры на определение совместимости системы линейных уравнений.
Пример 3
Запишем основную матрицу A и расширенную матрицу 
данной системы:
, 
.
Очевидно, rang А=2 и rang =2. Так как rang А= rang , то система совместна.
Пример 4
В данном примере
, 
.
Поскольку det A =0, то rang A =1. В матрице имеются миноры второго порядка, отличные от нуля, поэтому rang =2. Так как rang А≠ rang , то система не совместна.
Пример 5
Запишем основную матрицу А и расширенную матрицу данной системы:
, 
.
Поскольку det A≠0, т.е.
,
то rang А=3. Очевидно, rang =3. Система совместна.
Единственность решения систем линейных уравнений
Совместная система может иметь единственное решение (в этом случае ее называют определенной) или более одного решения (тогда она называется неопределенной). Нас интересует вопрос о том, при каком условии линейная система имеет единственное решение. Ответ на этот вопрос дает следующая теорема.
Теорема 3. Если ранг матрицы совместной линейной системы равен числу неизвестных, то система имеет единственное решение.
Пример 1
Составим матрицу А и расширенную матрицу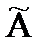 
этой системы трёх уравнений (m=3) с двумя неизвестными (n=2). Преобразуем матрицу 
:
|
|
|
, 
, 
Поскольку r= 
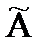=2, где – ранг матрицы , система имеет единственное решение, т.е. является определённой.
Пример 2
Составим матрицы А и 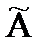, выполним эквивалентные преобразования:
, 
от матрицы А перешли к треугольной матрице, составляя линейные комбинации с элементами строк. Первую строку умножили на (-2) и сложили со второй строкой, затем вторую строку умножили на (-4) и сложили с третьей, первую умножили на (-3) и сложили с четвертой.
.
Отсюда видно, что r=3, =3, т.е. r= ; система совместна. Поскольку число n неизвестных также равно 3, то система является определённой.
Дата добавления: 2019-03-09; просмотров: 128; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!