РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МАТРИЧНЫМ МЕТОДОМ В Excel

Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования «Самарский государственный

Архитектурно строительный университет»

Белебеевский филиал университета

Республики Башкортостан.

Кафедра гуманитарных и естественнонаучных дисциплин

Решение систем алгебраических уравнений

Методические указания к практическим занятиям

 

Утверждены

 редакционно-издательским

советом университета

21 января 2008г.

Самара 2009

Составитель И.А.Попова

 УДК 517. 3(07)

Решение систем алгебраических уравнений: методические указания к практическим занятиям /сост. И.А. Попова; Самарск. гос. арх-строит. ун-т.-Самара 2009.- 23 с.

В методических указаниях приводятся методы Крамера и Гаусса решения систем алгебраических уравнений; примеры систем, имеющих единственное решение, множество решений. Предлагаются примеры для самостоятельного решения с целью закрепления данного материала. Имеется список основной литературы по теме.

Методические указания предназначены для студентов 1-го курса (1-2-го семестров обучения) специальностей ПГС (270102), ЭУС (080502).

Учебное издание

Редактор Л.Н. Конаныхина

Технический редактор А.И.Непогодина

Корректор Е.М. Исаева

 

 

Подписано в печать 20.12.08г. Формат 60*84 1/16 Бумага офсетная. Печать офсетная. Уч.-изд.л. 1,75. Усл.печ.л. 1,6. Тираж 100экз.

Самарский государственный архитектурно-строительный университет 443001 Самара, ул. Молодогвардейская, 194.

 

 

Самарский государственный

архитектурно строительный

университет, 2008

Общая часть

К системам алгебраических уравнений приводят многие задачи различных наук и их самых разнообразных прило­жений.

В естественных науках (физика, химия, биология, геоло­гия, география и др.) при обработке результатов наблю­дений часто встречаются со следующей задачей. Произве­дены измерения и получены значения одной величины (у) в зависимости от значений другой (х): зависимость вели­чины у от величины х может быть линейной, квадратичной или какой-нибудь иной, выражаемой соответственно фор­мулами у = ах + b , у = ах²+bx+c и т. п. Требуется найти коэффициенты соответствующей формулы.

Формулы, полученные при решении такого рода задач, называются эмпирическими. Значения коэффициентов эмпирической формулы находятся из системы n линейных уравнений с m неизвестными; коэффициенты этих уравне­ний соответствующим образом выражаются через резуль­таты измерений — значения x_i и y_i ; (i = 1, 2, .. ., n) рас­сматриваемых величин х и у.

К системам линейных уравнений приводят задачи геоде­зии, связанные с построением карт на основании данных геодезической съемки. Эти уравнения содержат большое число неизвестных. При составлении прогнозов погоды так­же приходится решать линейные системы со многими неиз­вестными.

Системы линейных уравнений широко используются в различных областях физики. К решению систем линейных уравнений сводятся задачи механики, связанные с расчётом фундаментов арок, мостов и других сооружений. В последние годы системы линейных уравнений находят широкое применение при решении технических, технологических и экономических задач.

Поэтому в данных методических указаниях разбираются основные методы решения систем линейных уравнений, в которых число уравнений не всегда совпадает с числом неизвестных. Рассматриваются примеры с решениями систем, приводятся необходимые пояснения и рекомендации. Данные методические указания помогут студентам очного и заочного отделений подготовиться к практическим занятиям по теме «Решение систем алгебраических уравнений». На последних страницах указаний имеется список используемой литературы, где более полно и подробно предоставлены теоретические положения темы.

ЛИНЕЙНЫЕ СИСТЕМЫ. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

Системой m линейных уравнений с n неизвестными x₁,x₂,…,x_n , или линейной системой, называется совокупность уравнений вида

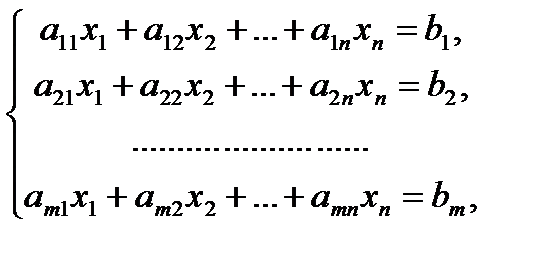                                                   (1)

где a_ik,b_i - заданные числа. Числа a_ik (i =1,2,…, m ; k =1,2,… n) называются коэффициентами, числа b _i (i=1, 2, ...,m) — свободными членами. Коэффициенты обозначены буквой a с двумя индексами i и k; первый индекс (i) указывает номер уравнения, второй индекс (k) — номер неизвестной, к которой относится данный коэффициент. Число m уравнений может быть больше, равно или меньше числа n неизвестных.

Линейная система называется неоднородной, если среди свободных членов имеются отличные от нуля. Если все сво­бодные члены равны нулю, то линейная система называется однородной. Однородная система имеет вид

                                               (2)

Решением линейной системы (1) называется упорядо­ченная совокупность m чисел

с₁,с₂,…,с_т, (с₁,с₂,…,с_т) ,                                                    (3)

подстановка которых вместо x₁, х₂, ..., х_n соответственно (x ₁ = с₁, x ₂₌ с₂, . .., х_n = с_n) обращает в тождество каж­дое из уравнений этой системы. Отметим, что числа (3) образуют одно решение.

Система, имеющая хотя бы одно решение, называется совместной, а система, не имеющая ни одного решения,— несовместной. Отметим, что однородная система (2) всегда совместна, так как она имеет нулевое решение: x₁=0, x₂= 0, ..., х_n = 0. Критерий совместимости линейной системы выражается следующей теоремой Кронекера-Капелли.

Теорема 1. Линейная система совместна тогда и только тогда, когда ранг матрицы системы равен рангу её расширенной матрицы.

Совместная система, имеющая единственное решение, называется определенной. Совместная система называется неопределенной, если она имеет более одного решения.

Две системы называются эквивалентными, или равно­сильными, если любое решение одной из них является так­же решением другой и обратно, т. е. если они имеют одно и то же множество решений. Любые две несовместные си­стемы считаются эквивалентными.

К элементарным преобразованиям линейной системы относятся следующие преобразования: 1) умножение уравнения системы на число, отличное от нуля; 2) прибав­ление к одному уравнению системы другого ее уравнения, умноженного на любое число; 3) перестановка местами двух уравнений системы.

Элементарными преобразованиями строк (столбцов) матрицы являются:

а) умножение i строки (столбца) матрицы на число ;

б) прибавление к i строке (столбцу)  строки (столбца), умноженной на число k;

в) перестановка i и  строк (столбцов) матрицы.

Матрица

,                                                              (4)

составленная из коэффициентов линейных уравнений системы (1), называется основной матрицей системы (или матрицей системы). Матрица

,                                                                      (5)

полученная присоединением к основной столбца из свободных членов, называется расширенной матрицей системы (1).

Рассмотрим столбцевые матрицы, составленные из неизвестных и свободных членов системы (1):

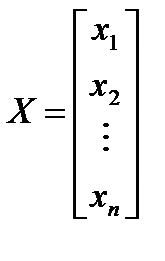, .                                                                (6)

Поскольку матрица А согласована с матрицей Х, то можно найти произведение

.

Элементами этой столбцевой матрицы являются левые части уравнений системы (1), поэтому на основании определения равенства матриц получаем

АХ=В.                                                                                    

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МАТРИЧНЫМ МЕТОДОМ В Excel

Пусть необходимо решить систему уравнений:

(7)

С использованием понятия матрицы и матричных операций система уравнений может быть записана в матричном виде:

А                         (8)

Здесь [А] - матрица коэффициентов системы вида:

 

             (9)

где 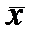,  - вектор неизвестных и вектор свободных членов соответственно.

Решение системы методом обратной матрицы может быть получено в результате умножения правой части системы уравнения (8) на матрицу, обратную к матрице коэффициентов системы:

.

Учитывая, что произведение обратной матрицы на прямую дает единичную матрицу, получаем

 или

Таким образом, решение системы сводится к нахождению обратной матрицы   А^-1 и затем вычислению произведения этой матрицы на вектор .

Этот метод удобно применять в тех случаях, когда несколько раз решается система с разными правыми частями. В этом случае достаточно один раз вычислить обратную матрицу ^-1 и затем умножать ее на разные векторы .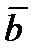

 

Пример 1

 

Методом обратной матрицы решить систему

Решение ищется в виде 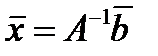. Вычислим обратную матрицу :

 

l) det = -25 + 3 = -22;

2)    3)

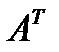 - транспортированная матрица;

4)

Теперь найдем вектор решения:

,

т.е. x₁ = 1; x₂ = 1.

Пример 2 Решить систему уравнений в Excel

Система уравнений имеет решение x₁ = 1, x₂ = 2, x₃ = 3. В матричной форме уравнения записываются следующим образом:

 

Для решения системы в Excel нужно:

1. Создать новый лист и присвоить ему имя «Система».

2. В ячейке А1 ввести Решение систем уравнений; обращение матрицы
(см.табл. 1).

3. В ячейку ВЗ ввести текст Ах = b . Теперь ввести матрицу коэффициентов
и вектор правой части b, для этого:

а) В ячейку А5 ввести «Исходная матрица ».

б) В ячейки А6:С8 ввести элементы матрицы :

 

Ячейка	Значение	Ячейка	Значение	Ячейка	Значение
А6	-8	В6	1	С6	2
А7	5	В7	7	С7	-3
А8	2	В8	1	С8	-2

 

в) Вячейку Е5 ввести «Правая часть (b)».

г) В ячейки Е6:Е8 ввести компоненты вектора правой части:

 

Ячейка	Значение	Ячейка	Значение	Ячейка	Значение
E6	0	E7	1	E8	-2

 

Таблица 1

	А	В	С	D	Е	F	G	Н
1	Решение систем уравнений. Обращение матрицы
2
3		Ах=b
4
5	Исходная матрица А				Правая часть (b)
6	-8	1	2		0
7	5	7	-3		10
8	2	1	-2		-2
9
10	Обратная матрица (1/А)				Вектор решения х=(1/А)/b
11	-0,149	0,054	-0,230		1
12	0,054	0,162	-0,189		2
13	-0,122	0,135	-0,824		3

Далее необходимо обратить матрицу А и умножить вектор  на матрицу, обратную к А. Применяемая для обращения матрицы функция МОБР возвращает массив значений, который вставляется сразу в целый столбец ячеек.

4. Для вычисления обратной матрицы нужно выполнить операции:

а) В ячейку А10 ввести текст «Обратная матрица (1/А)».

б) Выделить ячейки А11 :С13, куда будет помещена обратная матрица.

в) Щелкнуть по пиктограмме Мастер функций f

г) В первом окне Мастера функций выбрать категорию Математические ,
функцию МОБР.

д) Во втором окне Мастера функций ввести адрес массива исходной
матрицы А6:С8. Нажать одновременно клавиши Ctrl+ Shift+Enter для
вставки этой формулы во все выбранные ячейки А11 :С13.

5. Для умножения обратной матрицы на столбец свободных членов:

а) В ячейку Е10 ввести «Вектор решения х =(1/А)b»;

б) выделить ячейки Е11 :Е13;

в) щелкнуть по пиктограмме Мастер функций;

г) выбрать категорию Математические, функцию МУМНОЖ;

д) ввести формулу =МУМНОЖ(А11:С13; Е6:Е8);

е) затем нажать «Ctrl + Shift + Enter» для вставки формулы во все
выделенные ячейки.

Рабочий лист к этому моменту должен выглядеть так, как показано в табл.1 (режим показа формул - табл.2). В ячейках Е11-Е13 должны стоят значения компонентов вектора решения х₁ х₂, х₃ (в данном примере это числа (1;2;3)).

Используя табл. 1, методом обратных матриц решить систему уравнений, выбранную из табл. 3 по последней цифре шифра для индивидуального задания.

 

Таблица 2

 

	А	В	С	D	Е
1	Решение систем уравнений. Обращение матрицы
3		Ах=b
4
5	Исходная матрица А				Правая часть (b)
6	-8	1	2		0
7	5	7	-3		10
8	2	1	-2		-2
9
10	Обратная матрица (1/А)				Вектор решения х=(1/А)/b
11	=МОБР(А6:С8)	=МОБР(А6:С8)	=МОБР(А6:С8)		=МУМНОЖ(А11 :С13;Е6:Е8)
12	=МОБР(А6:С8)	=МОБР(А6:С8)	=МОБР(А6:С8)		=МУМНОЖ(А11 :С13;Е6:Е8)
13	=МОБР(А6:С8)	=МОБР(А6:С8)	=МОБР(А6:С8)		=МУМНОЖ(А11 :С13;Е6:Е8)

Пример 3 Решите системы линейных уравнений матричным методом
в Excel.

Таблица 3

 

№ вар.	Система линейных уравнений	№ вар.	Система линейных уравнений
№1		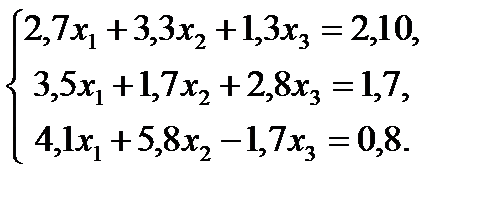№ 6
№2		№7
№3		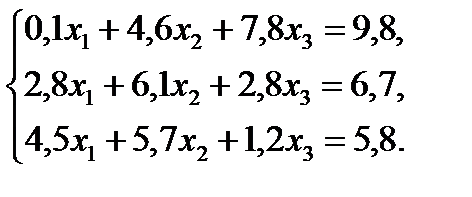№8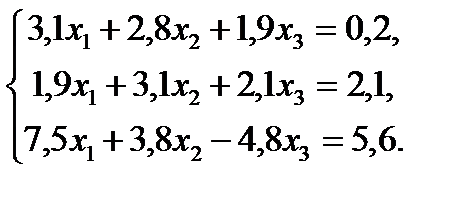
№4		№9
№5		№10

 

 

---

Дата добавления: 2019-03-09; просмотров: 301; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!