Связь между решениями неоднородной СЛУ и
Решениями ассоциированной с ней однородной СЛУ
Пусть дана НСЛУ


Тогда система


называется ассоциированной с системой  однородной системы линейных уравнений (ОСЛУ).
однородной системы линейных уравнений (ОСЛУ).
Обозначим через  множество всех решений ОСЛУ
множество всех решений ОСЛУ  , а через
, а через  - некоторое решение НСЛУ
- некоторое решение НСЛУ  .
.
Рассмотрим следующую сумму  , где
, где  (пробегает все
(пробегает все  ).
).
Теорема 1. Если решение НСЛУ  сложить с решением ОСЛУ
сложить с решением ОСЛУ  , то получится решение системы
, то получится решение системы  .
.
Доказательство. Пусть вектор  - решение НСЛУ
- решение НСЛУ  , а вектор
, а вектор  - решение ОСЛУ
- решение ОСЛУ  Значит,
Значит,
 ,
,  ,
, 
 ,
,  .
. 
Складывая  и
и  почленно, мы получим:
почленно, мы получим:
 .
. 
Из  следует: вектор
следует: вектор  является решением системы
является решением системы  . Теорема доказана.
. Теорема доказана.
Теорема 2. Разность разных двух решений НСЛУ  является решением ассоциированной с ней ОСЛУ
является решением ассоциированной с ней ОСЛУ  .
.
Доказательство. Пусть  и
и  - есть решение НСЛУ
- есть решение НСЛУ  . Тогда
. Тогда
 ,
,  ,
, 
 ,
,  .
. 
Вычитая из  выражение
выражение  , получим:
, получим:
 ,
,  .
. 
Из  имеем
имеем  - решение ОСЛУ
- решение ОСЛУ  . Теорема доказана.
. Теорема доказана.
Теорема 3. Если вектор  - решение НСЛУ
- решение НСЛУ  , а
, а  - множество всех решений ОСЛУ
- множество всех решений ОСЛУ  , то
, то 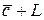 - множество всех решений НСЛУ
- множество всех решений НСЛУ  .
.
Следствие 1. Совместная НСЛУ  имеет единственное решение тогда и только тогда, когда ассоциированная с ней ОСЛУ
имеет единственное решение тогда и только тогда, когда ассоциированная с ней ОСЛУ  имеет единственное (нулевое) решение.
имеет единственное (нулевое) решение.
Следствие 2. Если две НСЛУ с неизвестными  совместны и равносильны, то ассоциированные с ними ОСЛУ равносильны.
совместны и равносильны, то ассоциированные с ними ОСЛУ равносильны.
|
|
|
Правило решения произвольной системы линейных уравнений
1. Найти ранги основной и расширенной матриц системы. Если  , то система несовместна.
, то система несовместна.
2. Если  , система совместна. Найти какой-либо базисный минор порядка
, система совместна. Найти какой-либо базисный минор порядка  (напоминание: минор, порядок которого определяет ранг матрицы, называется базисным). Взять
(напоминание: минор, порядок которого определяет ранг матрицы, называется базисным). Взять  уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называют главными и оставляют слева, а остальные
уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называют главными и оставляют слева, а остальные  неизвестных называют свободными и переносят в правые части уравнений.
неизвестных называют свободными и переносят в правые части уравнений.
3. Найти выражения главных неизвестных через свободные. Получено общее решение системы.
4. Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных. Таким образом, можно найти частные решения исходной системы уравнений.
Пример. Исследовать на совместность систему 
Решение: 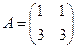 ,
,  ,
, 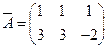 ,
,  ,
,
 .
.
Таким образом,  , следовательно, система несовместна.
, следовательно, система несовместна.
Пример. Решить систему  .
.
Решение:  . Берем два первых уравнения:
. Берем два первых уравнения:
 ,
,  ,
,
 ,
,  ,
, 
Следовательно,  ,
,  - общее решение. Положив, например,
- общее решение. Положив, например,  ,
,  , получаем одно из частных решений:
, получаем одно из частных решений:  ,
,  ,
,  ,
,  .
.
|
|
|
Дата добавления: 2019-02-26; просмотров: 1750; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
