Равенство строчного и столбцового рангов матрицы
Системы линейных уравнений
Основные понятия
Системой линейных алгебраических уравнений (СЛУ), содержащей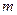 
уравнений и 
неизвестных, называется система вида
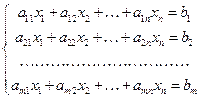
где числа 
, 
, 
называются коэффициентами системы, числа 
- свободными членами. Подлежат нахождению числа 
.
Такую систему удобно записывать в компактной матричной форме
.
Здесь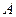 
- матрица коэффициентов системы, называемая основной матрицей:
,
- вектор-столбец из неизвестных 
,
- вектор-столбец из свободных членов .
Произведение матриц 
определено, так как в матрице 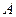столбцов столько же, сколько строк в матрице 
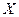( штук).
Расширенной матрицей системы называется матрица 
системы, дополненная столбцом свободных членов
.
Решением системы называется значений неизвестных 
, 
, 
, 
, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца
.
Система уравнений называется совместимой, если она имеет хотя бы одно решение, и несовместимой, если она не имеет ни одного решения.
Система
называется следствием системы , если каждое решение системы является также решением системы . Обозначается: 
.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.
|
|
|
Решить систему - это, значит, выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.
Две системы называются равносильными (эквивалентными, 
), если они имеют одно и то же общее решение.
Элементарными преобразованиями (э.п.) системы линейных уравнений (СЛУ) называются следующие преобразования:
1) умножение обеих частей какого-нибудь уравнения на скаляр, отличный от нуля;
2) прибавление (вычитание) к обеим частям какого-либо уравнения системы соответствующих частей другого уравнения системы, умноженных на скаляр;
3) исключение из системы или присоединение к ней линейного уравнения с нулевыми коэффициентами и нулевым свободным членом.
Теорема 1. Если одна СЛУ получается из другой СЛУ в результате цепочки э.п., то эти две системы равносильны.
Доказательство. Пусть дана СЛУ
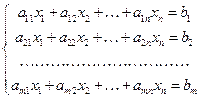
Получим из системы следующую
Ясно, что каждое решение системы есть также решение системы . Обратно: пусть вектор 
- любое решение системы . Тогда имеем:
|
|
|
Умножим первое равенство системы на скаляр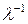 
и, не изменяя других равенств системы, получим равенство, показывающее, что вектор 
есть решение системы . Итак, системы и равносильны.
Легко проверить, что однократное применение к системе э.п. вида 1) и 2) приводит к системе, равносильной исходной системе .
Поскольку отношение равносильности транзитивно, то многократное применение э.п. приводит к системе уравнений, равносильной исходной системе . Теорема доказана.
Следствие 1. Если к одному из уравнений СЛУ прибавить линейную комбинацию других уравнений этой же системы, то получим систему уравнений, равносильную исходной.
Следствие 2. Если исключить из СЛУ или присоединить к ней уравнение, являющееся линейной комбинацией других уравнений этой системы, то получится СЛУ, равносильная исходной.
Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы.
Система линейных уравнений называется однородной если все свободные члены равны нулю:
Однородная система всегда совместна, так как 
является решением системы. Это решение называется нулевым или тривиальным.
|
|
|
Равенство строчного и столбцового рангов матрицы
Рассмотрим прямоугольную матрицу 
размерности 
:
Строки этой матрицы можно рассматривать как 
-мерные векторы, а столбцы – как 
-мерные векторы. Итак, матрицу можно рассматривать как систему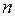 
-мерных векторов или систему -мерных векторов.
Строчечным рангом матрицы называется ранг системы ее строк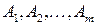 
(рассматриваем их как 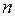-мерные векторы). Этот ранг будем обозначать через 
.
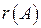Столбцовым рангом матрицы 
называется ранг системы ее столбцов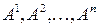 
(рассматриваем их как 
-мерные векторы). Этот ранг будем обозначать через 
.
Рассмотрим однородную систему линейных уравнений (ОСЛУ):
Матрица называется матрицей системы .
Теорема 1. Пусть система
состоит из первых 
уравнений системы .
Если ОСЛУ 
, то столбцовые ранги матриц этих систем равны.
Доказательство. Пусть и 
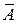- матрицы систем и соответственно. Положим, что 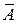- нулевая. Тогда любой вектор 
является решением системы , а значит, и решением системы . следовательно, матрица 
- также нулевая и ее ранг равен нулю.
|
|
|
Пусть теперь матрица 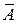- ненулевая и 
- базис системы ее столбцов. Но системы и равносильны, откуда система столбцов 
матрицы линейно независима. В самом деле: если число 
удовлетворяет неравенству 
, то система столбцов 
- линейно зависима, ибо в противном случае была бы независимость системы столбцов , чего быть не может.
Итак, 
- базис системы столбцов матрицы . Значит, столбцовый ранг матрицы 
.
Теорема 2. Строчечный ранг матрицы равен ее столбцовому рангу 
.
Доказательство. Для нулевой матрицы теорема очевидна. Пусть - ненулевая матрица и первые 
строк образуют базис системы строк этой системы.
Рассмотрим ОСЛУ, соответствующую матрице , т.е.
Рассмотрим также систему
которая состоит из первых 
строк системы ; ее матрицу обозначим через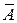 
. Т.к. первые строк матрицы образуют базис системы ее строк, то каждое уравнение системы есть линейная комбинация уравнений системы 
. Значит, системы и равносильны. Тогда по теореме 1 имеем:
Но столбцы матрицы 
есть -мерные векторы. Тогда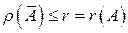 
. Значит, в силу 
имеем:
Аналогичное неравенство имеем для транспонированной матрицы 
:
Но 
, 
. Из 
следует:
Из 
и 
следует 
. Теорема доказана.
Решение СЛУ методом Гаусса
Одним из наиболее универсальных и эффективных методов решений линейных алгебраических систем является метод Гаусса, состоящий в последовательном исключении неизвестных.
Пусть дана система уравнений
Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.
Приведенная ниже система имеет ступенчатый вид
где 
, 
. Коэффициенты 
называются главными элементами системы.
На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы. Опишем метод Гаусса подробнее.
Прямой ход.
Будем считать, что элемент 
(если 
, то первым в системе запишем уравнение, в котором коэффициент при 
отличен от нуля).
Преобразуем систему 
, исключив неизвестное во всех уравнениях, кроме первого (используя элементарные преобразования системы). Для этого умножим обе части первого уравнения на 
и сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения на 
и сложим с третьим уравнением системы. Продолжая этот процесс, получим эквивалентную систему
Здесь 
, 
, 
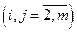- новые значения коэффициентов и правых частей, которые получаются после первого шага.
Аналогичным образом, считая главным элементом 
, исключим неизвестное 
из всех уравнений системы, кроме первого и второго, и так далее. Продолжаем этот процесс, пока это возможно.
Если в процессе приведения системы к ступенчатому виду появятся нулевые уравнения, т. е. равенства вида 
, их отбрасывают. Если же появится уравнение вида 
, а 
, то это свидетельствует о несовместности системы.
Второй этап (обратный ход) заключается в решении ступенчатой системы. Ступенчатая система уравнений, вообще говоря, имеет бесчисленное множество решений. В последнем уравнении этой системы выражаем первое неизвестное 
через остальные неизвестные 
. Затем подставляем значение 
в предпоследнее уравнение системы и выражаем 
через ; затем находим 
. Придавая свободным неизвестным произвольные значения, получим бесчисленное множество решений системы.
Замечание 1. Если ступенчатая система оказывается треугольной, т.е. 
, то исходная система имеет единственное решение. Из последнего уравнения находим 
, из предпоследнего уравнения 
, далее поднимаясь по системе вверх, найдем все остальные неизвестные 
.
Замечание 2. На практике удобнее работать не с системой , а с расширенной ее матрицей, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент 
был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на 
).
Пример. Решить систему методом Гаусса:
Решение: В результате элементарных преобразований над расширенной матрицей системы
исходная система свелась к ступенчатой:
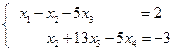
Поэтому общее решение системы: 
, 
. Если положить, например, 
, 
, то найдем одно из частных решений этой системы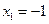 
, 
, , .
Пример. Решить систему методом Гаусса:
Решение: Произведем элементарные преобразования над строчками расширенной матрицы системы:
.
Полученная матрица соответствует системе
Осуществляя обратный ход, находим 
, 
, 
.
Дата добавления: 2019-02-26; просмотров: 4272; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!