Уравнения движения самолета в скалярной форме.
Глава 1. Динамика полета
Уравнения движения самолета
Уравнения движения в векторной форме.
Реальный самолет представляет собой сложную упругую механическую систему с жидким наполнением. В соответствии с правилами механики движение такой системы можно представить двумя векторными уравнениями, первое из которых описывает поступательное движение центра масс самолета относительно инерциальной системы координат, а второе – вращательное движение самолета как твердого тела относительно своего центра масс:
; 
(1.1)
Где, m – масса самолета;
– вектор скорости центра масс;
– результирующий вектор внешних сил, действующих на самолет (аэродинамических, тяги двигателей, тяжести);
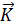– результирующий вектор момента количества движения самолета относительно центра масс;
–результирующий вектор моментов внешних сил относительно центра масс.
Основные системы координат.
Основными системами координат, принятыми в динамике полета, являются нормальная земная, нормальная связанная, скоростная и траекторная.
Для рассмотрения силового воздействия между самолетом и воздушной средой приняты скоростная и связанная системы координат. Начало этих прямоугольных, правых, подвижным систем координат помещается в центре масс самолета, обычно расположенном в плоскости симметрии самолета OXY (рис 1.1)
Рис 1.1 Связанная и скоростная системы координат
|
|
|
Продольная ось OXсвязанной системы координат OXYZ лежит в плоскости симметрии самолета и направлена от хвостовой части самолета кносовой параллельно средней аэродинамической хорде (CAX) крыла или строительной горизонтали фюзеляжа.
Нормальная ось OYсвязанной системы координат находится в плоскости симметрии и направлена к верхней поверхности крыла.
Поперечная ось OZ перпендикулярна плоскости симметрии самолета и направлена в сторону правого полукрыла.
Скоростная ось OXaYZa совпадает с направлением скорости самолета относительно воздушной среды 
.
Ось подъемной силы OYa лежит в плоскости симметрии самолета и направлена к верхней части самолета.
Боковая осьOZa нормальная к плоскостиOXaYa и направлена в сторону правого полукрыла.
Связанная система координат неподвижна относительно самолета, а скоростная система координат поворачивается, «следя» за вектором скорости полета . Положение самолета относительно вектора скорости (или набегающего воздушного потока) отпределяется углами атаки α и скольжения β.
Нормальная земная система координат OoXgYgZg(рис. 1.2) неподвижно связана с Землей и считается инерционной. Начало координат выбирается в соответствии с рассматриваемой задачей на поверхности земли (точка Oo).
|
|
|
Ось OoYgнаправлена вверх по местной вертикали, оси OoXg и OoZgлежат в плоскости местного горизонта OoXgZg(в горизонтальной плоскости). Плоскость OoXgYg называется вертикальной.
Положение самолета относительно нормальной земной системы координат определяется тремя координатами Xg, Yg,Zgцентра масс О самолета. Скорость движения центра масс самолета относительно земной системы координат называется земной скоростью k.
Рис 1.2 Нормальная земная OoXgYgZgи связанная OXYZ системы координат;
Xg, Yg,Zg– координаты центра масс самолета в нормальной земной системе координат
Нормальная система координат OoXgYgZg(рис. 1.3) – подвижная система координат, начало которой помещено в центре масс самолета, ось OYgнаправлена по местной вертикали, а направление осей OoXg и OZgвыбирается в соответствии с задачей, например параллельно соответствующим осям нормальной земной системы координат.
Рис. 1.3 взаимное расположение связаннойOXYZ и нормальнойOoXgYgZgсистем координат
Положение связанной системы координат OXYZ относительно нормальной системы координат OXgYgZg определяется углами φ, θ, γ.
|
|
|
Угол рыскания φ – это угол между осью OXgнормальной системы координат и проекции продольной оси OX на горизонтальную плоскость OXgZg.
Угол тангажаθ – угол между продольной осью OX и горизонтальной плоскостью OXgZg нормальной системы координат.
Угол крена γ – это угол между поперечной осью OZ и осью OZgнормальной системы координат, смещенной в положение, при котором угол рыскания равен нулю, или, что то же самое, угол, заключенный между нормальной осью OY и вертикальной плоскостью, содержащей продольную ось OX.
Траекторная система координат OXkYkZk(рис. 1.4) – это подвижная система координат, начало которой лежит в центре масс самолета. Ось OXkнаправлена по вектору земной скорости самолета Vk. Ось OYk лежит в вертикальной плоскости, проходящей через ось OXk и направлена обычно вверх от поверхности земли. Ось OZkобразует с осями OXk и OYkправую систему координат. Положение траекторной системы координат относительно нормальной системы координат определяется двумя траекторными углами θ и φ. Угол θ между горизонтальной плоскостью OXgZgи вектором земной скорости kназывается УГЛОМ НАКЛОНА ТРАЕКТОРИИ. Угол φ между осьюOXg нормальной системы координат и направлением путевой скорости пназывается ПУТЕВЫМ.
|
|
|
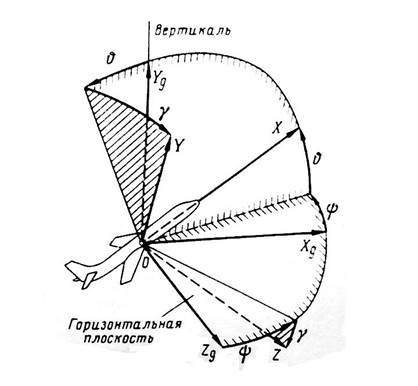
Рис. 1.4 Взаимное положение нормальной OXgYgZgи траекторной OXkYkZkсистем координат.
Путевой скоростью пназывается проекция земной скорости kсамолета на горизонтальную плоскость OXgZgнормальной системы координат. Так как направление оси OXg задается исходя из условия задачи, то приφ=0 путевая скорость псовпадает с осью OXg. Она называется ГОРИЗОНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ СКОРОСТИ x.
Проекция земной скорости kна ось OYgназывается ВЕРТИКАЛЬНОЙ СОСТАВЛЯЮЩЕЙ СКОРОСТИ kили вертикальной скоростью и обозначается y. Если ветер отсутствует и γ=0, то скоростная и траекторная системы координат совпадают.
Уравнения движения самолета в скалярной форме.
Пространственное движение самолета для удобства изучения представляется в виде двух независимых движений: в вертикальной плоскости и в горизонтальной. Каждое из движений, в свою очередь, представляется совокупностью поступательного движения центра масс и вращательного относительно центра масс, которые считаются так же независимыми.
Движение самолета в плоскости симметрии OXYZ называется продольным движением самолета. Оно включает поступательное движение центра масс вдоль осей OXkиOYk и вращательное движение относительно оси OZ. Движение самолета в вертикальной плоскости является частным случаем продольного движения самолета. Система уравнений движения самолета в вертикальной плоскости имеет вид:
; 
;
; 
;
; 
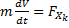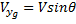(1.2)
; 
; 
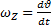Где Ik– момент инерции самолета относительноOZ.
Первые два уравнения – динамические уравнения движения центра масс, третье – динамическое уравнение движения относительно оси OZ, остальные – кинематические уравнения.
Движение самолета в плоскости OXZ, перпендикулярной плоскости симметрии самолета, называется БОКОВЫМ. Оно включает поступательное движение центра масс вдоль оси OZkи вращательные движения относительно осей OY и OZ. Движение самолета горизонтальной плоскости является частным случаем бокового движения. Система динамических уравнений движения самолета в горизонтальной плоскости имеет вид:
; 
;
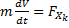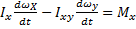; (1.3)
.
Где IxиIy– осевые моменты самолета,
IxyиIyx– центробежные моменты самолета относительно осей связанной системы координат.
Системы уравнений (1.3) и (1.2) позволяют исследовать опорное (невозмущенное) поступательное и вращательное движение самолета в вертикальной и горизонтальной плоскости соответственно.
Методы решения задач динамики полета.
Системы уравнений движения летательного аппарата позволяет ответить на любой вопрос, касающийся траектории полета, характера возмущенного движения, характеристик устойчивости и управляемости. Однако решение систем дифференциальных уравнений представляет значительные сложности. Для упрощения решения уравнений в математике и механике разработаны методы упрощения.
Способы решения систем дифференциальных уравнений в аналитическом виде до сих пор не разработаны, поэтому используются методы численного интегрирования с помощью счетно-решающих устройств, а также приближенные методы решения, позволяющие определить с известной точностью численные значения параметров движения.
Распространенным считается метод математического моделирования, суть которых сводится к тому, что различные по своей физической природе явления могут описываться одними и теми же тождественными уравнениями.
Если самолет устойчив, заданы условия полета, известны возмущающие и управляющие воздействия, то при заданных начальных условиях решение уравнений позволяет однозначно определить изменение во времени всех переменных, характеризующих движение. Решение уравнений движения в этом случае называют прямой задачей анализа.
В реальном полете задаются требуемые параметры движения: высота, скорость, курс. Пилот формирует управляющие воздействия таким образом, чтобы обеспечить требуемые параметры движения и парировать их отклонения от заданных, выбирая для этого в каждый момент времени соответствующие отклонения органов управления. Эту же задачу решает автопилот в соответствии с заложенным в него законом управления.
Дата добавления: 2019-02-26; просмотров: 1120; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!